Коллективы решающих правил
Давно известны приемы повышения качества принимаемых решений, состоящие в объединении специалистов той или иной области знаний в коллектив, вырабатывающий совместное решение. Идею коллективного решения можно применить и к "коллективу" формальных алгоритмов, что позволит повысить эффективность решения многих задач.
Для рационального использования особенностей различных алгоритмов при решении задач распознавания возможно объединить различные по характеру алгоритмы распознавания в коллективы, которые формируют классификационное решение на основе правил, принятых в теории коллективных решений. Пусть в некоторой ситуации Х принимается решение S. Тогда S=R(X), где R — алгоритм принятия решения в ситуации X. Предположим, что существует L различных алгоритмов решения задачи, т. е. Sl=Rl(X), l=1, 2, ... , L, где Sl — решение, полученное алгоритмом Rl. Будем называть множество алгоритмов {R}={R1, R2, ..., Ri.} коллективом алгоритмов решения задачи (коллективом решающих правил), если на множестве решений Sl в любой ситуации Х определено решающее правило F, т. е. S=F(S1, S2, ..., SL, X). Алгоритмы Rl принято называть членами коллектива, Sl — решением l-го члена коллектива, а S — коллективным решением. Функция F определяет способ обобщения индивидуальных решений в решения коллектива S. Поэтому синтез функции F, или способ обобщения, является центральным моментом в организации коллектива.
Принятие коллективного решения может быть использовано при решении различных задач. Так, в задаче управления под ситуацией понимается ситуация среды и целей управления, а под решением — самоуправление, приводящее объект в целевое состояние. В задачах прогноза Х — исходное, а S — прогнозируемое состояние. В задачах распознавания ситуацией Х является описание объекта X, т. е. его изображение, а решением S — номер образа, к которому принадлежит наблюдаемое изображение. Индивидуальное и коллективное решения в задаче распознавания состоят в отнесении некоторого изображения к одному из образов. Наиболее интересными коллективами распознающих алгоритмов являются такие, в которых существует зависимость веса каждого решающего правила Rl от распознаваемого изображения. Например, вес решающего правила Rl может определяться соотношением

| (57) |
где Bl — область компетентности решающего правила Rl. Веса решающих правил выбираются так, что
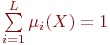
| (58) |
для всех возможных значений X. Соотношение (57) означает, что решение коллектива определяется решением того решающего правила Ri, области компетентности которого принадлежит изображение объекта X. Такой подход представляет собой двухуровневую процедуру распознавания. На первом уровне определяется принадлежность изображения той или иной области компетентности, а уже на втором — вступает в силу решающее правило, компетентность которого максимальна в найденной области. Решение этого правила отождествляется с решением всего коллектива. Основным этапом в такой организации коллективного решения является обучение распознаванию областей компетентности. Практически постановкой этой задачи различаются правила организации решения коллектива. Области компетентности можно искать, используя вероятностные свойства правил коллектива, можно применить гипотезу компактности и считать, что одинаковым правилам должны соответствовать компактные области, которые можно выделить алгоритмами самообучения. В процессе обучения сначала выделяются компактные множества и соответствующие им области, а затем в каждой из этих областей восстанавливается свое решающее правило. Решение такого правила, действующего в определенной области, объявляется диктаторским, т. е. отождествляется с решением всего коллектива.
В персептроне каждый A-элемент может интерпретироваться как член коллектива. В процессе обучения все A-элементы приобретают веса, в соответствии с которыми эти A-элементы участвуют в коллективном решении. Особенность каждого A-элемента состоит в том, что он действует в некотором подпространстве исходного пространства, характер которого определяется связями между S- и A-элементами. Решение, получаемое на выходе персептрона, можно интерпретировать как средневзвешенное решение коллектива, состоящего из всех A-элементов.
Контрольные вопросы:
1. Опишите модель нейронной сети с обратным распространением ошибки.
2. Что представляет собой многослойная структура нейронной сети?
3. В чем заключается обучение сети без учителя?
4. Опишите схему сети Хопфилда.
5. В чем заключается метод потенциальных функций?
6. В чем заключается метод группового учета аргументов МГУА?
Основная литература
1. Матвеев, М.Г. Модели и методы искусственного интеллекта. Применение в экономике: уч. пособие/ М.Г.Матвеев, А.С.Свиридов. и др.- М.: Финансы и статистика; ИНФРА-М, 2008.- 448с
2. Информационные системы в экономике: учеб. пособ./под ред. А.Н. Романова, Б.Б. Одинцова, - М.: Вузовский учебник, 2008. – 411 с.
3. Ездаков, А.Л. Функциональное и логическое программирование: учеб. пособие.- М.: БИНОМ; Лаборатория знаний, 2009.-119с.
Дополнительная литература
1. Матвеев, М.Г. Модели и методы искусственного интеллекта. Применение в экономике: уч. пособие/ М.Г.Матвеев, А.С.Свиридов. и др.- М.: Финансы и статистика; ИНФРА-М, 2008.- 448с
2. Информационные системы в экономике: учеб. пособ./под ред. А.Н. Романова, Б.Б. Одинцова, - М.: Вузовский учебник, 2008. – 411 с.
3. Ездаков, А.Л. Функциональное и логическое программирование: учеб. пособие.- М.: БИНОМ; Лаборатория знаний, 2009.-119с.
4. Арсеньев С.Н., Шелобов СИ., Давыдова Т.Ю. Принятие решений. Интегрированные информационные системы. Учебное пособие для вузов. -М: ЮНИТИ-ДАНА, 2003.
5. Джексон П. Введение в экспертные системы / Учебное пособие. - М.: «Вильямс», 2001
6. Винер Н. Кибернетика или управление и связь в животном и машине. - М.: Наука, 1981.
7. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. - М.: Мир, 1976.
8. Искусственный интеллект. Под ред. Д.А.Поспелова. - М.: Радио и связь, 1990.
9. Пенроуз Р. Новый ум короля: о компьютерах, мышлении и законах физики. М.: Издательство ЛКИ, 2007.
10. Смолин Д.В. Введение в искусственный интеллект: конспект лекций. М.- ФИЗМАЛИТ, 2004.
11. Андрейчиков А.В., Андрейчикова О.Н. Интеллектуальные информационные системы. Финансы и статистика- М: 2004.
12. Леденева Т.М., Подвальный С.Л. Системы искусственного интеллекта и принятие решений; Учебное пособие; Уфа: УГАТУ, 2005.
13. Горбань А.Н. Обучение нейронных сетей. - М.: СИ Параграф, 2006.
14. Девятков В.В. Системы искусственного интеллекта. - М.: Изд-во МГТУ им. Баумана, 2007.
15. Лорьер Ж.-Л. Системы искусственного интеллекта. - М, Мир, 2005.
Дата добавления: 2015-02-28; просмотров: 1142;
