Алгоритм с ковариациями и с квадратичными описаниями

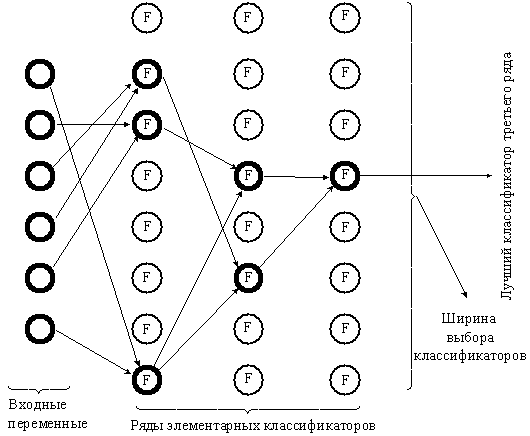
Рис 8. МГУА как эквивалент массовой селекции

В этом алгоритме [5, 6] используются частные описания, представленные в следующих формулах: y_i=a₀+a₁x_i+a₂x_j+a₃x_ix_j; .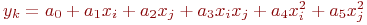

Сложность модели увеличивается от ряда к ряду селекции как по числу учитываемых аргументов, так и по степени. Степень полного описания быстро растет. На первом ряду — квадратичные описания, на втором — четвертой степени, на третьем — восьмой и т. д. В связи с этим минимум критерия селекции находится быстро, но не совсем точно. Кроме того, имеется опасность потери существенного аргумента, особенно на первых рядах селекции (в случае отсутствия протекции). Специальные теоремы теории МГУА определяют условия, при которых результат селекции не отличается от результата полного перебора моделей.

Чтобы степень полного уравнения повышалась с каждым рядом селекции на единицу, достаточно рассматривать все аргументы и их ковариации как обобщенные аргументы и пользоваться составленными для них линейными описаниями.

Метод предельных упрощений (МПУ)

По тому, как организован процесс обучения распознающих систем, четко выделяются два подхода к проблеме ОРО. Первый основан на построении сложных разделяющих поверхностей в случайно выбранных пространствах, а во втором центр тяжести проблемы переносится на достижение понимания принципов формирования такого описания объектов, в рамках которого сам процесс распознавания чрезвычайно прост. Обучение в этом случае рассматривается как некий процесс конструирования пространств для решения конкретных задач.

В МПУ предполагается, что разделяющая функция задается заранее в виде линейного (самого простого) полинома, а процесс обучения состоит в конструировании такого пространства минимальной размерности, в котором заранее заданная наиболее простая разделяющая функция безошибочно разделяет обучающую последовательность. МПР назван так потому, что в нем строится самое простое решающее правило в пространстве небольшой размерности, т. е. в простом пространстве.

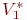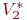Пусть на некотором множестве объектов V заданы два подмножества и , определяющие собой образы на обучающей последовательности V. Рассмотрим i-е свойство объектов, такое, что некоторые объекты обучающей последовательности этим свойством обладают, а другие — нет. Пусть заданным свойством обладают объекты, образующие подмножество V_1i, а объекты подмножества V_2i этим свойством не обладают ( 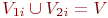). Тогда i-е свойство называют признаком первого типа относительно образа 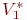, если выполняются соотношения

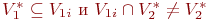
(50)

и признаком второго типа, если выполняются

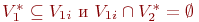
(51)

Если же выполняются соотношения

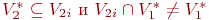
(52)

то i-е свойство считается признаком первого типа относительно образа 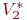, а если выполняются

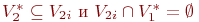
(53)

то это же свойство объявляется признаком второго типа относительно образа 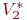. Если свойство не обладает ни одной из приведенных особенностей, то оно вообще не относится к признакам и не участвует в формировании пространства.

Одинаковые признаки — это два признака x_i и x_j, порождающие подмножества V_1j, V_2j, V_1i, V_2i, такие, что

V_1j= V_1i и V_2j= V_2i. (4.54)

Доказано утверждение, смысл которого заключается в том, что если пространство конструировать из однотипных, но неодинаковых признаков, то в конце концов будет построено такое пространство, в котором обучающая последовательность будет безошибочно разделена на два образа линейным, т. е. самым простым, решающим правилом.

Метод предельных упрощений состоит в том, что в процессе обучения последовательно проверяются все возможные свойства объектов и из них выбираются только такие, которые обладают хотя бы одной из особенностей, определяемых соотношениями (4.50), (4.51). Такой отбор однотипных, но неодинаковых признаков продолжается до тех пор, пока при некотором значении размерности пространства не наступит безошибочное линейное разделение образов на обучающей последовательности. В зависимости от того, из признаков какого типа строится пространство, в качестве разделяющей плоскости выбирается плоскость, описываемая уравнением

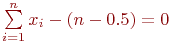
(55)

либо уравнением

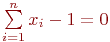
(56)

Каждый объект относится к одному из образов в зависимости от того, по какую сторону относительно плоскости находится соответствующий этому объекту вектор в пространстве признаков размерности n.