Понятие о фермах
При перекрытии больших пролетов (мосты, промышленные здания и т.п.) и в крупных строительных кранах часто применяются конструкции, называемые фермами.
Фермой называется жесткая конструкция, состоящая из стержней, соединенных на концах шарнирами. Шарнирные соединения стержней фермы называются ее узлами.
Фермы бывают двух основных видов: 1)без лишних стержней (рис.7.4); 2)с лишними стержнями (рис.7.5.).
 | |||
 | |||
Рис.7.4. Рис.7.5.
Обозначим через n-число узлов фермы, через m-число стержней. Чтобы ферма была без лишних стержней, должна выполняться зависимость:
m=2n-3.
Если m<2n-3, имеем изменяемую систему.
Если m>2n-3, имеем ферму с лишними стержнями.
При инженерных расчетах фермы обычно исходят из следующих упрощающих предположений:
1)все стержни фермы прямолинейны;
2)трение в шарнирах отсутствует;
3)все нагрузки лежат в плоскости фермы и приложены в узлах;
4)весом стержней пренебрегают.
При выполнении этих условий каждый стержень испытывает только сжатие или растяжение и не испытывает изгиба.
Расчет ферм сводится к определению опорных реакций и усилий в ее стержнях. Заданные силы и опорные реакции считаются внешними силами, усилия в стержнях - внутренними.
Фермы различают статически определимые и статически неопределимые. Если опорные реакции и усилия в стержнях могут быть определены методами статики твердого тела, то ферма является статически определимой, в противном случае - ферма статически неопределима. Все фермы без лишних стержней - статически определимы. Рассмотрим следующие способы определения усилий в стержнях статически определимых ферм:
1)способ вырезания узлов;
2)способ разрезов фермы (способ Риттера).
Способ вырезания узлов
Этим способом удобно пользоваться, когда надо найти усилия во всех стержнях фермы, при этом задачу можно решать графически, и аналитически. Графически способ значительно проще, нагляднее, но менее точен.
а)графическое решение. Сущность этого способа поясним на следующей конкретной задаче. По заданным активным силам P1=4 кН, Р2=2 кН определить реакции опор RA, RB и усилия S1, S2, S3, S4, S5 в стержнях фермы, изображенной на рис.7.6.

Рис.7.6.
Реакции опор RA и RB определяем с помощью силового и веревочного многоугольника, как это было сделано для балки, изображенной на рис.7.3. Для определения усилий в стержнях фермы надо последовательно вырезать каждый из узлов фермы, причем перерезанные стержни заменять их реакциями, которые численно равны усилиям в стержнях. Поскольку узлы фермы находятся в равновесии, то силовые многоугольники, построенные для сил, сходящихся в каждом узле, должны быть замкнутыми.
Начинать надо вырезать с такого узла, где сходится только два стержня. Силовые многоугольники строятся в определенном масштабе, причем построение надо начинать с известных сил. Обходя полученный многоугольник по периметру в направлении известной силы, определяем направление искомых сил. Модули их определяются непосредственным измерением. При этом следует помнить, что реакции каждого стержня, приложенные к узлам, которые он соединяет, всегда равны по модулю и противоположны по направлению. Характер усилий в стержнях фермы определяется по следующему правилу: если реакция данного стержня, приложенная к вырезанному узлу, направлена к этому узлу, то стержень сжат, если же эта реакция направления от узла, то стержень растянут.
Силовые многоугольники для узлов А,В,С показаны на рис.7.7.(Узел D нет необходимости вырезать, т.к. все усилия в стержнях, сходящихся в этом узле, уже определены ).

Рис.7.7.
в)Аналитическое решение для фермы, изображенной на рис.7.6.
Вначале определяем опорные реакции RA и RB, считая ферму геометрически неизменяемой системой и составляя уравнения равновесия плоской системы сил. (Учитываются только внешние силы, действующие на ферму).
åmA( 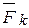 )=0 RB×4-P2 ×2-P1×1=0
)=0 RB×4-P2 ×2-P1×1=0
åmB( 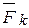 )=0 -RA×4+P1 ×3+P2×2=0
)=0 -RA×4+P1 ×3+P2×2=0
Отсюда
RB= 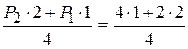 =2 кН
=2 кН
RA= 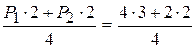 =4 кН
=4 кН
Затем начинаем поочередно вырезать узлы, причем первым вырезаем тот узел, где сходится не более двух стержней. Перерезанные стержни заменяем их реакциями, которые направляем от узлов, считая стержни растянутыми. Каждый раз будем иметь сходящуюся плоскую систему сил, для которой составляются уравнения равновесия:
åFkx=0
åFky=0
Решаем эти уравнения и определяем неизвестные величины, причем, если значение усилия в каком-либо стержне получится отрицательным, то это будет означать, что данный стержень не растянут, а сжат.
Выполним подробно эти расчеты:
1)Узел А

åFkx=0 S1×cos600+S2=0
åFky=0 RA+S1×cos300=0
Отсюда
S1=- 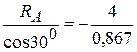 =-4,6 кН
=-4,6 кН
S2=-S1×cos600=4,6×0,5=2,3 кН
2)Узел В

åFkx=0 -S5×cos300 - S4=0
åFky=0 RB + S5×cos600=0
Отсюда
S5=- 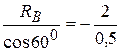 =-4 кН
=-4 кН
S4=-S5×cos300=4×0,867=3,47 кН.
3)Узел С

Для определения последнего неизвестного усилия S3 здесь достаточно составить одно уравнение равновесия:
åFky=0 S3 ×cos300 - P2=0
Отсюда
S3= 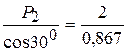 =2,3 кН.
=2,3 кН.
Из полученных ответов видно, что стержни S1, S5 сжаты под действием заданной нагрузки, остальные стержни - растянуты.
Дата добавления: 2015-02-25; просмотров: 1354;
