Способ разрезов фермы

Этим способом удобно пользоваться для определения усилий в отдельных стержнях фермы. Идея этого способа заключается в следующем:

1)Также, как и при способе вырезания узлов, здесь вначале определяются опорные реакции, для чего составляются три уравнения равновесия для всей фермы в целом, учитывая только заданные нагрузки и опорные реакции.

2)Разрезают ферму на 2 части, при этом первый разрез делают не более, чем по трем стержням. Мысленно удаляют одну часть фермы, а в оставшейся части реакцию каждого перерезанного стержня направляют вдоль этого стержня от узла.

3)Составляют для оставшейся части три уравнения равновесия: три уравнения моментов относительно трех точек, в которых попарно пересекаются направления перерезанных стержней; если из перерезанных стержней два параллельны, то вместо третьего уравнения моментов составляют уравнение проекций на ось, перпендикулярную параллельным стержням.

4)Из этих уравнений равновесия определяют реакции (усилия) перерезанных стержней;

5)Далее, производя другие разрезы по различным стержням, определяют таким же образом усилия во всех стержнях фермы.

Поясним сказанное на примере фермы, изображенной на рис.7.6. Пусть, например, требуется определить здесь усилия в стержнях 2, 3, 5. Так как опорные реакции 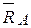, 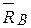уже были ранее найдены, то делаем сразу разрез 1-1 по этим стержням и рассмотрим равновесие правой части. Составляем три уравнения равновесия:

åm_B( 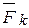)=0 P₂×2-S₃×cos30⁰×2=0

åm_C( 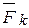)=0 R_B×2+S₅×cos60⁰×2=0

åm_D( 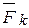)=0 R_B×3-P₂×1-S₂×1×tg60⁰=0

Отсюда

S₃= 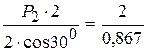=2,3 кН

S₅=- 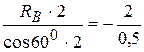=-4 кН

S₂= 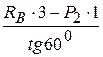= =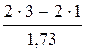2,3 кН.

Вопросы для самопроверки

1.Что называется графостатикой?

2.Как графически находится равнодействующая плоской системы сил?

3.Что такое силовой и веревочный многоугольники?

4.Каковы графические условия равновесия плоской системы сил?

5.Как графически определяются опорные реакции?

6.Какую конструкцию называют фермой?

7.Какие допущения делаются при расчете ферм?

8.Объясните, почему при этих допущениях стержни работают только на сжатие или растяжение?

9.Как связано число стержней с количеством узлов у статически определимой фермы?

10.Как определить сжат или растянут данный стержень фермы?

11.В чем заключается способ вырезания узлов при аналитическом решении?

12.В чем заключается способ вырезания узлов при графическом решении?

13.В чем заключается способ разрезов фермы (способ Риттера)?

ЗАДАЧИ

I. Определить опорные реакции и усилия в стержнях 2,5,9,10 навесной фермы, изображенной вместе с действующими на нее силами на рис.7.9., если P₁=1 кН, Р₂=2 кН, Р₃=2 кН, Р₄=1 кН.

Рис.7.9.

Решение. Определяем сначала опорные реакции X_A, Y_A, R_B, рассматривая равновесие всей фермы.

Составим три уравнения равновесия плоской системы сил

åF_kx=0 X_A- R_B=0

åF_ky=0 Y_A- P₁- P₂ - P₃ - P₄=0

åm_A( 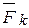)=0 R_B×7,5- P₂×4,5 - P₃×9 - P₄×13,5=0

Отсюда

R_B= 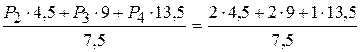=5,4 кН

X_A=R_B=5,4 кН

Y_A=P₁+P₂+P₃+P₄=1+2+2+1=6 кН.

Далее определим искомые усилия в стержнях фермы методом Риттера. Для этого делаем первый разрез 1-1 по стержням 5,10,2 и рассматриваем равновесие правой части фермы. Реакции перерезанных стержней обозначим 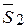, , 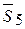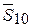. Составим следующие уравнения равновесия:

åm_C( 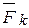)=0 P₃×4,5- S₁₀×sinb ×4,5=0

åm_M( 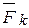)=0 -P₄×9- P₃×4,5-S₂ ×5=0

åm_E( 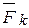)=0 -P₄×4,5+ S₅×cosa ×2,5=0

Определяем неизвестные cosa и sinb.

cosa= 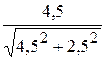=0,874 sinb= 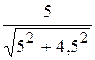=0,743

Тогда

S₁₀= 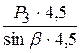= =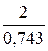2,7 кН

S₅= 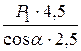= =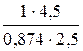2,06 кН

S₂= 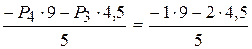=3,6 кН.

Для определения оставшегося искомого усилия S₉ делаем второй разрез II-II по стержням 6,9,2; опять рассматриваем равновесие правой части фермы. Составим только одно уравнение равновесия.

åm_C( 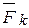)=0 S₉×9+ P₂×9+P₃ ×4,5=0

Отсюда

S₉= 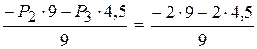=-3 кН.

<29 30 313233 34 35 >

Дата добавления: 2015-02-25; просмотров: 1010;