Определение средней арифметической взвешенной по интервальному ряду
Сначала находят центры (середины) интервалов, а затем их умножают на веса, произведения суммируют и делят на сумму весов.
Пример. Требуется определить среднемесячную заработную плату одного рабочего по следующим данным (табл. 4.2)
Таблица 4.2 – Исходные данные:
| Исходные данные: | Расчетные данные: | ||
| месячная зарплата, руб. | Число рабочих, чел. | Середины интервалов | - |
| xi | fi | 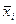
| 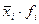
|
| 4000-5000 | |||
| 5000-6000 | |||
| 6000-7000 | |||
| 7000-8000 | |||
| 8000-9000 | |||
| 9000-10000 | |||
| Итого | - |
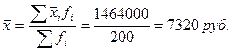
Средняя арифметическая обладает рядом полезных свойств, к важнейшим из которых относятся:
1. Средняя арифметическая постоянной величины равна этой величине:
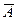 = А при А=const;
= А при А=const;
2 . Алгебраическая сумма отклонений вариант от их средней арифметической равна нулю:
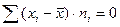 (4.13)
(4.13)
3. Если все варианты уменьшить (увеличить) на постоянное число А, то средняя арифметическая из них уменьшится (увеличится) на это же число:
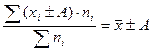 (4.14)
(4.14)
4. Если все варианты увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз:

(4.14)
5. Если все веса средней одинаково увеличить (уменьшить) в несколько раз, то средняя арифметическая не изменится.
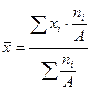 (4.15)
(4.15)
Дата добавления: 2015-02-25; просмотров: 1172;
