Средняя арифметическая простая
Является наиболее распространенным видом степенных средних, используется в случаях, когда объём усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности.
При этом если индивидуальные значения признака у статистических единиц заменить средней арифметической, то суммарный объем признака по совокупности в целом сохраняется неизменным. Это означает, что средняя арифметическая есть среднее слагаемое.
Средняя арифметическая простая используется при работе с несгруппированными данными и рассчитывается по формуле:
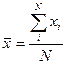 (4.11)
(4.11)
Например, известна сменная выработка рабочих бригады токарей:
| табельный номер рабочего | |||||
| количество изготовленных деталей, шт. |
Требуется определить среднюю выработку бригады.
Для ее нахождения используется формула средней арифметической простой:
Средняя арифметическая простая рассчитывается как:
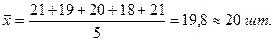
Средняя арифметическая взвешенная
Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным иливариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную– среднююсгруппированных величин.
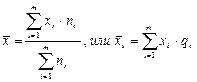 (4.12)
(4.12)
где 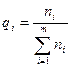 - частость, т. е. удельный вес статистических единиц, обладающих определенным значением признака в общем объеме совокупности.
- частость, т. е. удельный вес статистических единиц, обладающих определенным значением признака в общем объеме совокупности.
Пример: рассчитать среднюю продажную цену товара по данным, приведенным в таблице 4.1:
Таблица 4.1 - Объём продаж и цена товара А в магазинах города
| Магазины | Цена единицы товара, руб. | Объем продаж, шт. |
| Космос | ||
| Ариадна | ||
| Вега | ||
| Итого | ? |
Использовать среднюю арифметическую простую в данном случае нельзя, так как в разных магазинах продано разное количество товара А. Для расчёта средней продажной цены товара А. следует применить среднюю арифметическую взвешенную:
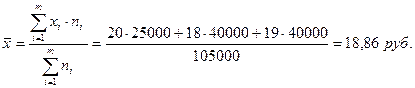
При применении средней арифметической простой средняя продажная цена товара составляла бы: х = (20 + 18 + 19) / 3 = 19 руб. , т.е. оказалась бы завышенной.
Дата добавления: 2015-02-25; просмотров: 1514;
