Свойства параллельного проецирования

1. Проекция точки есть точка. Это очевидно из определения проекции как точки пересечения проецирующего луча с плоскостью проекций.
2. Проекция прямой есть прямая (рис. 2). Для получения проекции прямой линии достаточно иметь проекции двух принадлежащих ей точек и через них провести прямую.

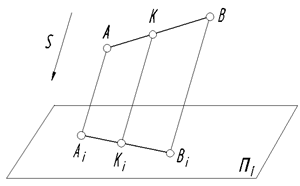
3. Проекция точки К, принадлежащей прямой АВ, находится на проекции этой прямой (рис. 5); К Î АВ; К_i Î А_i В_i

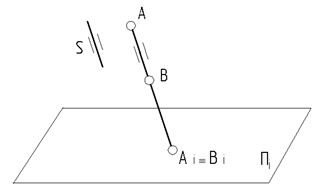
1. Проекций прямой, параллельной направлению проецирования, является точка (рис. 6).

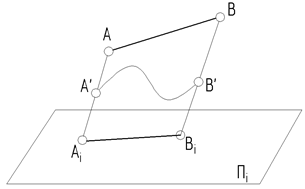
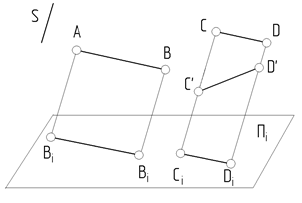
5. Прямая линия А_iВ_i может быть проекцией не только прямой АВ, но и любой кривой линии А¢В¢, если эта кривая линия находится в проецирующей плоскости (рис. 7).

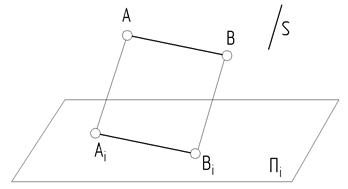
6. Если отрезок прямой АВ параллелен плоскости проекций, то его проекция на эту плоскость равна истинной величине отрезка (рис. 8).

AB ǁ П₁ Þ А_i В_i º AB

1. Отношение отрезков прямой линии равно отношению отрезков их проекций (рис. 5)

АК : КВ = А_i К_i : К_i В_i

8. Проекции параллельных прямых параллельны между собой. Но обратное справедливо не всегда (рис. 9)

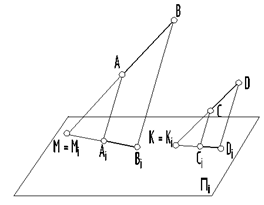AB ǁ CD; A_iB_i ǁ C_i D_i; AB ∦C¢D¢

9. Отношение отрезков параллельных прямых равно отношению проекций их отрезков (рис. 10). АВ ǁ CD, следовательно АВ/СD = A_iB_i/ C_iD_i что следует из подобия треугольников MBB_i и KDD_i.

Точка