Общие сведения. Из-за разнообразных неконтролируемых воздействий результаты измерения макроскопической величины имеют статистический характер
Из-за разнообразных неконтролируемых воздействий результаты измерения макроскопической величины имеют статистический характер. В основном это относится к статистичности процесса измерения. Возможны флуктуации и самой измеряемой величины, однако они могут быть сделаны сколь угодно малыми. Поэтому можно сказать, что сама по себе измеряемая величина (например, масса какого либо тела, длина стержня и т.д.) имеет некоторое вполне определённое значение, в то время как результаты измерений флуктуируют из-за несовершенства измерительных приборов, недостаточной их изоляции от изменяющихся внешних условий и т.д. Численные значения результатов измерений обычно распределены по некоторому непрерывному вероятностному закону, чаще всего по закону Гаусса.
Совсем иначе обстоит дело со многими измерениями в ядерной физике. В отличие от макромира в микромире флуктуации измеряемых величин связаны, как правило, с самой сутью явлений и поэтому не могут быть сделаны сколь угодно малыми.
Если, например, речь идёт об измерении числа актов радиоактивного распада, происшедшего за какое-то время, то флуктуирует сама измеряемая величина, а измерительный прибор (счётчик частиц) в первом приближении можно считать идеальным, т.е. не подверженным статистическому влиянию окружающих условий. Измеряемая величина (например, число актов радиоактивного распада) является уже не непрерывной, а дискретной, и наиболее характерным законом распределения, вместо закона Гаусса, является закон Пуассона, а иногда биномиальный закон.
Роль статистического подхода в микромире значительно глубже, чем в макрофизике. Статистика здесь нужна не только для обработки результатов измерений, но и для изучения самой природы исследуемых явлений. Например, природа радиоактивности была окончательно установлена только после завершения подробного статистического анализа, показавшего, что различные акты распада между собой статистически независимы. Другой пример. При исследовании космических лучей при помощи камеры Вильсона было обнаружено, что число частиц, регистрируемых при различных последовательных расширениях камеры, распределено не по закону Пуассона. Это наблюдение послужило отправной точкой для открытия и исследования ливней космических частиц.
Ошибки, связанные с методикой измерения, называют систематическими. Например, детекторы ядерных излучений и пересчётные устройства имеют конечное «мёртвое» время 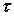 . Если в течение этого времени возникает несколько импульсов, то регистрирующее устройство не сможет сосчитать их раздельно, и, следовательно, просчитает часть импульсов. Просчёты, хотя и объясняются статистическим характером явлений, но приводят к систематической ошибке, зависящей от скорости счета и параметров системы, предназначенной для регистрации импульсов.
. Если в течение этого времени возникает несколько импульсов, то регистрирующее устройство не сможет сосчитать их раздельно, и, следовательно, просчитает часть импульсов. Просчёты, хотя и объясняются статистическим характером явлений, но приводят к систематической ошибке, зависящей от скорости счета и параметров системы, предназначенной для регистрации импульсов.
Пусть счётчик облучается потоком независимо следующих друг за другом частиц. Попадание той или иной частицы в счётчик является случайным событием. Поэтому в течение равных интервалов времени через счётчик может пролететь разное количество частиц. В этих условиях вероятность 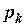 того, что в течение времени
того, что в течение времени 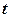 в счётчик попадёт
в счётчик попадёт 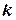 частиц, даётся известной формулой Пуассона:
частиц, даётся известной формулой Пуассона:
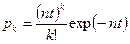 , (1)
, (1)
где 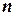 - поток частиц.
- поток частиц.
Среднее число актов определяется равенством
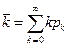 . (2)
. (2)
Если интенсивность не зависит от времени, то 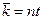 , откуда следует, что интенсивность
, откуда следует, что интенсивность 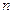 имеет смысл среднего числа актов, осуществляющихся за единицу времени.
имеет смысл среднего числа актов, осуществляющихся за единицу времени.
Тогда формулу (1) можно записать в виде
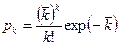 . (3)
. (3)
Как видно из (3), распределение Пуассона полностью определяется заданием только одного параметра – среднего числа актов. Экспериментальное определение 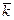 является, как правило, основной целью большей части измерений, проводимых в ядерной физике.
является, как правило, основной целью большей части измерений, проводимых в ядерной физике.
Из формулы (3) следует, что
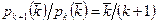 . (4)
. (4)
Поэтому, если 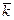 <<1, то
<<1, то 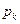 монотонно убывает с ростом
монотонно убывает с ростом 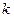 . иная картина имеет место, когда
. иная картина имеет место, когда 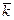 >1. В этом случае
>1. В этом случае 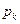 сначала возрастает, достигая максимального значения при
сначала возрастает, достигая максимального значения при 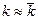 , после чего начинает монотонно убывать.
, после чего начинает монотонно убывать.
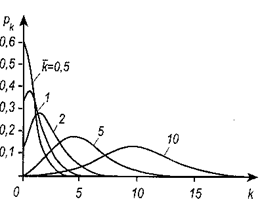
Рис. 1. Зависимость 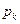 от
от 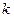 .
.
Зависимость 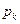 от
от 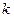 при разных значениях
при разных значениях 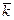 изображена на рис. 1. При малых значениях
изображена на рис. 1. При малых значениях 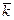 наблюдается асимметрия. По мере роста
наблюдается асимметрия. По мере роста 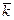 максимум становится относительно всё более острым, а график – всё более симметричным относительно
максимум становится относительно всё более острым, а график – всё более симметричным относительно 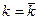 . При большом значении
. При большом значении 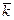 график практически симметричен.
график практически симметричен.
Из формулы (3) следует, что при всяком значении 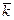 возможно осуществление любого числа актов
возможно осуществление любого числа актов 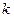 . Однако, не все события встречаются одинаково часто. Если величина
. Однако, не все события встречаются одинаково часто. Если величина 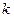 близка к
близка к 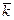 , то вероятность
, то вероятность 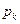 велика, в противном случае – мала. Мерой отклонения случайной величины
велика, в противном случае – мала. Мерой отклонения случайной величины 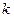 от её среднего значения (мерой флуктуации) является дисперсия.
от её среднего значения (мерой флуктуации) является дисперсия.
Дисперсией некоторой случайной величины 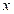 называется выражение:
называется выражение:
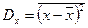 . (5)
. (5)
Величину 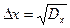 называют абсолютной флуктуацией случайной величины
называют абсолютной флуктуацией случайной величины 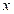 , а величину
, а величину 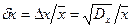 – её относительной флуктуацией.
– её относительной флуктуацией.
В случае закона Пуассона дисперсия
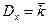 , (6)
, (6)
абсолютная флуктуация
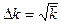 , (7)
, (7)
относительная флуктуация
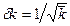 , (8)
, (8)
где 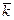 – среднее число актов.
– среднее число актов.
Соотношения (6)-(8) играют основную роль во всех приложениях закона Пуассона. Их смысл состоит в следующем. Если регистрировать отсчёты счётчика в очень большом числе равных интервалов, то в большей части интервалов число отсчётов 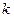 будет отличаться от
будет отличаться от 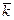 . не более чем на
. не более чем на 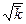 .
.
Абсолютная флуктуация (7) возрастает с ростом 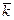 , однако относительная ошибка
, однако относительная ошибка 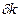 (8) уменьшается обратно пропорционально квадратному корню из числа сосчитанных частиц. Отсюда можно найти число частиц
(8) уменьшается обратно пропорционально квадратному корню из числа сосчитанных частиц. Отсюда можно найти число частиц 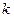 , которое нужно сосчитать для достижения заданной относительной ошибки
, которое нужно сосчитать для достижения заданной относительной ошибки 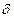 :
:
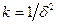 . (9)
. (9)
Таким образом, для измерения среднего числа частиц со статистической ошибкой 10%, нужно сосчитать 102 частиц. Для того чтобы статистическая ошибка составляла 1%, требуется уже 104 частиц и т.д.
Закон Пуассона определён только для положительных значений 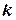 . На практике он часто применяется в тех случаях, когда нужно оценить надёжность измерений и ошибки измеренных величин в случае наблюдения редких событий (отличающихся малой интенсивностью).
. На практике он часто применяется в тех случаях, когда нужно оценить надёжность измерений и ошибки измеренных величин в случае наблюдения редких событий (отличающихся малой интенсивностью).
СВЯЗЬ РАСПРЕДЕЛЕНИЯ ПУАССОНА С РАСПРЕДЕЛЕНИЕМ ГАУССА
Выше уже отмечалось, что по мере роста 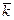 распределение Пуассона становится всё более симметричным относительно
распределение Пуассона становится всё более симметричным относительно 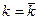 .
.
Если выполнено условие
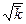 >>1 (10)
>>1 (10)
(практически при 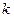 ≈20), то достигается полная симметрия. Кроме того, различие между величинами вероятностей для смежных или близких
≈20), то достигается полная симметрия. Кроме того, различие между величинами вероятностей для смежных или близких 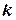 оказывается очень малым. Например, легко проверить, что при
оказывается очень малым. Например, легко проверить, что при 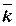 =1000:
=1000:
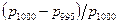 =0,01. (11)
=0,01. (11)
В этих условиях вместо вероятности 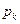 осуществления того или иного числа отсчётов можно пользоваться уже другой величиной, а именно, вероятностью
осуществления того или иного числа отсчётов можно пользоваться уже другой величиной, а именно, вероятностью 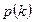 того, что число отсчётов заключено в «бесконечно малом» интервале от
того, что число отсчётов заключено в «бесконечно малом» интервале от 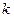 до
до 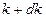 . По абсолютной величине интервал
. По абсолютной величине интервал 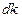 может содержать несколько единиц. Однако он мал по сравнению с интересующими нас
может содержать несколько единиц. Однако он мал по сравнению с интересующими нас 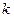 , равными по порядку величины среднему числу отсчётов
, равными по порядку величины среднему числу отсчётов 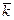 . Тем самым дискретное распределение заменяется непрерывным. Количественное рассмотрение функции распределения при выполнении условия (10) приводит к выводу, что рассматриваемая величина
. Тем самым дискретное распределение заменяется непрерывным. Количественное рассмотрение функции распределения при выполнении условия (10) приводит к выводу, что рассматриваемая величина 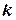 распределена по закону Гаусса:
распределена по закону Гаусса:
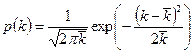 (12)
(12)
Закон Гаусса определён как для положительных, так и для отрицательных значений 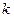 . Величина
. Величина 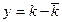 , имеющая смысл отклонения числа отсчётов
, имеющая смысл отклонения числа отсчётов 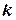 от среднего значения, распределена по закону
от среднего значения, распределена по закону
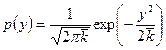 . (13)
. (13)
При помощи (13) можно вычислить вероятность того, что величина 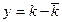 заключена в интервале от
заключена в интервале от 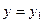 до
до 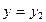 . Искомая вероятность
. Искомая вероятность
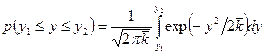 (14)
(14)
Заменяя переменную по формуле 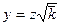 , получим
, получим
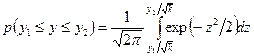 (15)
(15)
или 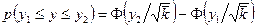 , (16)
, (16)
где 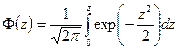 (1.17) – функция Гаусса.
(1.17) – функция Гаусса.
Значения функции Гаусса приводятся в разнообразных математических и физических справочниках. С помощью таблиц можно найти вероятность того, что отклонение от среднего не превосходит по модулю величины абсолютной ошибки 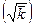 :
:
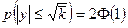 =0,682, (18)
=0,682, (18)
точно также получаем
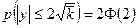 =0,954, (19)
=0,954, (19)
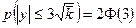 =0,997. (20)
=0,997. (20)
Из формул (18)-(20) вытекает следующее: если регистрировать отсчёты счётчика в большом числе равных интервалов времени, то при выполнении условия (10) в 68,2% случаев число отсчётов будет отличаться от 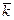 не более чем на
не более чем на 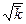 , в 95,4% не более чем на
, в 95,4% не более чем на 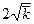 и в 99,7% не более чем на
и в 99,7% не более чем на 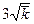 и т.д.
и т.д.
Результат измерения числа отсчётов 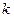 приводятся всегда вместе со своей абсолютной ошибкой (обычно
приводятся всегда вместе со своей абсолютной ошибкой (обычно 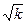 ), которая является показателем статистической точности измерений.
), которая является показателем статистической точности измерений.
Распределение (12)является частным случаем распределения Гаусса
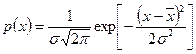 , (21)
, (21)
которое зависит от двух параметров – 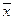 и
и 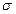 .
.
Часто используется представление распределения (21) в функции переменной 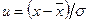 , тогда
, тогда
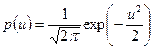 .
.
В таком представлении распределения Гаусса его среднее значение равно нулю, а стандартное отклонение – единице.
Распределение Гаусса является хорошим приближением для описания широкого круга статистических явлений. В ядерной физике распределение (21) описывает, например, распределение углов упругого рассеяния при прохождении заряженной частицы через вещество, распределение пробегов тяжёлых заряженных частиц в веществе, распределение импульсов по амплитудам при регистрации заряженных частиц полупроводниковым и сцинтилляционным детекторами и т.д.
Распределение Гаусса широко используется при анализе погрешностей эксперимента. Широкое применение нормального распределения в теории измерений основано на доказываемом в теории вероятности утверждения о том, что случайная величина, являющаяся суммой очень большого числа независимых случайных величин с практически произвольным распределением, распределена согласно (21). Последнее утверждение означает, что использование нормального закона при описании экспериментальных данных возможно в тех случаях, когда исследуемую случайную величину можно представить в виде суммы достаточно большого числа независимых элементарных слагаемых, каждое из которых сравнительно мало влияет на сумму. Такая ситуация часто характерна для сложных экспериментов. В качестве примера можно привести случай, когда случайная величина подчиняется равномерному (равновероятному) распределению: случайная величина, являющаяся суммой трёх таких величин уже может быть хорошо аппроксимирована распределением Гаусса.
РАСПРЕДЕЛЕНИЕ 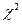 .
.
Распределение 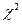 (хи-квадрат) находит широкое применение при проверке согласия экспериментальных данных с некоторой априорной гипотезой, получении доверительных интервалов для статистических параметров, проверке независимых переменных и в ряде других задач.
(хи-квадрат) находит широкое применение при проверке согласия экспериментальных данных с некоторой априорной гипотезой, получении доверительных интервалов для статистических параметров, проверке независимых переменных и в ряде других задач.
Пусть 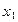 ,
, 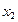 , …,
, …, 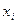 , …,
, …, 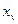 – набор
– набор 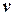 случайных величин, каждая из которых распределена по нормальному закону со своим математическим ожиданием
случайных величин, каждая из которых распределена по нормальному закону со своим математическим ожиданием 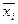 и дисперсией
и дисперсией 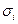 . Квадраты нормированных значений
. Квадраты нормированных значений 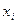
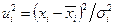 в силу случайности
в силу случайности 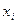 –также случайные величины. Их сумма также является случайной величиной
–также случайные величины. Их сумма также является случайной величиной
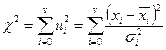 . (23)
. (23)
Очевидно, что величина 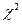 всегда положительна. Параметр
всегда положительна. Параметр 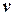 в (23) называют числом степеней свободы. Поскольку величины
в (23) называют числом степеней свободы. Поскольку величины 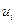 нормированы и имеют одно и тоже среднее значение, равное нулю, и равную единице дисперсию, то распределение плотности вероятности случайной величины
нормированы и имеют одно и тоже среднее значение, равное нулю, и равную единице дисперсию, то распределение плотности вероятности случайной величины 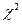 должно зависеть только от одного параметра, а именно от параметра
должно зависеть только от одного параметра, а именно от параметра 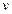 . Если не все
. Если не все 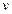 случайных величин независимы, то число степеней свободы, являющиеся параметром в распределении
случайных величин независимы, то число степеней свободы, являющиеся параметром в распределении 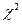 , меньше
, меньше 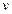 на число связей. Плотность распределения вероятности для
на число связей. Плотность распределения вероятности для 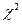 даётся формулой
даётся формулой
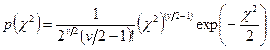 ,
, 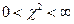 (24)
(24)
Среднее значение 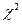 равно числу степеней свободы
равно числу степеней свободы 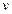 , а дисперсия
, а дисперсия 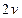 . Для приложений важно распределение накопленной вероятности
. Для приложений важно распределение накопленной вероятности
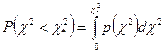 , (25)
, (25)
которое трудно получить непосредственным интегрированием. В руководствах и книгах по статистике приводятся подробные таблицы 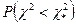 для различных
для различных 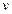 .
.
ПРОВЕРКА ГИПОТЕЗ О ЗАКОНЕ РАСПРЕДЕЛЕНИЯ. КРИТЕРИЙ СОГЛАСИЯ 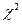 .
.
Целью многих экспериментов является оценка закона распределения некоторой физической величины. В ядерной физике это может быть, например, закон углового распределения нейтронов, рассеянных на ядрах определённого элемента. Точный закон распределения случайной величины в эксперименте определить невозможно, поскольку для этого понадобилось бы бесконечное число измерений для получения генеральной совокупности, а из конечного числа измерений определяется лишь конечная выборка. Из этого сразу следует важный вывод о том, что эксперимент не доказывает правильность гипотезы, а лишь позволяет сделать заключение о непротиворечивости её с данными эксперимента.
Обычно перед проведением опыта уже сформулирована одна или несколько априорных гипотез, полученных из теории или в результате предыдущих экспериментов, часто косвенных. Поскольку измеряемая величина случайная, то, даже если её закон распределения точно известен, ввиду ограниченности выборки будут наблюдаться отклонения результатов наблюдения от вычисленных по распределению. Возникает вопрос: случайны ли наблюдаемые отклонения измеренных величин от предсказанных теорией или имеются систематические расхождения, т.е. теория неверна?
Критерием согласия называют критерий проверки гипотезы о предполагаемом распределении. С его помощью можно установить, задавшись так называемой доверительной вероятностью, согласуются экспериментальные данные с априорной гипотезой или нет. Доверительная вероятность определяется условиями задачи и обычно принимается близкой к единице, например, 0,95.
На практике наиболее часто используется критерий согласия 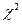 . Рассмотрим этот критерий. Пусть требуется проверить гипотезу о том, что случайная величина
. Рассмотрим этот критерий. Пусть требуется проверить гипотезу о том, что случайная величина 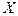 распределена по закону
распределена по закону 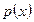 . Рассмотрим опыт, в котором получено
. Рассмотрим опыт, в котором получено 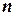 независимых измерений
независимых измерений 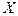 . Разобьём всю область измерений
. Разобьём всю область измерений 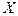 на
на 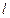 интервалов и подсчитаем количество
интервалов и подсчитаем количество 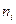 измеренных значений
измеренных значений 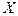 , попавших в каждый из интервалов. Поскольку теоретическое распределение
, попавших в каждый из интервалов. Поскольку теоретическое распределение 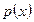 предполагается известным, можно рассчитать теоретическое число значений
предполагается известным, можно рассчитать теоретическое число значений 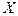 в
в 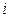 -том интервале
-том интервале 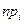 , где
, где 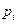 – вероятность попадания случайной величины в
– вероятность попадания случайной величины в 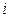 -тый интервал. Если экспериментальные частоты
-тый интервал. Если экспериментальные частоты 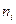 сильно отличаются от теоретических
сильно отличаются от теоретических 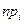 , то гипотезу о согласии теории и эксперимента следует отвергнуть. Критерий
, то гипотезу о согласии теории и эксперимента следует отвергнуть. Критерий 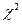 даёт возможность количественно выразить эту степень согласия.
даёт возможность количественно выразить эту степень согласия.
В качестве меры расхождения между теорией ( 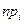 ) и экспериментом (
) и экспериментом ( 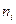 ) используют критерий:
) используют критерий:
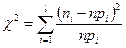 . (26)
. (26)
Ясно, что чем меньше различаются теоретические и экспериментальные частоты, тем меньше значение 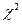 . поскольку распределение (26) при
. поскольку распределение (26) при 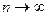 стремиться к распределению
стремиться к распределению 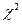 (см. формулу (24)), этот критерий, и назван критерием согласия
(см. формулу (24)), этот критерий, и назван критерием согласия 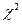 . Применяют его следующим образом: рассчитав значение
. Применяют его следующим образом: рассчитав значение 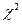 и задавшись доверительной вероятностью
и задавшись доверительной вероятностью 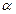 (или уровнем статистической значимости
(или уровнем статистической значимости 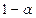 ) находят по таблицам значения
) находят по таблицам значения 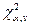 для
для 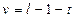 , где
, где 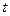 – количество дополнительных соотношений для оценки параметров распределения
– количество дополнительных соотношений для оценки параметров распределения 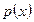 . Если при данном
. Если при данном 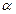
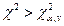 , то теория и эксперимент расходятся, если
, то теория и эксперимент расходятся, если 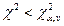 – согласуются. Также из таблиц можно определить доверительную вероятность
– согласуются. Также из таблиц можно определить доверительную вероятность 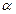 , при которой
, при которой 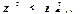 .
.
Рассмотрим пример. Проведено 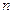 =200 измерений случайной величины. В таблице 1 приведены значения
=200 измерений случайной величины. В таблице 1 приведены значения 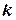 и частоты их появления
и частоты их появления 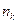 .
.
Таблица 1. Экспериментальные 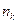 и ожидаемые по Пуассону
и ожидаемые по Пуассону 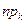 частоты.
частоты.
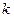
| Всего | |||||||
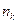
| ||||||||
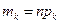
| 108,7 | 66,3 | 20,2 | 4,1 | 0,6 | 0,07 | 0,01 |
Необходимо проверить гипотезу о том, что эти данные подчиняются закону Пуассона, т.е. что
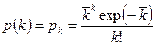 .
.
Мы видим, что для полного определения 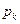 нужно оценить параметр
нужно оценить параметр 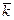 . Пусть этой оценкой будет выборочное среднее. Среднее
. Пусть этой оценкой будет выборочное среднее. Среднее 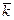 вычислим по формуле
вычислим по формуле
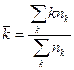 . (27)
. (27)
Таким образом,
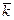 =(0×109+1×165+2×22+3×3+4×1)/200=122/200=0,61.
=(0×109+1×165+2×22+3×3+4×1)/200=122/200=0,61.
Тогда для ожидаемых частот получаем выражение
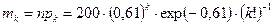 .
.
Эти значения приведены в третьей строке табл. 1. Поскольку ожидаемые частоты для 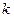 >2 малы, объединим последние четыре значения
>2 малы, объединим последние четыре значения 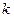 и составим новую таблицу 2.
и составим новую таблицу 2.
Таблица 2.
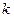
| 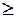 3 3
| |||
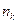
| ||||
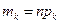
| 108,7 | 66,3 | 20,2 | 4,8 |
Для проверки гипотезы вычислим
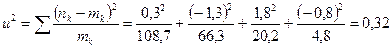
Для оценки 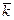 мы использовали одно соотношение (27), поэтому число степеней свободы равно
мы использовали одно соотношение (27), поэтому число степеней свободы равно 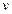 =4-1-1=2. Следовательно, величина
=4-1-1=2. Следовательно, величина 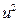 должна быть распределена примерно как
должна быть распределена примерно как 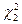 .
.
Выясним теперь, какова вероятность того, что указанное распределение случайной величины соответствует гипотезе о применимости закона Пуассона. С помощью таблицы 3, в верхней строке которой приведены значения доверительной вероятности 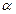 , находим, что полученное значение
, находим, что полученное значение 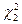 соответствует доверительной вероятности
соответствует доверительной вероятности 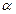 =0,80–0,90 (при необходимости результат можно уточнить интерполяцией). Таким образом, получена оценка вероятности
=0,80–0,90 (при необходимости результат можно уточнить интерполяцией). Таким образом, получена оценка вероятности 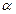 принять гипотезу и, соответственно, оценка
принять гипотезу и, соответственно, оценка 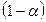 отвергнуть гипотезу.
отвергнуть гипотезу.
Дата добавления: 2015-02-25; просмотров: 864;
