Общие сведения. В настоящее время известно в природе много процессов, происходящих самопроизвольно, спонтанно

В настоящее время известно в природе много процессов, происходящих самопроизвольно, спонтанно. К числу таких процессов относится радиоактивный распад ядер. При радиоактивном распаде ядром атома могут испускаться альфа-частицы, бета-частицы (электроны, имеющие непрерывное распределение по энергии), нейтроны, протоны, гамма-лучи. Самопроизвольный распад радиоактивных ядер происходит по закону радиоактивного распада, согласно которому число ядер dN(t), распадающихся за бесконечно малый промежуток времени dt, пропорционально числу ядер N(t), имеющихся налицо в момент времени t:

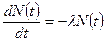. (1)

Коэффициент пропорциональности l называется постоянной распада ядра. Радиоактивная постоянная показывает долю ядер, распадающихся в единицу времени, другими словами, l – это вероятность распада. Знак минус в уравнении (1) соответствует убыванию количества ядер в процессе распада.

Если первоначально при t=0 имелось N₀ ядер то, используя закон радиоактивного распада, можно найти число оставшихся ядер по истечении времени t. Для этого необходимо проинтегрировать уравнение (1):

.

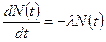Отсюда

.

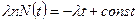Проинтегрировав это выражения и используя условие, что при t=0 N(0)=N₀, получим

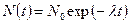. (2)

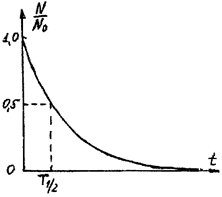
Рис.1. Кривая изменения числа ядер по времени.

Таким образом, число ядер радиоактивного распада уменьшается со временем по экспоненциальному закону. На рис. 1 представлена кривая изменения числа ядер во времени, происходящего по закону радиоактивного распада. Этот закон может быть применён только к большому числу радиоактивных ядер. При небольшом числе распадающихся ядер наблюдаются статистические колебания около среднего значения.

Радиоактивный распад – явление случайное, и «время жизни» каждого отдельного ядра не может быть определено заранее. Пользуясь постоянной распада 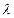, представляющей вероятность того, что ядро испытывает превращение в течение единицы времени, можно вычислить среднюю продолжительность жизни большого числа ядер.

Если 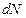– число ядер, распавшихся за промежуток времени между 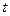и 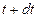, то ядра просуществовали время, равное 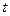, а общая продолжительность их жизни составит

.

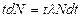Сумма продолжительности жизни всех 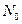атомов, существовавших в момент времени 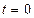, будет равна

.

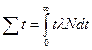Подставляя вместо 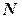его значение из формулы (2), получим

.

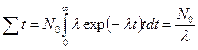Отсюда средняя продолжительность жизни ядра

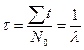. (3)

Практически для характеристики устойчивости данного радиоактивного изотопа обычно пользуются периодом полураспада. Период полураспада определяется промежутком времени, в течение которого распадается половина наличного количества ядер. Связь между периодом полураспада и радиоактивной постоянной 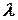легко выводится из формулы (2)

.

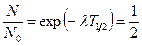Отсюда

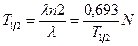. (4)

С учетом формулы (4) уравнение (1) может быть переписано в форме, удобной для экспериментального определения периода полураспада T_1/2 долгоживущих радиоактивных ядер (~10³-10⁹ лет).

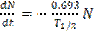(5)

Ряд естественных радиоактивных изотопов, в том числе и , имеют такие большие периоды полураспада, что для этих элементов количество ядер можно считать неизменным в течение столетий. Вследствие этого число ядер, распадающихся в единицу времени в единице веса, будет постоянно. Следовательно, используя формулу (5), можно определить период полураспада долгоживущего изотопа

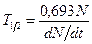. (6)

Радиоактивные атомы ⁴⁰К содержатся в естественной смеси изотопа калия в количестве 0,011% от общего числа атомов калия. Радиоактивный распад ядра атома 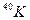в 89% случаев совершается путём испускания 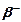– частиц с максимальной энергией 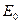=1,4 МэВ с образованием ядра 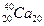(см. рис. 2) и в 11% случаев электронным захватом (е-захват) распадается на возбуждённое состояние 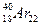, которое испускает g-квант с энергией 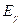=1,55 МэВ и переходит в основное состояние .

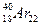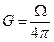. (7)

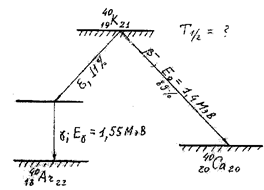
Рис. 2. Схема распада ⁴⁰K.

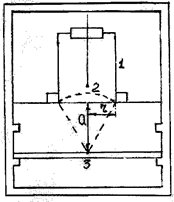
Рис. 3. 1) Счетчик Гейгера-Мюллера. 2) «Окно» счетчика. 3) Источник излучения.

Таким образом, регистрируя – частицы распада с помощью торцевого счётчика Гейгера-Мюллера; можно определить число ядер 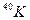, распадающихся в единицу времени. Однако, для определения числа частиц, испускаемых источником, необходимо учитывать следующие поправки:

1. Геометрический фактор. Если поместить точечный источник, испускающий частицы на определённом расстоянии от окошка счётчика (см. рис. 3), то достигнут окошка счётчика только те частицы, которые попадают в телесный угол 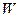. Излучение же от радиоактивного препарата распространяется в телесном угле 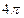. Геометрическим коэффициентом 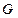называется отношение числа частиц, попавших в телесный угол 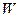, к общему числу частиц, испускаемых источником (телесный угол 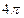). Телесный угол может быть заменён линейным углом 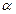и выражен через расстояние 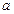и радиус окошка счётчика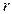

.

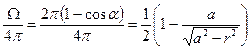Если имеется неточечный источник излучения, а радиоактивный препарат определённых размеров, то вычисление геометрического коэффициента, значительно усложняется. Для плоского препарата можно вычислить для данного счётного устройства по формуле Блахмана:

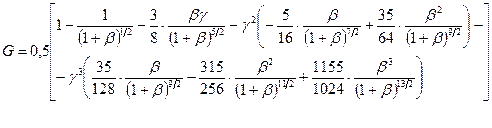, (8)

где 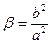, , 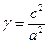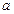- расстояние препарата от счётчика, 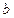-диаметр препарата.

Для нашей установки 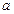=9 мм, 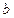=26 мм, 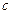=26 мм.

2. Эффективность счётчика к 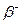-частицам. Для энергии 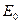=1,1 МэВ она близка к единице, то есть все 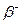-частицы, попавшие в счётчик, зарегистрируются. Таким образом, 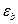=1.

3. Поправка на поглощение 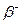-излучения окошком счётчика, слоем воздуха между 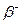-препаратом и окошком счётчика и лавсановой плёнкой, покрывающей источник.

Поглощение 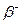- излучения веществом происходит по закону:

,

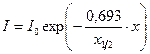где 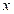- толщина поглотителя, 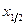– слой половинного ослабления.

Для частиц с энергией 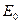=1,4 МэВ значение 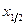=87 мг/см². Поверхностная плотность окошка счётчика и слоя воздуха в нашей установке составляет 3 мг/см². Поверхностная плотность лавсановой плёнки ≈3,6 мг/см².

Тогда поправка на поглощение

.

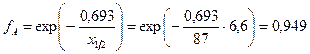4. Поправка на самопоглощение 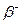-излучения. Может быть определена по формуле

.

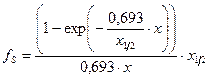Поверхностная плотность источника равна в нашем случае 58 мг/см². Тогда находим, что 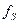=0,8.

5. Поправка на обратное рассеяние зависит от толщины подложки, на которой находится радиоактивное вещество. В нашем случае источник помещён на пластиковую подложку, поэтому следуют поправку на обратное рассеяние принять равной 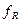=1.

6. Поправка на схему распада. Как видно из рис. 2, распад ⁴⁰К только в 89% случаев происходит с испусканием 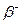-частиц, поэтому поправка на схему распада будет 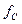=0,89.

Таким образом, измерив на установке скорость счёта 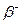-частиц 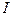(имп/мин) и вводя поправки, можно определить число 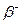-частиц, испущенных источником ⁴⁰К за 1 мин, а тем самым и количество распадающихся ядер (за 1 мин)

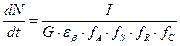. (11)

Для определения периода полураспада ⁴⁰К по формуле (3.6) необходимо знать также число ядер ⁴⁰К, содержащихся в источнике. Источником в данной работе служит химически чистая соль , нанесённая на алюминиевую подложку и покрытая тонкой лавсановой плёнкой. Содержание в молях в источнике излучения равно 3,75·10^-3. Зная число молекул в одном моле любого вещества ( 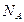=6,02·10²³ моль^-1) и содержание атомов ⁴⁰К в естественной смеси изотопов калия (0,011%), легко определить 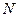– число ядер ⁴⁰Кв источнике ( 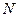=3,75·10^-3·6,02·10²³·0,011·0,01).

Далее при помощи формулы (6) можно определить период полураспада ⁴⁰К.

Регистрация 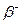-частиц в установке осуществляется торцевым счётчиком СБТ-13.