Общие сведения. Волновые свойства частиц

Волновые свойства частиц. Гипотеза де Бройля.

В 1924 г Луи де Бройль выдвинул гипотезу, согласно которой каждая материальная частица обладает волновыми свойствами, причем соотношения, связывающие волновые и корпускулярные характеристики частицы остаются такими же, как и в случае электромагнитного излучения. Напомним, что энергия E и импульс p фотона связаны с круговой частотой w и длиной волны l соотношениями

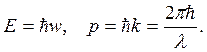
По гипотезе де Бройля движущейся частице, обладающей энергией E и импульсом p, соответствует волновой процесс, частота которого равна

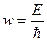, (1)

а длина волны

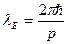. (2)

Как известно, плоская волна с частотой w, распространяющаяся вдоль оси x, может быть представлена в комплексной форме

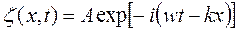
где A – амплитуда волны, а 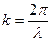– волновое число.

Согласно гипотезе де Бройля свободной частице с энергией E и импульсом p, движущейся вдоль оси x, соответствует плоская волна

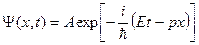(3)

распространяющаяся в том же направлении и описывающая волновые свойства частицы. Эту волну называют волной де Бройля. Соотношения, связывающие волновые и корпускулярные свойства частицы

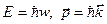, (4)

где 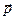– импульс частицы, а 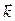– волновой вектор, получили название уравнений де Бройля.

Эффект Рамзауэра.

Ранее К. Рамзауэр, исследуя упругое рассеяние электронов на атомах аргона, обнаружил явление, которое не находило объяснения в рамках классической физики. Лишь через несколько лет стало ясно, что это явление представляет собой еще одно подтверждение волновых свойств электрона и является электронным аналогом хорошо известного в оптике пятна Пуассона.

Рамзауэр исследовал поперечное сечение упругого рассеяния электронов s на атомах аргона при энергии электронов E от долей электрон-вольта до нескольких десятков электрон-вольт. Сечение упругого рассеяния электронов определяется выражением

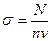, (5)

где N – число актов упругого рассеяния электронов на атомах аргона в единицу времени, n – плотность электронов в пучке, а v – их скорость. Сечение упругого рассеяния s имеет размерность площади, оно представляет собой площадь мишени вокруг атома, попадая в которую электрон испытывает упругое рассеяние.

Сечение упругого рассеяния зависит от энергии электронов E. Действительно, чем больше E, тем больше скорость электрона v и тем меньше угол, на который отклоняется электрон при взаимодействии с атомом при прочих равных условиях. Это означает, что при уменьшении энергии (скорости) электронов сечение упругого рассеяния должно увеличиваться.

Качественный вид результатов измерения Рамзауэра приведен на рис. 1. Для энергий электронов, превышающих 16 эВ, сечение рассеяния s возрастает с уменьшением E в соответствии с предсказаниями классической теории. Однако при дальнейшем уменьшении E картина качественно меняется. При энергии электронов меньше 16 эВ сечение рассеяния убывает с уменьшением E и при E» 1 эВ, s практически обращается в нуль. При дальнейшем уменьшении энергии электронов сечение рассеяния вновь возрастает.

Обращение s в нуль означает, что атомы аргона становятся как бы прозрачными для электронов, т.е. электрон проходит через атом аргона, не рассеиваясь на нем. Этот экспериментальный результат, совершенно не совместимый с представлениями классической физики, находит свое объяснение при учете волновой природы электрона.

В дальнейшем подобное явление было обнаружено и для атомов других инертных газов - криптона и ксенона. То обстоятельство, что эффект Рамзауэра наблюдается только в инертных газах, объясняется тем, что атомы инертных газов имеют полностью заполненную внешнюю электронную оболочку, они сферически симметричны и обладают достаточно резкой внешней границей.

Рис. 1. Качественная зависимость сечения упругого рассеяния электронов на атомах аргона от энергии электронов

Внутри атома потенциальная энергия налетающего электрона U отлична от нуля, скорость электрона меняется, становясь равной v в соответствии с законом сохранения энергии:

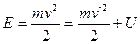, (6)

а значит, изменяется и длина его волны де Бройля. Таким образом, по отношению к электронной волне атом ведет себя как преломляющая среда с относительным показателем преломления

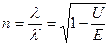. (7)

Решение задачи о рассеянии электрона на сферической потенциальной яме достаточно громоздко, поэтому рассмотрим простую модель: пусть электрон рассеивается на одномерной потенциальной яме конечной глубины. Решение задачи о прохождении частицы с энергией E над потенциальной ямой шириной l и глубиной U₀ (см. рис. 2) подробно рассмотрено в учебной литературе.

Уравнение Шредингера в данном случае имеет вид

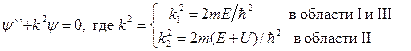(8)

Коэффициент прохождения равен отношению квадратов амплитуд прошедшей и падающей волн. В итоге получим

Рис. 2. Схематическое изображение прямоугольной ямы, над которой пролетает частица с энергией E.

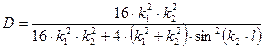(9)

или

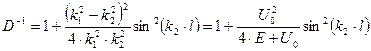. (10)

Видно, что коэффициент прохождения частицы над ямой имеет, в зависимости от ее энергии, ряд чередующихся максимумов. В частности, при k₂l=p коэффициент прохождения равен единице, т.е. отраженная волна, отсутствует, и электрон беспрепятственно проходит через атом, что является квантовым аналогом просветления оптики.

Таким образом, коэффициент прохождения электрона максимален при условии

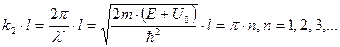(11)

откуда

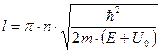. (11а)

Для объяснения эффекта Рамзауэра не обязательно прибегать к аппарату квантовой механики, достаточно использовать соотношение де Бройля и рассмотреть интерференцию волн де Бройля. Движущемуся электрону соответствует волна, длина которой определяется соотношением

,

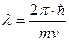где m – масса электрона, v – его скорость. Если кинетическая энергия электрона невелика, то

.

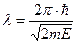При прохождении электрона через атом длина волны де Бройля становится меньше

,

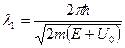где U₀ – увеличение энергии за счет взаимодействия электрона с атомом.

При этом происходит интерференция прошедших через атом волн 1 и 2, отраженных от передней и задней границ атома рис. 3. Пусть l – эффективный размер атома. Прошедшая волна 1 усилится волной 2, если разность хода между ними D = 2l = l₁ – условие 1-го интерференционного максимума, т.е. при условии:

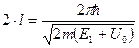
Прошедшая волна ослабится, если

,

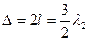условие интерференционного минимума, т.е.

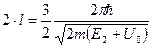
Решая эти два уравнения совместно, исключая U₀ определяем «эффективный» размер атома:

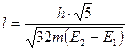. (11б)

Рис. 3. Схема рассеяния электрона на неподвижном атоме (а) и положения интерференционного максимума и минимума на вольтамперной характеристике тиратрона (б).

Описание установки.

В данной работе для изучения эффекта Рамзауэра используется тиратрон ТГ3-01/1.3, заполненный ксеноном. Схематическое изображение тиратрона приведено на рис. 4.

Электроны, эмитируемые катодом тиратрона, ускоряются напряжением U, приложенным между катодом и ближайшей к нему сеткой. Затем электроны рассеиваются на атомах инертного газа. Рассеянные электроны отклоняются в сторону и уходят на сетку, а оставшаяся часть электронов достигает анода и создает анодный ток I_a. Таким образом, поток электронов N(x) на расстоянии x от ускоряющей сетки (число электронов, проходящих через поперечное сечение лампы в точке x в единицу времени) уменьшается с ростом x от начального значения N₀ у катода (в точке x=0) до некоторого значения N_a у анода (в точке x=L).

Рассмотрим вольтамперную характеристику (ВАХ) тиратрона. Выделим в газе на расстоянии x от катода тонкий слой с площадью поперечного сечения S и толщиной dx (см. рис. 4). Этот слой содержит v=n_a× S×dx атомов газа (n_a – концентрация атомов газа в лампе). Суммарная рассеивающая поверхность этих атомов (эффективное суммарное сечение рассеяния) D=vD_a, где D_a – площадь поперечного сечения атома. Пусть dN есть убыль потока электронов в результате прохождения dx, тогда dN/N(x) – доля рассеянных электронов или вероятность рассеяния в слое. Для рассеяния электрона в слое необходимо выполнение двух независимых событий – электрон должен столкнуться с атомом в рассматриваемом слое и должен на этом атоме рассеяться. Следовательно, вероятность рассеяния электрона в слое равна произведению двух вероятностей – вероятности для электрона в слое dx встретиться

Рис. 4. Схематичное изображение тиратрона.

с атомом газа (она равна D/S – доли площади поперечного сечения слоя, перекрываемого атомами) и вероятности рассеяния на атоме w(V):

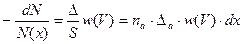(12)

Интегрируя это соотношение от 0 до L:

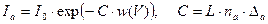, (13)

где I₀=e×N₀ – ток катода, I_a=e×N_а – анодный ток.

Согласно классическим представления, сечение рассеяния электрона на атоме должно падать монотонно с ростом V (обратно пропорционально скорости электрона), а значит, ВАХ будет монотонно возрастающей функцией, как это показано на рис. 5а.

Исходя из квантовомеханических представлений, вероятность рассеяния электронов и соответствующая ВАХ должны иметь вид, показанный на рис. 5б. Согласно формуле (13), по измеренной ВАХ тиратрона можно определить зависимость вероятности рассеяния электрона от его энергии из соотношения

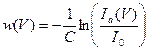. (14)

Реально удается надежно наблюдать лишь один (первый n=1) минимум в сечении рассеяния электронов. Дело в том, что уже при n=2 напряженность поля становится столь велика, что с большей вероятностью происходит ионизация атома и возникает пробой тиратрона. Поэтому измерения проводятся при пониженных величинах накала тиратрона. Кроме того, как показывает расчет, ростом n глубина минимума резко уменьшается.

Рис. 5. Качественный вид вероятности рассеяния электрона атомом инертного газа и ВАХ тиратрона в классическом (а) и квантовомеханическом представлениях (б).

Принципиальная схема экспериментальной установки изображена на рис. 6. Внешний вид передней панели прибора показан на рис. 7. Схема может работать в двух режимах: статическом и динамическом. Переключение режимов работы осуществляется тумблером T. В статическом режиме разность потенциалов между катодом и анодом постоянна, но регулируется потенциометром R₂ в интервале от 0 до 19 В. В динамическом режиме между катодом и анодом существует переменное напряжение частотой 50 Гц, амплитуду которого можно регулировать тем же потенциометром, что и в статическом режиме. Динамический режим используется для наблюдения на экране осциллографа зависимости тока коллектора от разности потенциалов между катодом и анодом. Статический режим необходим для снятия этой зависимости по точкам. В этом случае напряжение между катодом и анодом измеряется вольтметром V₂, а ток коллектора – микроамперметром mA. Напряжение накала подается от стабилизированного источника питания, которое измеряется вольтметром V₁ и регулируется потенциометром R₁ в интервале от 0 до 3 B.

Рис. 6. Схема экспериментальной установки.

Рис. 7. Передняя панель прибора.