Математическое выражение для кривой Лиссажу

,

где A, B – амплитуды колебаний, a, b – частоты, δ – сдвиг фаз.

Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности 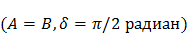и отрезка прямой 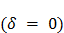. Ещё один пример фигуры Лиссажу – парабола .

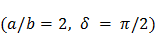При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии 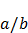– рациональное число.

Фигуры Лиссажу, где 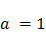, 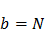( 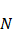– натуральное число) и

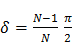(4)

являются полиномами Чебышева первого рода степени .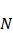

Фигуры Лиссажу можно наблюдать, например, на экране электронно-лучевого осциллографа, если к двум парам отклоняющих пластин подведены переменное напряжения с равными или кратными периодами. Вид фигур Лиссажу позволяет определить соотношения между периодами и фазами обоих колебаний. Если колебания, которые совершает точка, происходят не по гармоническому, а по более сложному закону, но с одинаковым периодом, то получаются замкнутые траектории, аналогичные фигурам Лиссажу но искажённой формы. По виду этих фигур можно судить о форме колебаний. Таким образом, наблюдение фигур Лиссажу – удобный метод исследования соотношений между периодами и фазами колебаний, а также и формы колебаний.