Теория лабораторной работы. Если образец из ферромагнитного вещества поместить во внешнее магнитное поле напряженностью , то внутри образца магнитная индукция будет равна:
Если образец из ферромагнитного вещества поместить во внешнее магнитное поле напряженностью 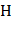 , то внутри образца магнитная индукция будет равна:
, то внутри образца магнитная индукция будет равна:
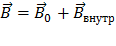 (5)
(5)
где: 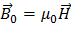 ,
, 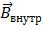 – индукция магнитного поля, создаваемая намагниченным веществом образца,
– индукция магнитного поля, создаваемая намагниченным веществом образца, 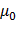 – магнитная постоянная, равная
– магнитная постоянная, равная 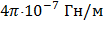 .
.
Для ферромагнитных веществ (ферромагнетиков) и малых намагничивающих полей 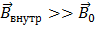 . Для малых
. Для малых 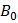 формулу (5) можно представить в виде:
формулу (5) можно представить в виде:
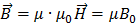 .
.
Пусть образец перед намагничиванием был полностью размагничен. Поместим его во внешнее поле, которое будем увеличивать от нуля до некоторого значения 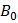 . Зависимость
. Зависимость 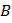 от
от 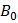 выразится кривой oa (см. рис.13). Если теперь уменьшать поле до нуля, то зависимость
выразится кривой oa (см. рис.13). Если теперь уменьшать поле до нуля, то зависимость 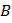 от
от 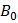 уже изобразится кривой ac.
уже изобразится кривой ac.
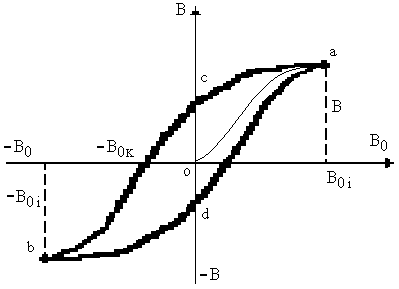 Рис. 13.
Рис. 13.
|
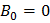 магнитная индукция образца отличается от нуля: в ферромагнетике наблюдается остаточное намагничивание, численно равное отрезку oc. Чтобы полностью размагнитить образец, следует создать магнитное поле напряженности
магнитная индукция образца отличается от нуля: в ферромагнетике наблюдается остаточное намагничивание, численно равное отрезку oc. Чтобы полностью размагнитить образец, следует создать магнитное поле напряженности 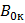 , направленное в противоположную сторону. Величина
, направленное в противоположную сторону. Величина 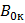 называется коэрцитивной (задерживающей) силой. Увеличивая поле
называется коэрцитивной (задерживающей) силой. Увеличивая поле 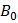 обратного направления до
обратного направления до 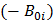 , получим часть cb кривой намагничивания. Снова уменьшая поле до нуля, получим часть bd. Поменяв направление поля на первоначальное и увеличивая его от нуля до
, получим часть cb кривой намагничивания. Снова уменьшая поле до нуля, получим часть bd. Поменяв направление поля на первоначальное и увеличивая его от нуля до 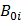 , вернемся в точку a по кривой da. Полученная кривая является петлей гистерезиса.
, вернемся в точку a по кривой da. Полученная кривая является петлей гистерезиса.
Ферромагнитные материалы применяются в трансформаторах, дросселях, машинах переменного тока, т. е. в устройствах, где они подвергаются периодическому перемагничиванию. Изучение магнитных характеристик ферромагнетиков в переменных полях представляет, поэтому, большой практический интерес. Основные характеристики ферромагнетиков – их коэрцитивная сила, магнитная проницаемость, мощность, рассеиваемая в виде тепла при перемагничивании и т. д. зависят от частоты перемагничивающегося поля. В настоящей работе кривые гистерезиса трансформаторной стали изучаются с помощью электронного осциллографа.
Значение площади петли гистерезиса данного образца пропорционально тепловой энергии, выделяющейся при перемагничивании. Можно дать качественную оценку определенному сорту трансформаторной стали, если сравнивать площади петель гистерезиса образцов.
Обмотка возбуждения трансформатора включается в сеть. Количество витков подобрано так, что в сердечнике наступает магнитное насыщение. На потенциометре 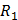 возникает соответственно переменная ЭДС, величина которой пропорциональна напряженности магнитного поля
возникает соответственно переменная ЭДС, величина которой пропорциональна напряженности магнитного поля 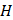 , намагничивающего сердечник. Эту ЭДС подают на горизонтально отклоняющие пластины X осциллографа (предварительно усилив усилителем горизонтального отклонения).
, намагничивающего сердечник. Эту ЭДС подают на горизонтально отклоняющие пластины X осциллографа (предварительно усилив усилителем горизонтального отклонения).
На вертикальные пластины осциллографа Y подается напряжение, возникающее на вторичной обмотке. Это напряжение, однако, пропорционально не магнитной индукции 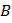 , а скорости изменения магнитной индукции
, а скорости изменения магнитной индукции 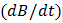 . Между вторичной обмоткой и осциллографом, поэтому, включается интегрирующее звено. Интегрирование напряжения проще всего осуществить при помощи
. Между вторичной обмоткой и осциллографом, поэтому, включается интегрирующее звено. Интегрирование напряжения проще всего осуществить при помощи 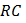 –ячейки, удовлетворяющей условию
–ячейки, удовлетворяющей условию 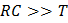 , где
, где 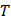 – период изучаемого явления. При большом сопротивлении
– период изучаемого явления. При большом сопротивлении 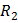 падение напряжения на конденсаторе мало по сравнению с падением напряжения на резисторе, так что ток через ячейку равен:
падение напряжения на конденсаторе мало по сравнению с падением напряжения на резисторе, так что ток через ячейку равен: 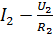 , где
, где 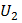 – напряжение на выходе вторичной обмотки. Напряжение на конденсаторе, которое подается на вход осциллографа, равно:
– напряжение на выходе вторичной обмотки. Напряжение на конденсаторе, которое подается на вход осциллографа, равно:
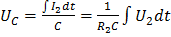 . (6)
. (6)
Из этого уравнения видно, что ячейка не только интегрирует напряжение, но и ослабляет его.
В данной схеме напряжение 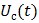 на конденсаторе
на конденсаторе 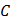 пропорционально не току
пропорционально не току 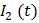 , а интегралу от тока. Подобное соединение конденсатора
, а интегралу от тока. Подобное соединение конденсатора 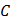 и резистора
и резистора 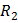 называется интегрирующей цепочкой.
называется интегрирующей цепочкой.
Таким образом, на экране осциллографа получается петля гистерезиса 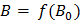 . За один период синусоидального изменения тока электронный луч опишет на экране полную петлю гистерезиса. На переменном токе промышленной частоты на экране будет видна неподвижная петля гистерезиса. Изменяя потенциометром
. За один период синусоидального изменения тока электронный луч опишет на экране полную петлю гистерезиса. На переменном токе промышленной частоты на экране будет видна неподвижная петля гистерезиса. Изменяя потенциометром 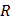 напряжение
напряжение 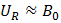 , на экране получаем ряд различных по площади петель, вершины которых находятся на кривой намагничивания. Для построения кривых намагничивания необходимо снять координаты вершин петель гистерезиса; (точки а и b). После этого следует определить величины
, на экране получаем ряд различных по площади петель, вершины которых находятся на кривой намагничивания. Для построения кривых намагничивания необходимо снять координаты вершин петель гистерезиса; (точки а и b). После этого следует определить величины 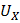 и
и 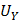 с учётом чувствительности пластин осциллографа
с учётом чувствительности пластин осциллографа 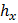 и
и 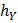 :
:
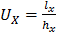 ;
; 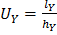 , (7)
, (7)
где 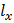 и
и 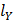 – координаты вершин петель гистерезиса.
– координаты вершин петель гистерезиса.
Вычислить значения: 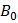 и
и 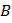 по формулам:
по формулам:
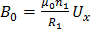 ,
, 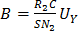 , (8)
, (8)
где 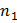 – число витков на единицу длины.
– число витков на единицу длины.
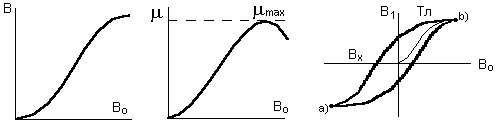 Рис. 14
Рис. 14
|
По вычисленным значениям
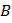 и
и 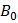 строится кривая намагничивания (рис.14).
строится кривая намагничивания (рис.14).
Дата добавления: 2015-02-23; просмотров: 839;
