Теория лабораторной работы. Для определения частоты неизвестного гармонического колебания часто используется метод фигур Лиссажу
Для определения частоты неизвестного гармонического колебания часто используется метод фигур Лиссажу, который заключается в следующем: исследуемое колебание складывается с взаимно-перпендикулярным ему колебанием известной частоты. В общем случае в результате сложения получаются фигуры Лиссажу, по общему виду которых можно определить частоты исследуемого напряжения. В настоящей работе сравнение частот производится с помощью электронного осциллографа, на вертикально отклоняющие пластины которого подается исследуемое напряжение от источника колебаний звуковой частоты, а на горизонтально отклоняющие пластины - напряжение определенной частоты от другого генератора.
Рассмотрим два взаимно-перпендикулярных колебания 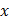 и
и 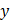 с частотами
с частотами 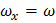 и
и 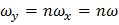 .
.
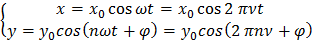 (5)
(5)
где 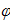 - начальная разность фаз между колебаниями. Очевидно,
- начальная разность фаз между колебаниями. Очевидно, 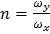
Система уравнений (5) представляет собой уравнение кривой, являющейся результатом сложения этих колебаний, заданной в параметрической форме. Определим уравнение траектории точки, участвующей в данных колебаниях, исключая из уравнения (5) время 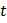 :
:
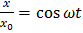 ;
; 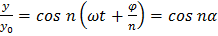 , где
, где 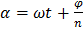 (6)
(6)
Прибавим к левой и правой части (6) минимальную величину 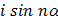 , получим:
, получим:
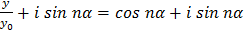 .
.
По формуле Муавра:  .
.
Продолжим преобразования:
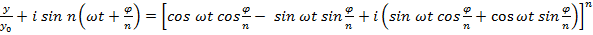 .(7)
.(7)
Но 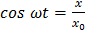 ;
; 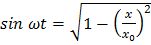 .
.
Подставляя эти значения в формулу (7), получим:
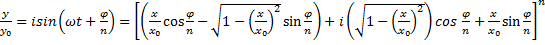 .(8)
.(8)
Разлагая по биному Ньютона выражение в квадратных скобках и приравнивая действительные части слева и справа, получим уравнение траектории колеблющейся точки.
Рассмотрим частный случай - сложение колебаний с одинаковыми частотами
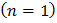 ,
, 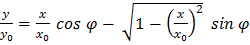 ,
,
Откуда: 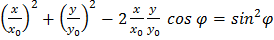 . (9)
. (9)
Это уравнение в общем случае является уравнением эллипса. Рассмотрим частные случаи этого уравнения. Пусть колебания происходят с разностью фаз равной нулю или 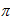 . В этом случае уравнение (9) принимает вид:
. В этом случае уравнение (9) принимает вид:
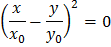
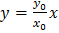 , или
, или 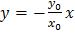 ,
,
т.е. эллипс вырождается в прямую (рис. 7).
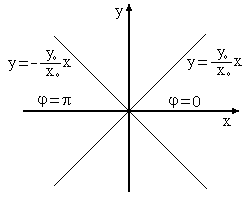 Рис. 7.
Рис. 7.
|
 . Тогда уравнение (9) будет иметь вид:
. Тогда уравнение (9) будет иметь вид: 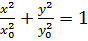 .
.
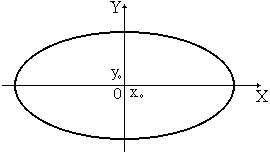 Рис. 8.
Рис. 8.
|
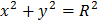 . В тех случаях, когда
. В тех случаях, когда 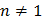 , по общему виду уравнения результирующего колебания, получаемого по формуле (8), трудно судить о форме траектории.
, по общему виду уравнения результирующего колебания, получаемого по формуле (8), трудно судить о форме траектории.
Пусть показатель степени в уравнении (8) есть число рациональное, т, е. может быть представлено в виде отношения двух целых чисел 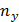 и
и 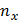 :
:
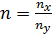 .
.
Из системы уравнений (5) следует, что:
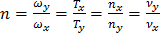 ,
,
где 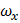 и
и 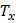 – частота и период колебаний в направлении оси
– частота и период колебаний в направлении оси 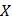 ;
; 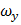 и
и 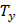 – частота и период колебаний в направлении оси
– частота и период колебаний в направлении оси 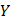 . Перепишем последнее соотношение в виде:
. Перепишем последнее соотношение в виде:
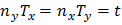 .
.
Отсюда следует, что за промежуток времени 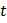 точка совершит
точка совершит 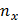 полных колебаний в направлении оси
полных колебаний в направлении оси 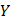 и
и 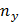 полных колебаний в направлении оси
полных колебаний в направлении оси 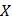 .
.
После истечения времени 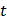 точка будет находиться в той же фазе, что и в начальный момент, т. е. за следующий промежуток времени
точка будет находиться в той же фазе, что и в начальный момент, т. е. за следующий промежуток времени 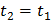 колебания в точности повторятся. В результате колебания будут накладываться сами на себя и дадут устойчивую картину (фигуры Лиссажу). Если же одно из чисел
колебания в точности повторятся. В результате колебания будут накладываться сами на себя и дадут устойчивую картину (фигуры Лиссажу). Если же одно из чисел 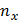 или
или 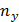 иррациональное, т. е.
иррациональное, т. е. 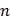 нельзя представить в виде отношения целых чисел, то это приведет к добавочной разности фаз. В результате картина результирующего колебания будет непрерывно изменяться. Если частота одного из колебаний известна, то по виду фигур Лиссажу можно определить частоту другого. Такое сравнение частот можно проделать осциллографическим методом, подавая на горизонтально отклоняющие пластины напряжение с известной частотой
нельзя представить в виде отношения целых чисел, то это приведет к добавочной разности фаз. В результате картина результирующего колебания будет непрерывно изменяться. Если частота одного из колебаний известна, то по виду фигур Лиссажу можно определить частоту другого. Такое сравнение частот можно проделать осциллографическим методом, подавая на горизонтально отклоняющие пластины напряжение с известной частотой 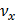 а на вертикально отклоняющие пластины – исследуемое напряжение с частотой
а на вертикально отклоняющие пластины – исследуемое напряжение с частотой 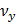 .
.
Пусть 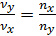 , тогда:
, тогда:  . (10)
. (10)
Выведем правило нахождения отношения частоты по фигурам Лиссажу. Учитывая уравнение (10), можно переписать уравнение (8) в виде:
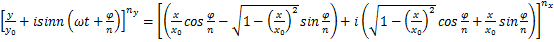 .
.
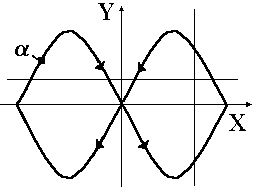 Рис. 9.
Рис. 9.
|
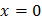 . Тогда, возводя левую и правую части по биному Ньютона и приравнивая действительные части, получим уравнение
. Тогда, возводя левую и правую части по биному Ньютона и приравнивая действительные части, получим уравнение 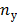 – степени относительно
– степени относительно 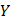 , имеющее
, имеющее 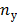 корней. Графически это означает, что ось
корней. Графически это означает, что ось 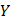 пересекает кривую
пересекает кривую 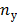 раз. Если
раз. Если 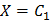 , где
, где 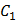 – произвольная постоянная, то получим так же уравнение, имеющее
– произвольная постоянная, то получим так же уравнение, имеющее 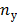 корней.
корней.
Фигура Лиссажу будет пересекать 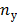 раз прямую, параллельную оси
раз прямую, параллельную оси 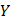 .
.
Полагая 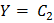 , получим уравнение
, получим уравнение 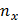 степени относительно X, т. е. кривая будет пересекать прямую, параллельную оси
степени относительно X, т. е. кривая будет пересекать прямую, параллельную оси 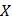 ,
, 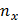 раз. Так на рис. 9
раз. Так на рис. 9 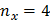 и
и 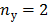 . Следовательно,
. Следовательно, 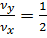
[1] Градуировка средств измерений (нем. graduiren — градуировать, лат. gradus — шаг, ступень, степень) — метрологическая операция, при помощи которой средство измерения (меру или измерительный прибор) снабжают шкалой или градуировочной таблицей (кривой).
[2] 1 эВ равен работе, совершаемой силами поля при перемещении элементарного электрического заряда (заряда, равного заряду электрона) при прохождении им разности потенциалов в 1 В. Так как заряд электрона равен 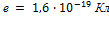 , то
, то 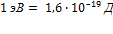 ж.
ж.
[3] Согласно квантово - механическому принципу Паули один энергетический уровень могут занимать не более двух электронов.
[4] Запрещённая зона (энергетическая щель) – область значений энергий в энергетическом спектре кристалла, которыми не могут обладать электроны, фононы или др. квазичастицы. Запрещенная зона отделяет одну разрешенную зону от другой.
[5] В общем случае магнитная проницаемость конкретного вещества зависит от многих факторов: напряженности магнитного поля, формы рассматриваемого поля (так как конечные размеры любого магнетика приводят к появлению встречного поля, уменьшающего первоначальное), температуры, частоты изменения магнитного поля, наличия дефектов структуры и т.д.
[6] Макротокаминазываются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел.
[7] Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах.
[8] Гистерезис (от греч. hysteresis — отставание, запаздывание), явление, которое состоит в том, что физическая величина, характеризующая состояние тела (например, намагниченность), неоднозначно зависит от физические величины, характеризующей внешние условия (например, магнитного поля).
[9] В общем случае магнитная проницаемость конкретного вещества зависит от многих факторов: напряженности магнитного поля, формы рассматриваемого поля (так как конечные размеры любого магнетика приводят к появлению встречного поля, уменьшающего первоначальное), температуры, частоты изменения магнитного поля, наличия дефектов структуры и т.д.
[10] Макротокаминазываются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел.
[11] Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах.
[12] Гистерезис (от греч. hysteresis — отставание, запаздывание), явление, которое состоит в том, что физическая величина, характеризующая состояние тела (например, намагниченность), неоднозначно зависит от физические величины, характеризующей внешние условия (например, магнитного поля).
[13] За одно полное колебание тело проходит расстояние S =4A.
Дата добавления: 2015-02-23; просмотров: 1389;
