Реологические свойства и модели жидкостей, встречающихся при бурении.

Реология – наука о течении сред. Реологические уравнения описывают связь касательного напряжения с деформированием среды, прежде всего скоростью сдвига слоев среды.

Широко распространены следующие реологические уравнения (модели) сред:

1. модель идеальной среды: t=0 (1)

2. модель реальных сред: предполагает, что при движении среды (жидкости) между ее слоями возникают касательные напряжения t не равно 0 (2).

В частности:

Модель вязкой среды (ньютоновской) среды (вода, воздух, керосин, бензин). В этой среде касательные напряжения связаны с градиентом скорости сдвига dU/dr формулой t=h(dU/dr) (3), где h - динамическая вязкость (Па*с). h=μ.

Вязкость h можно найти из простого опыта. Пластина 1 с помощью силы F движется по смоченной исследуемой жидкостью поверхности. Площадь соприкосновения S. Возникает касательное напряжение t= F/ S. При этом скорость распределяется по представленной треугольной эпюре. Рассмотрим два слоя, находящихся на расстоянии Δr друг от друга. Разность скоростей ΔU.

Lim(ΔU/ Δr)=dU/dr = размерность 1/с. h=t (dU/dr). Ньютон заметил, что отношение t (dU/dr)=const. Ctg α=t(dU/dr). t=(1/tgα)*(dU/dr). (1/tgα)=h.

Динамическая вязкость характеризует соседних слоев среды сопротивляться относительно сдвигу за счет влияния молекулярных сил.

Модель неньютоновских сред (буровые и тампонажные жидкости).

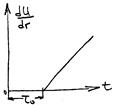
Бингамовские (ВПЖ) t=t₀₊h(dU/dr) (4), где t₀ – динамическое сопротивление сдвига, (Па).

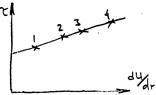
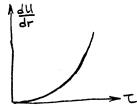
Степенные (Оствальдовские) ППЖ. t=k(dU/dr)ⁿ (5), где n – безразмерный показатель степени, k – показатель консистенции.

Зависимости (3), (5) находится по результатам эксперимента на вискозиметрах, чаще всего ротационных.

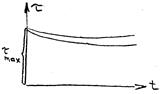
Тиксотропные (dU/dr) ₁> (dU/dr) _2, t=t(dU/dr; t)