Механизм процесса разрушения.
Переменная нагрузка приводит к усталостным трещинам.
Обычно очаг разрушения развивается на поверхности. В ней после деформации образуется наклепанная зона, где сначала появляются подповерхностные трещины. Однако растет только трещина, имеющая достаточную длину и острую вершину- это магистральная трещина. Продвигаясь вглубь, трещина образует глубокий и острый надрез. Рост трещины продолжается до излома. В некоторых публикациях отмечают, что для ряда материалов при обычном числе циклов повреждения начинаются с поверхности, а для некоторых, в случае сверхвысокого числа циклов- изнутри, причем их источниками являются включения.
Первые видимые трещины чаще всего возникают у впадин полос скольжения. Следовательно, зародышами усталостных трещин являются поверхностные впадины, которые по разным гипотезам могут появляться даже в том случае, если в начале процесса испытаний образца или работы детали их не было видно. Вследствие взаимного движения дислокаций за полный цикл деформации на поверхности образуются выступ и впадина, растущие по мере увеличения числа циклов. Существуют и другие гипотезы образования трещин.
Трещины тех или иных размеров, как уже говорилось, практически всегда имеются на поверхности детали, но могут зарождаться уже на начальных стадиях работы или испытаний.
В случае переменной пластической деформации аустенитных сталей имеют место локальные превращения парамагнитного аустенита в ферромагнитный мартенсит.
По мере увеличения числа циклов при любых напряжениях выше предела выносливости в образце последовательно идут следующие основные процессы [3]: 1) пластическая деформация; 2) зарождение трещин; 3) постепенное развитие некоторых из них и преимущественное распространение одной, главной трещины; 4) быстрое окончательное разрушение.
Движение дислокаций и образование линий скольжения в условиях повторно- переменных нагрузок при циклическом нагружении наблюдается даже при напряжениях меньше предела выносливости, который в свою очередь, как правило, ниже макроскопического предела упругости материала, т.е. напряжения, где заканчивается линейный участок диаграммы нагружения. Скольжение происходит в тех же кристаллографических плоскостях и направлениях, что и при статической деформации. Начинается пластическая деформация в благоприятно ориентированных зернах вблизи концентраторов напряжений.
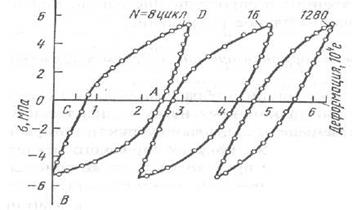
Развитие пластической деформации приводит к деформационному упрочнению, которое особенно существенно при малоцикловой усталости, когда величина действующих напряжений велика. (При малоцикловой усталости уже после первых циклов нагружения пластическая деформация заканчивается образованием трещин). Наглядной характеристикой деформационного упрочнения может служить ширина петли гистерезиса (рис. 2. 41).
|
Рис. 2. 41 .
Петли гистерезиса при циклическом нагружении монокристалла Al. Цифры у кривых- номер цикла [3].
Асимметрия связана с эффектом Баушингера. С увеличением числа циклов ширина W петли гистерезиса для материалов уменьшается.
Для монокристалла алюминия
W= AN-q, (2-29)
где q - коэффициент деформационного упрочнения; A - постоянная; N- - число циклов.
Материалы, у которых ширина W при мягком нагружении (нагружение с заданной амплитудой нагрузки) уменьшается, а максимальное напряжение цикла при жестком нагружении (с заданной амплитудой деформации) увеличивается, называются циклически упрочняющимися. Но есть и такие материалы, у которых ширина петли гистерезиса при мягком нагружении по мере увеличения числа циклов, наоборот растет, а максимальное напряжение цикла при жестком нагружении уменьшается. Такие материалы называют циклически разупрочняющимися. Наконец в ряде случаев ширина петли гистерезиса практически не меняется с ростом числа циклов. В этих случаях имеют место циклически стабилизирующиеся материалы.
Циклическое упрочнение или разупрочнение металлов и сплавов связано с особенностями их пластической деформации, зависящими от исходной структуры. В условиях симметричного растяжения- сжатия гладких образцов связь между амплитудами напряжений sа и eра подчиняется уравнению
sа= К’ (Deра/2)q’, (2-30)
где К’ - коэффициент циклической прочности; q’ - показатель циклического деформационного упрочнения.
Показатель q’ высок у металлов и сплавов с большой энергией дефектов упаковки (алюминий, никель, малоуглеродистые стали) и мал у материалов с низкой энергией дефектов упаковки (магний, a - латуни, нержавеющие аустенитные стали). Но вне зависимости от энергии дефектов упаковки, чистые металлы и однофазные сплавы, отличающиеся в отожженном состоянии высокой пластичностью и относительно низкой прочностью, относятся к циклически упрочняющимся материалам. После сильной холодной деформации эти же материалы ведут себя как циклически разупрочняющиеся. Циклическое разупрочнение наблюдается также у большинства высокопрочных сплавов, в частности, содержащих в структурах большое количество дисперсных выделений избыточных фаз.
Склонность материала к циклическому упрочнению или разупрочнению хорошо скоррелирована с отношением sв/ s0,2. Если оно меньше 1,2, то материал является циклически разупрочняющимся, если sв/s0,2³ 1,4 , то материал циклически упрочняется. При промежуточных значениях этого соотношения материал ведет себя как циклически стабилизирующийся.
Эти свойства обусловлены особенностями дислокационной структуры и формируются в условиях циклической деформации.
Критерием вязкого разрушения является неравенство [5]
si> sт ; s1= Sраз= f(s1/si), (2-31)
где si= 2-0,5[(sу- sx)2+ (sz- sx)2+(sx- sy)2+6(t2yz+ t2zz+ t2zy)]1/2- интенсивность напря-жений; s1- максимальное главное напряжение (нормальное) к площадке, когда нет касательных напряжений; sт- предел текучести при растяжении; Sраз - сопротивление разрушению деформированного металла.
Для пластического состояния закон Гука записывается в форме si= E’eI, где eI, - интенсивность деформации.
При растяжении гладкого образца j=s1/si» 1 и разрушению обычно предшествуют значительные пластические деформации. Концентраторы приводят к j=s1/si> 1 ик ограничению пластических деформаций перед возникновением трещин у вершины концентратора.
В случае объемного растяжения, когда s1=s2 = s3 величина si=0, eI, =0, j= ¥ и разрушение происходит хрупко сколом. Обычно таких случаев нет, а j= 2,6…3 и соответствует напряженному состоянию у вершины трещины. Здесь хрупкий отрыв происходит при очень ограниченной пластической деформации, когда si> sт ; s1> Sраз.
Разделив 2-е неравенство на первое, получим
j= s1/ si³ Sотр/ sт. (2-32)
Коэффициент j отражает жесткость напряженного состояния.
Последнее соотношение служит основой для установления условий наступления разрушения реального конструктивного элемента. Однако для этого необходимо определить значение j у вершины концентратора и учесть изменение напряженно- деформированного состояния при изменении нагрузки и по мере пластического деформирования.
Одним из основных критериев прочности в механике разрушения является критический коэффициент интенсивности напряжений (Кс). Это условная величина, зависящая от конкретного металла, толщины, конкретных характеристик структуры металла.
В случае нормального отрыва при отсутствии пластических деформаций напряжение вблизи трещин описывается уравнениями
sx= K1c(p r)1/2cos(q /2)[1- sin(q /2)sin(1,5q)], (2-33)
sx= K1c(p r)1/2cos(q /2)[1+ sin(q /2)sin(1,5q)], (2-34)
txy= K1c(p r)1/2sin (q /2)cos (q /2) cos(1,5q)], (2-35)
где r - удаление от вершины трещины; q- окружной угол.
Из-за различных нелинейных эффектов допускается использование этих формул для случаев, когда sсреднее£ 0,8 sт
Другими критериями разрушения являются:
- уровень выделения энергии при определенной скорости движения трещины;
- изменение температуры при образовании и распространении трещины.
Формы концентраторов напряжений разнообразны. Различаются в основном по углу a между плоскостями концентратора; радиусу r у вершины концентратора и виду напряженного состояния в плоскости АВСД (рис.2.42)

|
Рис. 2.42
Концентратор напряжений.
В общем случае коэффициент интенсивности напряжений описывается выражением
K1c = Ascp l1/2, (2-36)
где l - длина трещины; scp - среднее в ослабленном сечении напряжение; А- некоторый коэффициент.
Если a=0 , то
К1с=  0,5p1/2asscpr1/2, (2-37)
0,5p1/2asscpr1/2, (2-37)
где as = smax /scp
В механике разрушения используется критерий интенсивности выделения энергии (G1), означающий выделение энергии при подрастании трещины на единицу площади.

Рис.2.43. Изменение освобожденной энергии от подрастания трещины.
Величины К1с и G1 связаны для плоского напряженного состояния выражением
G1= K1c2/ E, (2-38)
Е - модуль упругости.
Уровень освобождающейся энергии при подрастании трещины связан с уровнем накопленной упругой энергии деформации у этой вершины, и чем больше Dl, тем больше G1 (см. рис. 2.43).
Работоспособность основного металла при монотонном
нагружении [5].
Для сохранения работоспособности изделия необходимо, чтобы размер трещины не превышал критического значения lкр, вызывающего снижение прочности до уровня допускаемого напряжения. Исключить отказы можно:
а) периодически проверяя материал с целью выявления растущей трещины и возможного ее удаления;
б) рациональным выбором материала, конструктивным и технологическим исполнением.
Поведение металла при нагружении сильно зависит от его способности к упрочнению. Это характеризуется показателем n в формуле
si= Aeni. (2-39)
По уровню прочности (низкий, средний, высокий) материалы разделяют по величинам s0,2, sв. Однако из-за различия удельного веса (g) и модуля упругости это оказывается недостаточным. В связи с чем введено понятие удельной прочности sвр/ g, деформативности s0,2/Е, накопленной упругой энергии s2в/ Е..В таблице 2-10 приведена классификация материалов с позиций прочности и деформативности
Табл.. 2- 10
| Материал | s0,2/Е | s0,2 , МПа | ||
| Стали | Сплавы Al | Сплавы Ti | ||
| Высокопрочн. | > 1/150 | > 1300 | > 400 | > 800 |
| Средн. прочн. | 1/150...1/300 | 1300...650 | 400...200 | 800....400 |
| Низк.прочн. | <1/300 | < 650 | <200 | <400 |
Из рис.2.44 видно, что по мере увеличения предела прочности sв, растет удельная прочность sв/g. Однако при этом повышается чувствительность к наличию концентратора напряжений, что может способствовать возникновению трещин.

|
Рис.2. 44 Зависимость удельной
прочности сплавов металлов
от разных факторов:
1- Mg; 2- Al; 3- Ti; 4- Fe.
Кроме того, с ростом предела прочности повышается уровень запасенной упругой энергии деформации s2в/Е, что увеличивает вероятность наступления нестабиль-ности возникшей трещины.
Совместное влияние этих факторов ограничивает использование материалов сверхвысокой прочности. Так, до сих пор весьма трудно использовать стали с sв ³ 2000МПа для тонкостенных сосудов, поскольку даже незначительные дефекты приводят к резкому снижению конструктивной прочности узла или изделия.
Определим, для примера, максимальную несущую способность стержня круглого сечения растягивающегося усилием X. В процессе растяжения после прохождения зоны текучести происходит увеличение сопротивления деформированию из-за упрочнения материала, но одновременно сопротивление снижается вследствие уменьшения поперечного сечения. В этом случае максимально возможная несущая способность достигается тогда, когда для дальнейшего увеличения деформации уже не требуется повышения усилия X. Этот момент соответствует образованию “шейки” на стержне.
Если полагать на диаграмме рис. 2.37 s= si , то зависимость интенсивности напряжений от относительной деформации можно описать уравнением [5]
si= s0,2 + A e ni пл . (2-40)
Для некоторых материалов это уравнение записывается в форме
Сталь 10 si= 210+ 306 e 0,21i пл ;
сталь 20 si= 260+ 368 e 0,18i пл;
сталь 40Х si= 570+ 422 e 0,07i пл.
С учетом отмеченного, для стали 10 нагрузка будет максимальной, при которой напряжение равно si= 210+ 306* 0,210,21= 210+ 220= = 430 МПа. Это имеет место в случае, если относительная пластическая деформация численно равна степени упрочнения. Здесь e i пл= n = 0,21.

|
Если взять цилиндрическую бочку, то максимальное рабочее давление здесь достигается раньше, чем наступит пластическая неустойчивость (в осевом направлении).
Рис. 2.45
Влияние несущей способности стенки цилиндрического сосуда от показателя степени упрочнения
Обычно показатели степени упрочнения ниже у более прочных металлов. Поэтому максимум напряжения для более прочного металла достигается при меньшей деформации (см.рис. 2.45).
В ряде случаев вводится понятие живучести (b)- это долговечность детали от момента появления первой трещины длиной 0,5...1,0 мм до окончательного разрушения. Живучесть может иметь значения b= 0,1...0,9.
Введен также для жаропрочных сталей критерий ползучести, имеющий особое значение для теплообменных аппаратов.
Это деформация при Т> 400°C под нагрузкой. Предел ползучести это напряжение при заданной скорости деформации. Так, сталь 22К имеет предел ползучести s 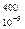 = 132МПа. Здесь скорость деформации составляет 10-5%/час. Предел длительной прочности- это максимальное напряжение, при котором металл разрушается за определенное время при постоянной температуре, например s
= 132МПа. Здесь скорость деформации составляет 10-5%/час. Предел длительной прочности- это максимальное напряжение, при котором металл разрушается за определенное время при постоянной температуре, например s  = 139МПа. Здесь нижний индекс обозначает время- 104 часов.
= 139МПа. Здесь нижний индекс обозначает время- 104 часов.
Однако, если принимать меры только для увеличения предела прочности, твердости и других прочностных характеристик, то это может оказаться недостаточным для повышения сопротивления усталости. Упрочнение будет приводить к затруднению зарождения трещины. Если же при этом существенно снизится пластичность, то распространение уже имеющейся трещины будет облегчено. Поэтому более правильно ориентироваться на корреляцию с каким-либо сочетанием прочностных и пластических свойств [3]
s-1= 0,26sв{1+ 0,5 ln[(1+y)(1-yb)(1+ yb)-1(1- y)-1]}, (2-41)
где y - конечное относительное сужение; yb - наибольшее равномерное сужение.
Сочетания повышенных прочностных и пластических свойств можно добиться легированием твердого раствора, измельчением зерна и субструктуры, созданием композиционных материалов.
По мнению [3] характеристики сопротивления усталости несколько менее чувствительны к структурным изменением, чем многие другие свойства.
Реакция материала на надрез [5]
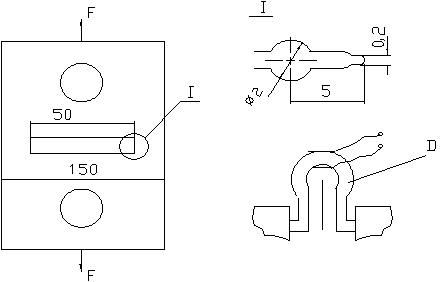
Определять конструктивную прочность нагружением готового изделия слишком дорого и трудоемко. Чаще всего это делают на моделях. При этом реакция материала на наличие несплошностей характеризуют размером пластической зоны и значением пластической деформации в разрезе у вершины дефекта к моменту страгивания трещины. В качастве модели, например, используют образцы, показанные на рис. 2.46.
Вначале пластической деформации в вершине трещиноподобного дефекта преобладает упругая составляющая перемещения
|
Рис. 2.46.
Образцы для испытаний и схема измерений с помощью тензодатчика (D)
Этот процесс иллюстрируется рис. 2.47, где z- перемещение кромок надреза.

|
Рис. 2. 47.
Изменение напряжения в зависимости от перемещения кромок надреза
При возрастании силы F зона пластической деформации начинает интенсивно расширяться и кривая s(z) отходит от прямой. Точка Q соответствует страгиванию трещины. Страгивание трещины начинается не одновременно по всему дну, а с середины толщины в точке А образца (см. рис. 2 .48) .

|
Рис. 2.48
Появление и распространение трещины шириной dтр в зоне точки А.

|
Рис. 2. 49
Экспериментальные зависимости изменения напряжения от величины перемещения кромок надреза:
а) для образца из углеродистой стали ст 3пс толщиной 8 мм с несквозным надрезом;
б) для образца из нержавеющей стали 03Х11Н10М2Т;
в) в общем случае.
Затем она тунеллирует вдоль надреза и в последствии развивается по всей ширине. Такое движение объясняется соответствующим напряжен-ным состоянием.
Если надрез не сквозной, то трещина растет по толщине, выходя на противоположную поверхность образца.
На рис. 2.49 показаны результаты испытаний различных образцов, а также интегральная зависимость
Из этих графиков четко видна разница развития трещины в разных сталях.
Если при деформации в зоне I страгивается трещина, то она становится нестабильной. Это хрупкое разрушение.
Если же страгивания трещины в зоне I не произошло, то в зоне II происходит затупление ее очертаний, и трещина становится стабильной.
В зоне III имеет место сильное притупление очертаний трещины, а ее превращение в сквозную происходит стабильно. Разрушение в этом случае является вязким.
Механические свойства при динамических испытаниях.
Изложенные особенности разрушения выявляются при следующих динамических испытаниях:
Ударная вязкость
Это работа К удара, отнесенная к начальной площади s0 поперечного сечения образца в месте концентратора
KC= K/s0.
F
¯

Рис.2 .50. Схема определения ударной вязкости
Образцы имеют концентраторы вида U (изображен на рис. 2.50), V, T (для усталостных трещин). В зависимости от используемых образцов ударная вязкость тогда обозначается, как KCU, KCV, KCT.
Ударная вязкость включает работу зарождения трещины (аз) и работу, затрачиваемую на распространение вязкой трещины (ар), т.е.
KCU= аз+ ар.
Чем больше ар , тем меньше возможность внезапного разрушения.
Порог хладоломкости.
Определяется при испытаниях ударным изгибом надрезанных образцов для разных температур. Порог определяют по виду излома, где оценивают количество матовой волокнистой составляющей. Должно быть не менее 50%. Этот критерий называют также критической температурой хрупкости.
Дата добавления: 2015-02-19; просмотров: 1406;
