Модель общего равновесия Вальраса. Закон Вальраса

Первым экономистом, построившим математическую модель с помощью системы уравнений для доказательства возможности существования общего равновесия, был швейцарский экономист Леон Вальрас (1834-1910). Он предположил, что народное хозяйство состоит из 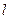потребителей, использующих n взаимосвязанных благ, производство которых ведется с применением m различных факторов производства. При условиях:

- данности функций полезности каждого потребителя и его бюджета,

- равенства бюджета потребителя ценности его факторов производства,

- фиксированности объема его факторов производства (абсолютной неэластичности их предложения), можно построить функцию спроса i-го потребителя на j-е благо:

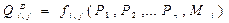(6),

где ,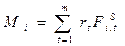

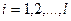
M_i – бюджет i-го потребителя,

P_j , r _t - соответственно цены благ и факторов, j = 1,2,..n, t=1,2,...m,

F^S _{i, t} - заданный объем t-го фактора, принадлежащего i-му потребителю.

В целях упрощения предположим, что каждая фирма производит только один вид благ. При заданной технологии и известных ценах на блага и факторы производства фирма, максимизирующая прибыль, формирует функцию предложения блага и функцию спроса на факторы. Сумма предложений всех фирм, производящих одно и то же благо, образует отраслевое предложение :

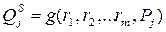(7),

Суммарный спрос этих фирм на факторы составляет отраслевой спрос на каждый из факторов:

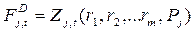(8)

На основе функций (6)-(8) строится микроэкономическая модель общего равновесия, состоящая из трех групп уравнений:

1.условия равновесия на рынке благ:

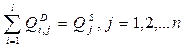(9)

2.условия равновесия на рынках факторов производства:

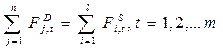(10)

3.бюджетные ограничения фирм на рынке совершенной конкуренции в виде равенства общей выручки общим затратам:

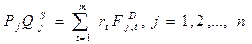(11)

Система уравнений (9)-(11) содержит 2n+m неизвестных и столько же уравнений. Но независимыми являются только 2n+m-1 уравнение. Это связано с бюджетным ограничением потребителей, из-за которого суммарный избыточный спрос любого потребителя равен нулю.

Допустим, что существуют только 2 рынка благ и 1 рынок факторов. Бюджетное ограничение (уравнение) 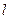-го потребителя имеет вид:

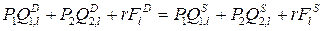(12)

Это равенство говорит о том, что расходы 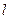-го потребителя (левая часть) должны равняться его доходам от продажи имеющихся у него благ и факторов производства (правая часть).

Или: 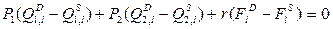(13)

В круглых скобках - избыточный спрос 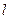-го потребителя на каждом из рынков, т.е. равенство суммарного избыточного спроса нулю у любого потребителя есть лишь иная форма представления его бюджетного ограничения. Просуммируем бюджетные уравнения всех участников рыночных сделок:

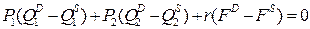(14)

Из равенства (13) следует, что если система цен P₁ , P _{2 ,} r обеспечивает равновесие на любых двух рынках, то равновесие будет и на третьем. Этот вывод, верный для любого числа рынков, носит название закона Вальраса.