Теоретическое введение. Трение в подшипниках качения имеет место:

Трение в подшипниках качения имеет место:

– между телами качения и внутренним и наружным кольцами;

– между телом качения и сепаратором;

– между шариками и кольцами из-за различия в скоростях на дуге контакта общих точек шарика и кольца.

Трением качения называется сопротивление, возникающее при перекатывании одного тела по другому. Сопротивление перекатывания зависит от упругих свойств материалов, шероховатости, кривизны соприкасающихся поверхностей и величины сжимающей силы, т.е. сопротивление качению вызвано деформацией поверхности соприкосновения (рис. 8.1).

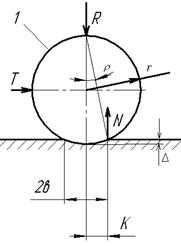
Рис. 8.1. Силы в зоне контакта при перекатывании тел

На рис. 8.1 изображен цилиндр, нагруженный силой R. В неподвижном цилиндре 1 сила R уравновешивается равнодействующей сил реакции смятия на площадке шириной 2в. При возникновении силы Т наличие внутреннего трения в материале вызывает в зоне деформации несовпадение линии действия нагрузки R и реакции вследствие упругого гистерезиса, что вызывает асимметрию эпюры деформаций относительно максимума и смещение этого максимума в сторону движения на величину .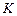

Эта величина называется плечом силы трения качения. Она же зовется и коэффициентом трения качения и измеряется в единицах длины [мм].

При приложении движущей силы Т к цилиндру момент трения качения 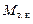уравновешивается моментом движущей силы

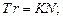
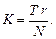(1)

Отношение 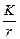– в технических расчетах называют приведенным коэффициентом трения качения, а угол 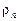– приведенным углом трения.

Из рис. 8.1 следует

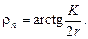
Для стальных шариков или роликов, катящихся по закаленным обоймам при частоте поверхности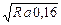

К = 0,008 ¸ 0,01.

Трение между телом качения и сепаратором – обычное трение скольжения между движущейся и неподвижной поверхностями.

Возникновение трения между шариком и кольцом объясняется разностью линейных скоростей общих точек контакта шарика и кольца 2 в точках А и Б (рис. 8.2).

Линейная скорость 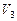точки А – общая для шарика и кольца. При перекатывании шарика по кольцу без скольжения угловая скорость шарика в точке А в этом случае определяется как

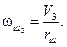
Линейная скорость кольца 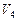в точке Б увеличивается вследствие увеличения радиуса кольца на величину ∆₁. Угловая скорость шарика, определяемая для точки А должна быть

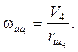
Поскольку радиус шарика 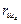относительно мгновенного центра уменьшается, скорость 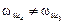, что и является причиной скольжения.

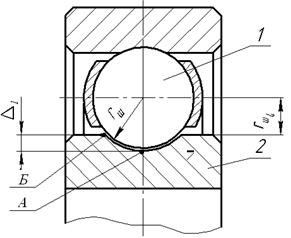
Рис. 8.2. Зоны трения