Законы Кирхгофа

Первый закон Кирхгофа. Алгебраическая сумма токов, сходящихся в узле, равна нулю:

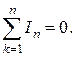
Ток, подходящий к узлу, берется со знаком «+», отходящий от узла, - со знаком «-».

Второй закон Кирхгофа. Алгебраическая сумма падений на­пряжения в любом замкнутом контуре равна алгебраиче­ской сумме ЭДС в этом контуре:

.

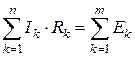В каждую из сумм соответствующие слагаемые входят со знаком «+», если их направления совпадают с направлением обхода контура, и со знаком «-», если их направления не совпадают с ним.

Для составления уравнений по законам Кирхгофа необходимо: выбрать произвольно направления токов в ветвях и выбрать положительные направления обхода контуров.

Количество уравнений определяется количеством неизвестных токов.

Число уравнений по первому закону Кирхгофа на единицу меньше числа узлов:

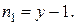
По второму закону Кирхгофа составляется недостающее число уравнений, равное числу независимых контуров или ветвей без источников тока ( 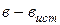) за вычетом числа уравнений, составленных по первому закону:

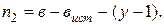
При составлении уравнений по второму закону независимые контуры выбираются так, чтобы в каждый из них входила новая ветвь, исключая ветви с источниками тока.

ПРИМЕР 1.4.1.

Дано: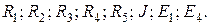

Cоставить уравнения по законам Кирхгофа для определения неизвестных токов.

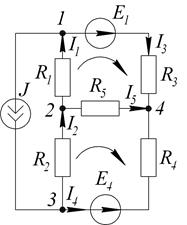
Решение:

Произвольно выбираем направление токов в ветвях и направление обхода контуров. В схеме шесть ветвей. Необходимо составить систему из 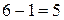уравнений.

По первому закону составляем 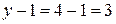уравнения.

Для узла 1: .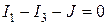

Для узла 2: .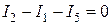

Для узла 3: .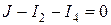

Недостающие два уравнения составляем по второму закону Кирхгофа:

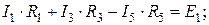
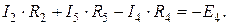
ПРИМЕР 1.4.2

Дано: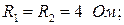

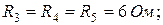
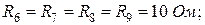
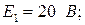
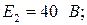
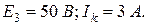
Составить уравнения по законам Кирхгофа и определить токи в ветвях.

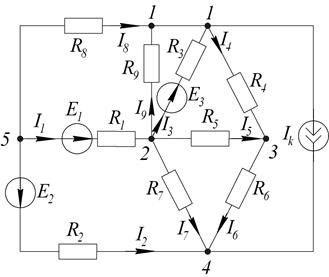
По первому закону составляем 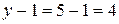уравнения.

Для узла 1: .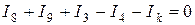

Для узла 2: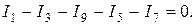

Для узла 3: .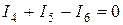

Для узла 4: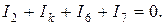

Недостающие пять уравнений составляем по второму закону Кирхгофа для явно выраженных контуров:

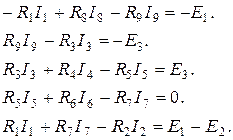
Запишем эти уравнения в виде удобном для записи их в матричной форме

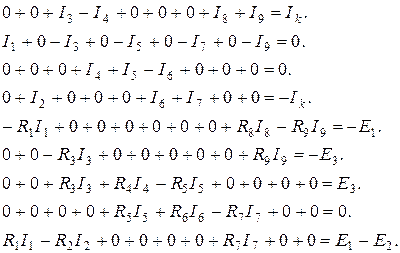
Матричная форма записи системы уравнений: R×I=E.

Порядок решения заданной системы уравнений:

1. Установите режим автоматических вычислений.

2. Введите матрицу системы и матрицу - столбец правых частей.

3. Вычислите решение системы по формуле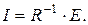

4. Проверьте правильность решения умножением матрицы системы на вектор - столбец решения.

5. Найдите решение системы с помощью функции lsolve и сравните результаты вычислений.

Ниже приведен фрагмент решения этой системы уравнений в программе Mathcad.

Зададим матрицу системы 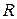и матрицу - столбец 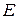правой части.

Надо найти матрицу - столбец неизвестных токов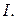

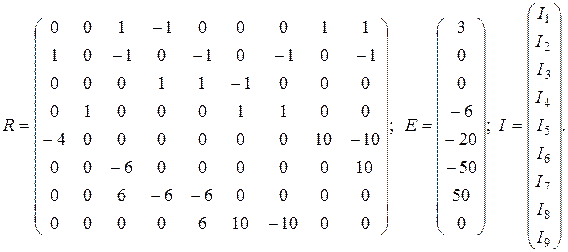
Вычислим решение системы по формуле :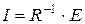

.

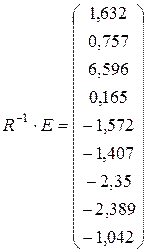Где: ; ; ; ; ; ; ; ; .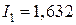

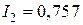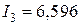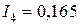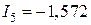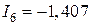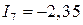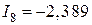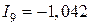Решим систему с помощью функции lsolve и сравним результат с решением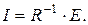

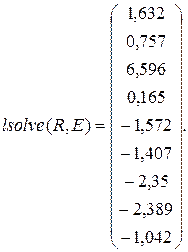
Заданная система уравнений решена правильно.