Схема замещения и векторная диаграмма реальной катушки с магнитопроводом
Обмотка реальной катушки с сердечником обладает активным сопротивлением 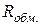 . Магнитный поток является векторной суммой основного потока в магнитопроводе и потока рассеяния
. Магнитный поток является векторной суммой основного потока в магнитопроводе и потока рассеяния
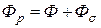 .
.
Величина основного потока 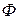 определяется свойствами материала магнитопровода. Поток рассеяния
определяется свойствами материала магнитопровода. Поток рассеяния 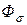 зависит от конструкции обмотки, взаимного расположения витков, их сечения и составляет
зависит от конструкции обмотки, взаимного расположения витков, их сечения и составляет 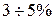 от основного потока. Потокосцепление рассеяния пропорционально току:
от основного потока. Потокосцепление рассеяния пропорционально току:
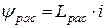 ,
,
где 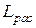 - индуктивность рассеяния обмотки.
- индуктивность рассеяния обмотки.
С учетом активного сопротивления обмотки 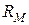 и потокосцепления рассеяния
и потокосцепления рассеяния 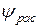 напряжение на входе катушки
напряжение на входе катушки
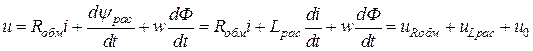 .
.
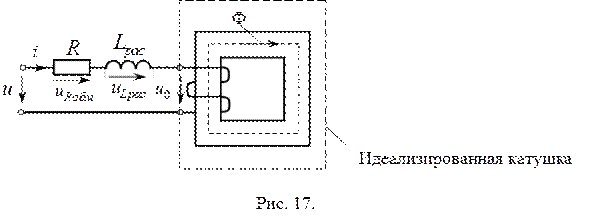
Таким образом, реальную катушку с магнитопроводом можно представить схемой замещения в виде последовательного соединения 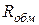 ,
, 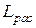 и идеализированной катушки (рис. 17). У идеализированной катушки обмотка не имеет сопротивления и рассеяния. Свойства идеализированной катушки зависят только от параметров магнитопровода и режима его намагничивания.
и идеализированной катушки (рис. 17). У идеализированной катушки обмотка не имеет сопротивления и рассеяния. Свойства идеализированной катушки зависят только от параметров магнитопровода и режима его намагничивания.
Напряжение 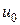 уравновешивает ЭДС индукции идеализированной катушки
уравновешивает ЭДС индукции идеализированной катушки 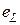 и опережает магнитный поток на
и опережает магнитный поток на 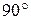 .
.
Переход к эквивалентным синусоидам тока дает возможность записывать все соотношения в комплексной форме и пользоваться векторными диаграммами.
Комплексное действующее значение входного напряжения запишется в виде
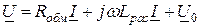 .
.
Схема замещения идеализированной катушки зависит от параметров магнитопровода и режима его намагничивания. Если предположить, что магнитопровод изготовлен из ферромагнетика с линейной зависимостью 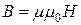 , то
, то 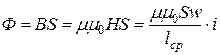 и выражение напряжения на входе катушки:
и выражение напряжения на входе катушки:
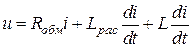 ,
,
где 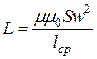 - индуктивность идеализированной катушки.
- индуктивность идеализированной катушки.
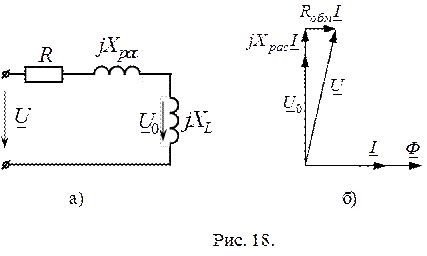
Схема замещения реальной катушки для этого случая представлена на рис. 18.а, соответствующая ей векторная диаграмма на рис. 18.б.
При учете потерь, обусловленных гистерезисом и вихревыми токами в сердечнике (зависимость 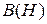 петлевая), ток в обмотке катушки опережает магнитный поток на угол потерь
петлевая), ток в обмотке катушки опережает магнитный поток на угол потерь 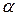 и может быть разложен на две составляющие.
и может быть разложен на две составляющие.
Активная составляющая тока совпадает по фазе с напряжением 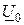 и называется током потерь
и называется током потерь 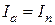 , она определяется через мощность потерь в стали.
, она определяется через мощность потерь в стали.
Реактивная составляющая тока отстает от напряжения 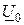 на
на 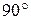 , называется током намагничивания
, называется током намагничивания 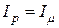 и определяется из закона полного тока.
и определяется из закона полного тока.
В комплексной форме ток 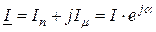 .
.
Комплексное полное сопротивление идеализированной катушки:
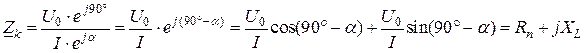 .
.
Заменив идеализированную катушку последовательным соединением 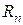 и
и 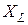 получаем схему замещения реальной катушки для рассматриваемого случая (рис. 19,а)
получаем схему замещения реальной катушки для рассматриваемого случая (рис. 19,а)
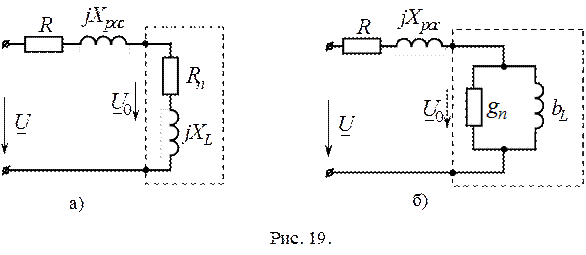
Переход от последовательной схемы замещения идеализированной катушки к параллельной (рис. 19,б) проводится по формулам:
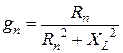 ;
; 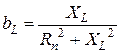 .
.
Векторная диаграмма реальной катушки индуктивности с магнитопроводом, имеющим петлевое намагничивание представлена на рис. 20.
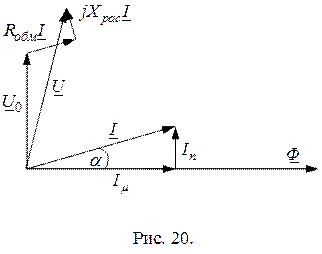
При расчетах полное сопротивлении катушки индуктивности с магнитопроводом находят по закону Ома 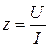 . Оно определяется главным образом индуктивным сопротивлением
. Оно определяется главным образом индуктивным сопротивлением 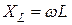 (
( 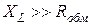 ).
).
Приближенно, пренебрегая активным сопротивлением обмотки и рассеянием магнитного потока, можно определить индуктивность 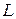 из соотношения
из соотношения 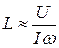 или вычислить по потокосцеплению:
или вычислить по потокосцеплению:
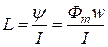 , где
, где 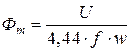 .
.
Эквивалентное активное сопротивление катушки определяется по значению активной мощности и току:
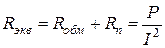 .
.
Пример.Катушка со стальным сердечником подключена к источнику синусоидального напряжения 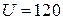 В, частотой
В, частотой 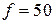 Гц. Действующее значение тока в обмотке катушки
Гц. Действующее значение тока в обмотке катушки 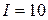 А, мощность потерь
А, мощность потерь 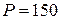 Вт. Сопротивление обмотки
Вт. Сопротивление обмотки 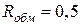 Ом.
Ом.
Определить параметры схемы замещения нелинейной катушки. Магнитным рассеянием пренебречь.

Решение. Мощность потерь в катушке с магнитопроводом состоит из тепловой мощности в обмотке (в меди) и потерь в магнитопроводе (в стали):
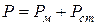 .
.
Потери в обмотке 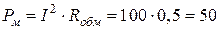 (Вт).
(Вт).
Потери в стали 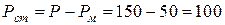 (Вт).
(Вт).
Коэффициент мощности 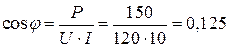 .
.
На векторной диаграмме (рис. 21,б) в треугольнике напряжений со сторонами 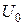 ,
, 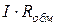 ,
,  угол
угол 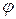 находится против стороны
находится против стороны 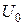 , следовательно,
, следовательно,
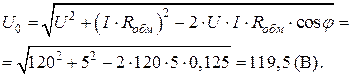
Активная и реактивная составляющие тока катушки:
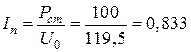 (А),
(А),
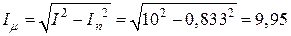 (А).
(А).
Сопротивления активной и индуктивной ветвей схемы замещения:
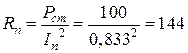 (Ом),
(Ом),
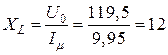 (Ом).
(Ом).
Откуда, 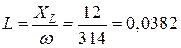 (Гн).
(Гн).
Дата добавления: 2015-01-13; просмотров: 7731;
