Расчет неразветвленной магнитной цепи по заданному потоку

Рассмотрим последовательность расчета магнитной цепи изображенной на рисунке 8.

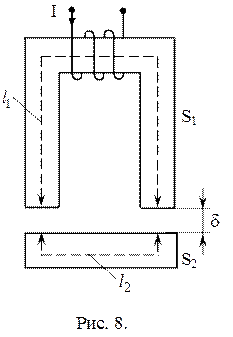
Дано: геометрические размеры магнитной цепи в мм; магнитный поток Ф или индукция 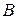в каком-либо сечение; кривая намагничивания .

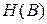Определить: МДС .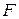

Задачу решаем, применив закон полного тока .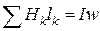

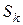1. Разбиваем магнитную цепь на участки постоянного сечения и определяем длинны (м) участков и площади их поперечного сечения (м²). Длины участков берем по средней силовой линии. Величина воздушного зазора равна 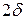(м).

, , , ,

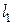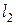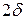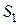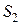
2. Исходя из постоянства магнитного потока 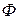( ), пренебрегая потоком рассеяния, по заданному потоку находим магнитную индукцию 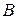(Тл) на участках:

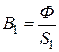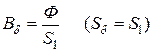, , . (1)

3. По кривой намагничивания определяем напряженность магнитного поля 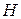(А/м) в магнитопроводе:

, .

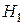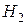Магнитная проницаемость воздуха 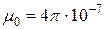Гн/м и напряженность магнитного поля в зазоре рассчитывается по формуле

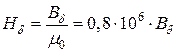. (2)

4. Подсчитываем сумму падений магнитного напряжения и определяем МДС:

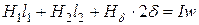. (3)

Между расчетами нелинейных магнитных цепей с постоянными МДС и расчетом нелинейных электрических цепей постоянного тока нетрудно установить аналогию.

Если в уравнении (3) заменить значение напряженности магнитного поля значениями индукции, получим:

,

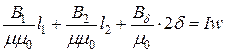с учетом (1):

,

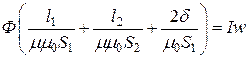где 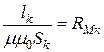- магнитное сопротивление к-го участка магнитопровода. Оно нелинейно, т.к. зависимость 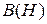нелинейна.

С учетом этого рассматриваемой магнитной цепи соответствует эквивалентная схема замещения (рис. 9), для анализа которой можно пользоваться всеми методами анализа электрических цепей с нелинейными сопротивлениями.

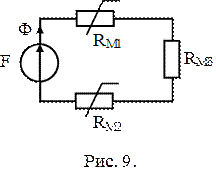
Обратная задача.Считая известной м.д.с. F , определим магнитный поток Ф.

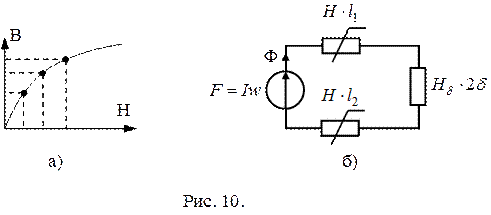
Произвольно задаемся магнитным потоком Ф и определяем магнитную индукцию В

,

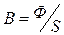далее по заданной кривой намагничивания (рис. 10, а) определяем напряженность Н.

При заданном значении Ф определяем F по второму закону Кирхгофа (рис. 10, б).

.

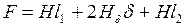Производим аналогичный расчет для нескольких точек. Строим зависимость Ф = f(F). Истинное значение Ф определяем по точке пересечения полученной кривой и заданной м.д.с. F (рис. 11).

Пример. В неразветвленной магнитной цепи с длинной средней линии 0,4 м и воздушным зазором 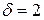мм необходимо создать магнитную индукцию 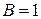Тл. Магнитопровод выполнен из электротехнической стали 1512. Определить напряженность поля в магнитопроводе и воздушном зазоре, ток намагничивающей обмотки с числом витков .

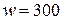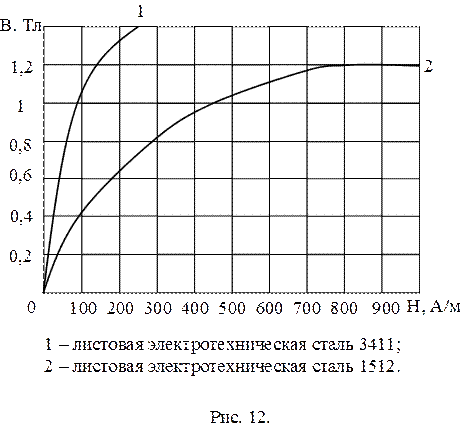
Решение. Напряженность магнитного поля в воздушном зазоре 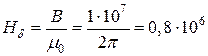А/м. По кривой намагничивания (рис. 12) находим напряженность поля магнитопровода 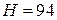А/м.

Намагничивающая сила обмотки по закону полного тока

А.

Следовательно, ток обмотки 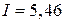А.

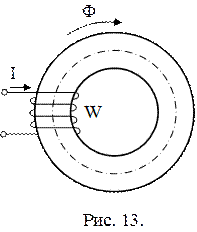
Пример. На кольцевой однородный магнитопровод (рис. 13) намотана намагничивающая обмотка с числом витков 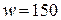. Наружный диаметр кольца мм; внутренний диаметр 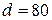мм, его поперечное сечение квадратное. Определить ток и магнитодвижущую силу обмотки, необходимые для создания в магнитопроводе потока Вб. Чему равно магнитное сопротивление магнитопровода, если он выполнен из электротехнической стали 3411?

Решение. Ток обмотки рассчитывается по формуле 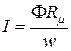. Для нахождения 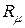необходимо определить индукцию 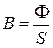, где сечение 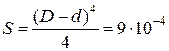м². Следовательно, индукция 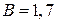Тл. Воспользовавшись рис. 4 для стали 3411, можно найти напряженность магнитного поля А/м.

Искомое магнитное сопротивление определяется из соотношения . Длина средней силовой линии в данном случае м. Найдя ток 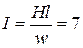А, можно определить намагничивающую силу 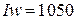А и магнитное сопротивление 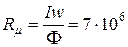Гн^-1.