Через любую точку на графике можно провести кривую безразличия.

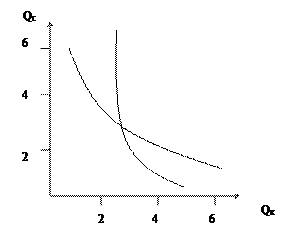
2. Кривые безразличия никогда не пересекаются. Для доказательства этого обычно используют метод доказатель­ства от противного. Допустим, что кривые безразличия пересекаются (рис.2).

С

А

В

Обозначим на этих кривых три точки А, В, С. Точка С будет точкой пересечения. Тогда наборы А и С, С и В будут иметь одинаковую полезность, так как находятся на одной кривой безразличия. Однако согласно правилу транзитивности набор А должен быть по полезности таким же, как и набор В, но этого не может быть, так как набор В включает в себя большее количество двух товаров, чем набор А, следовательно, он более пред­почтителен. Наше допущение о пересечении кривых ока­залось неверным.

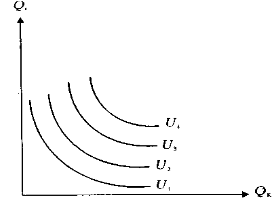
3. Если мы нанесем на графике несколько кривых безразличия, то получим карту кривых безразличия, на которой кривые, более удаленные от начала координат, соответствуют большей полезности потребляе­мых благ Q1 и Q2(рис.3).

4. Кривые безразличия имеют отрицательную направ­ленность. Это можно объяснить следующим. Чтобы увели­чить количество одного товара в потреблении при сохра­нении той же общей полезности, нужно пожертвовать количеством другого товара и наоборот, уменьшая один товар в потреблении, увеличиваем другой, чтобы получить то же удовлетворение. Замещение одного блага другим позволяет сохранить уровень полезности. Потеря одного блага компенсируется потреблением другого.

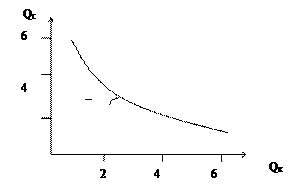
5. Кривые безразличия имеют вогнутый вид (иногда говорят выпуклый по отношению к началу координат). Это свойство кривых безразличия можно объяснить, если рас­смотреть, как именно происходит замещение одного блага другим (рис.4).

	Рис.4.Вогнутость кривой безразличия

Из нашего примера видно, что пока конфет мало в потреблении, Алеся готова отказаться от значительного количества сока (3 единицы сока за 1 единицу конфет), но по мере возрастания конфет в потреблении и уменьшения сока ценность сока возрастает, а конфет — падает (за четвертую порцию конфет Алеся согласна пожертвовать только 0,5 порциями сока). Это значит, что предельная полезность сока относительно конфет стала выше. Вместо понятия "предельная полезность" ординалисты использу­ют понятие "предельная норма замещения".

Отдельные случаи конфигурация кривых безразличия.

Допустим, что все нарисованные кривые безразличия отражают набор из двух товаров, но для разных потреби­телей: кинофильмы (вертикальная ось) и театральные спектакли (горизонтальная ось).

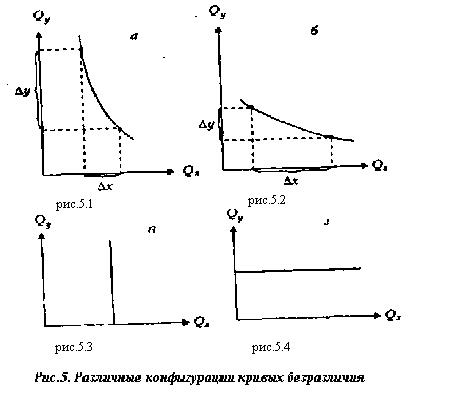
Как видим, для первого потребителя (рис.5.1) театральные спектакли предпочтительнее, он готов пожер­твовать значительным количеством кинофильмов ради одного спектакля (предельная норма замещения высока). Второй потребитель (рис.5.2) предпочитает кинофиль­мы, меньше любит театр, поэтому кривая безразличия более пологая (предельная норма замещения низка). Тре­тий потребитель (рис.5.3) — заядлый театрал, он посещает только театр и не ходит в кино. Предельная норма замещения театра кинофильмом равна 0. И, наконец, четвертый потребитель (рис.5.4) не любит театр и ходит только кино. Предельная норма замещения кинофильма театральной пьесой для него равна 0. Кроме того, кривые безразличия отличаются и в случаях с совершенными субститутами и совершенно комплиментарными благами (рис.6).

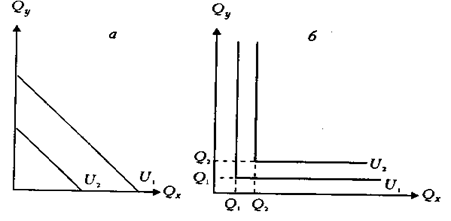
Кинофильмы и театральные постановки могут быть для некоторого зрителя совершенными субститутами (рис.6,а), т.е. он оценивает их полезность одинаково. Это зна­чит, что каждый кинофильм может без ущерба быть заме­нен театральной пьесой и наоборот. В этом случае предель­ная норма замещения всегда равна 1, а кривая безразличия выглядит как прямая с наклоном, равным 1. В качестве абсолютных комплиментарных благ (рис.6,б) рассмот­рим автомобили и номерные знаки. Они не могут замещать друг друга, поэтому предельная норма замещения каждого товара по отдельности равна 0. Их потребление возможно только вместе, причем два автомобиля требуют двух номер­ных знаков, три — трех и т.д. Поэтому кривые безразличия для таких товаров отличаются. Уменьшение предельной нормы замещения означает, как уже отмечалось, уменьшение предельной полезности х и соответственно увеличение предельной полезности у. MRS можно представить как отношение предельных полезностей х и у:

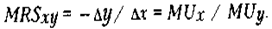
Предельная норма замещения благ.

Предельная норма замещения. Предельной нормой замещения товаром х товара у (MRSxy) называют количе­ство товара у, от которого потребитель отказался бы, чтобы получить дополнительную единицу товара х, оставаясь при этом на кривой безразличия: MRSxy = — y / х.

В нашем примере увеличение конфет в потреблении Алеси сопровождалось уменьшением предельной нормы за­мещения сока конфетами: MRS1 = 3, MRS2 = 1, MRS3= 0,5.

Вогнутость кривой безразличия объясняется уменьше­нием предельной нормы замещения. В каждой точке на кривой безразличия предельная норма замещения равна наклону кривой. Этот наклон можно обнаружить, если провести касательную к каждой точке. Угол наклона каса­тельной к горизонтальной оси координат при увеличении товара х в потреблении уменьшается. Уменьшение наклона делает кривую вогнутой.

Чем можно объяснить выпуклость кривой безразличия, то есть убывание MRS? Ответ заключается в том, что субъективная готовность потребителя к замещению продукта на другой продукт зависит от начальных количеств продукта. Это значит, что при перемещении вниз по кривой, потребитель будет готов отказаться от меньшего количества одного продукта, в порядке компенсации за приобретение другого товара в результате получаем кривую с убывающим наклоном, то есть выпуклую по отношению к началу координат. Иначе можно сказать еще, что MRS снижается по мере продвижения вправо вдоль кривой безразличия.

Предельная норма замещения в ординалистской теории полезности те же функции, что и предельная полезность в кординалистской теории.