Выработка оптимальной стратегии в игровой ситуации

Игрок делает ставку в размере $9,00 и получает возможность четыре раза бросить игровую кость, имеющей на своих гранях числа 1, 2, 3, 4, 5 и 6. Игрок может закончить игру после любого броска, забрав выигрыш, равный удвоенному числу, выпавших во время последнего броска очков. Стоит ли играющему соглашаться на такие условия игры? При положительном ответе разработать стратегию поведения игрока. Попробуем разобраться в описанной игровой ситуации. Прежде всего, представим условия игры в виде таблицы приложения MS Excel на Рис.7.

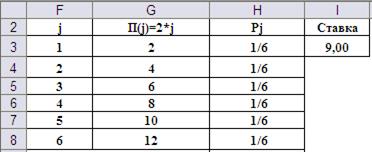
Рис.7. Представление исходных данных в приложении MS Excel.

Очевидно, что если в первом броске выпадет 6 или 5, то игру можно заканчивать, т.к. выигрыш будет превышать сделанную ставку. Правда, во втором случае можно понадеяться на выпадение 6 в последующих бросках. При выпадении в первом броске меньшего, чем 5 числа очков можно, надеясь наудачу в последующих попытках, продолжить игру. С другой стороны, если игрок дошёл до четвёртой попытки, то окончание игры будет безусловным и, возможно, при выпадении малого числа очков, игрок пожалеет, что не прервал игру на более удачных предыдущих попытках.

Решение. Очевидно, что ситуация носит вероятностный характер. Поэтому принятие решения: соглашаться или нет на предложенные условия игры, возможно лишь при оценке среднего выигрыша. Поставленная задача относится к задачам вероятностного динамического программирования. Они решаются в соответствии с алгоритмом обратной прогонки [1-3].

Для функции Беллмана введём обозначение 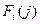, означающее средний выигрыш на i-ом шаге при условии, что выпало j очков. Очевидно, её нужно вычислять как максимум между текущим выигрышем при выпадении j очков 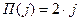и средним значением функции Беллмана на последующем шаге 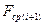, т.е.

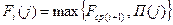
Если всего шагов n, то очевидно, что:

,

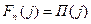т.к. у последнего шага последующих шагов нет. Для формализации и однотипности действий на каждом шаге удобно считать, что .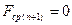

Итак, алгоритм обратной прогонки.

Шаг 1-ый, i=4. Его результат представлен таблицей, рассчитанной в MS Excel (Рис.8)

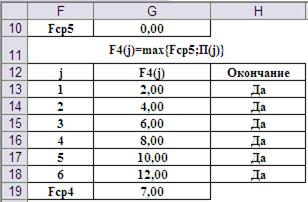
Рис.8. Результат первого шага вычисления функции Беллмана.

Данные были автоматически сформированы при вводе в ячейки рабочего листа формул, представленных на Рис.9.

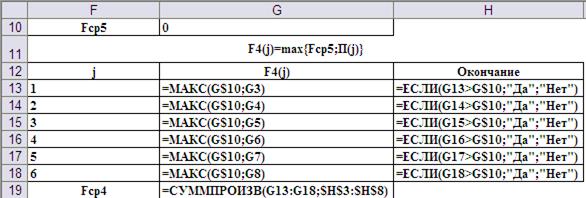
Рис.9. Ввод формул для реализации первого шага.

Шаг 2-ой, i=3. Его результаты и ввод формул для реализации представлены на Рис.10 и Рис.11, соответственно.

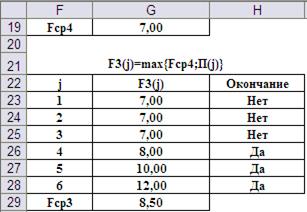
Рис.10. Результат второго шага вычисления функции Беллмана.

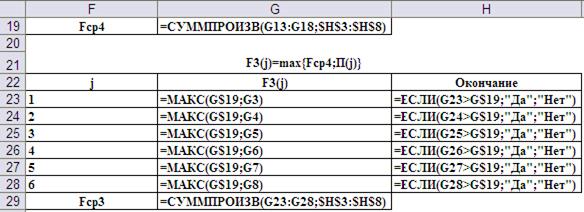
Рис.11. Ввод формул для реализации второго шага.

Выполнение третьего и четвёртого шагов показаны на Рис.12 (результаты) и Рис.13 (формулы).

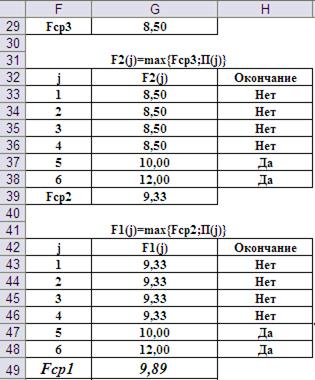
Рис. 12. Результаты расчётов на третьем и четвёртом шагах.

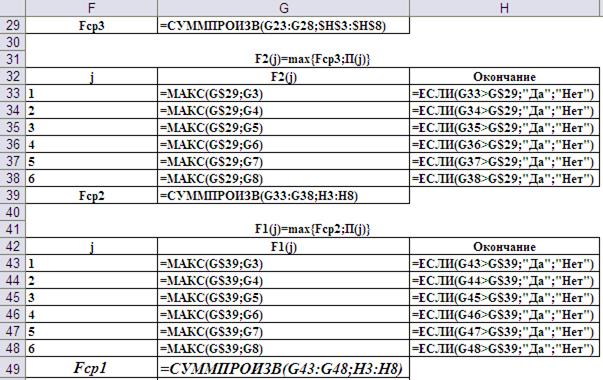
Рис. 13. Ввод формул для выполнения третьего и четвёртого шагов.

Итак, в результате реализации алгоритма обратной прогонки получили ответы на оба поставленных вопроса задачи. Во-первых, т.к. F_cp1=9,89 превышает сделанную ставку, равную 9, то условия игры могут быть приняты. Во-вторых, оптимальная стратегия действий игрока на каждом шаге представлена в третьих столбцах таблиц результатов на каждом шаге. При игре их надо просматривать в прямом, а не в обратном, порядке.

Организация рабочего листа в приложении MS Excel позволяет ответить и ряд других вопросов. Например, нечистые на руку организаторы игрового бизнеса предлагают играть «краплёными» костями с вероятностью выпадения граней, представленных в таблице:

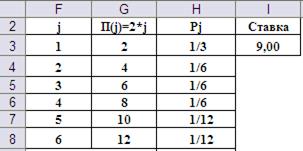
Указанные в таблице вероятностные характеристики игральных костей можно получить за счёт смещения центра тяжести костей.

В этом случае Fcp1=8,35 (Рис.14).

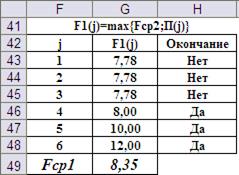
Рис. 14. Результат выполнения четвёртого шага при «краплёных» игральных костях.

Таким образом, ожидаемый выигрыш при оптимальной стратегии меньше, чем сделанная ставка! Принимать условия игры не следует.

Проделанные расчёты можно подкрепить статистическими испытаниями. На Рис.15 показана структура статистической таблицы и результат однократного моделирования при «краплёных» игральных костях.

Рис. 15. Структура таблицы статистических испытаний и результат моделирования при «краплёных» игральных костях.

Таблица для моделирования бросков «краплёных» игральных костей показана на Рис.16. Идеология её построения излагалась в предыдущей лабораторной работе.

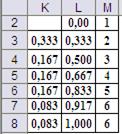
Рис. 16. Таблица для моделирования бросков «краплёных» игральных костей.

Формулы для реализации метода статистических испытаний показаны на Рис.17.

Рис. 17. Ввод формул для реализации метода статистических испытаний.

На Рис.17 показаны формулы только для первого бросания игральной кости. Формулы, моделирующие бросания на следующих шагах, идентичны. Поэтому соответствующие столбцы скрыты.