Проектный анализ
Пример. Фирма «Гигант» разрабатывает инвестиционный проект производства банковских сейфов нового поколения. Инвестиции в данный проект намечено производить в три этапа.
1-ый этап. В начальный момент времени необходимо затратить $500 тыс. на проведение маркетингового исследования рынка.
2-ой этап. Если в результате проведённого исследования обнаружено, что потенциал рынка достаточно высок, то в следующий момент времени фирма «Гигант» инвестирует дополнительно $1000 тыс. на разработку и создание опытных образцов сейфов, подлежащих экспертизе в Специальном центре по безопасности банков, специалисты которого решают вопрос о размещении заказа в данной фирме.
3-ий этап. Если экспертная комиссия вынесла положительное решение о представленных сейфах, то фирма начинает строительство нового предприятия и организацию серийного производства сейфов, для чего ей потребуется ещё $10000 тыс. Реализация данной стадии, по оценкам аналитиков и менеджеров проекта, обеспечит возможность генерирования проектом притоков наличности в течение четырёх лет. Величина притоков зависит от того. Насколько хорошо сейф принят на рынке.
Для анализа и оценки риска рассматриваемого многостадийного процесса целесообразно использовать метод дерева решений (Рис.1)..
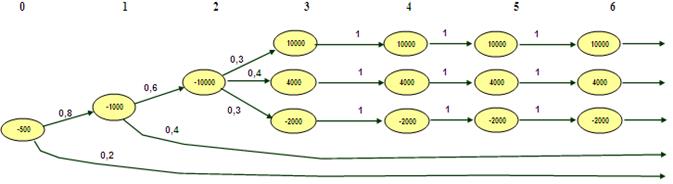
Рис.1. Дерево решения для проекта производства сейфов.
Исходим из предположения, что очередное решение об инвестировании принимается фирмой в конце года. Каждое «разветвление» означает точку принятия решения, либо очередной этап. Число, записанное внутри вершины графа, означает размер инвестиций или размер притока наличностей. Очевидно, что инвестиции записываются отрицательными числами, а притоки наличностей – положительными. Числа на дугах дерева означают вероятности переходов в различные состояния. Так, если фирма «Гигант» решает реализовывать проект в момент времени t=0, то она должна потратить $500 тыс. на проведение маркетингового исследования. По оценкам менеджеров компании, вероятность благоприятного результата равна 0,8, а вероятность получения неблагоприятного результата – 0,2. На дереве решений это отображается самой левой вершиной и двумя дугами, выходящих из неё (момент времени t=0).
Если по результатам маркетингового исследования руководство фирмы приходит к оптимистическому заключению о потенциале рынка, то в момент времени t=1 необходимо потратить ещё $1000 тыс. на изготовление экспериментального образца сейфа. Менеджеры фирмы оценивают вероятность положительного исхода в 0,6, а вероятность отрицательного исхода – 0,4 (вершина с размером инвестиций -1000 и дуги 0,6 и 0,4 в момент времени t=1 на дереве решений).
В случае, если экспертный совет находит данную модель сейфа привлекательной, фирма в момент времени t=2 должна израсходовать ещё $10000 тыс. на строительство нового предприятия и организации серийного производства сейфов. Если фирма «Гигант» приступает к производству сейфов, то операционные потоки наличности в течение четырёхлетнего срока жизни проекта зависят от того, насколько хорошо продукт будет «принят» рынком. По оценкам маркетологов, вероятность того, что рынок положительно воспримет продукт, составляет 0,3, и в этом случае чистые притоки наличности должны составлять около $10000 тыс. ежегодно. Вероятности того, что притоки наличности будут составлять около $4000 тыс. и -$2000 тыс. в год, равны 0,4 и 0,3 соответственно. Эти ожидаемые потоки наличности на дереве решений показаны с третьего года по шестой.
Вероятность реализации пути от начальной вершины до выхода равна произведению вероятностей дуг на этом пути.
В предположении, что средняя учётная банковская ставка составляет 11,5%, рассчитаем чистый дисконтированный доход ( 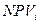 ) по каждому из вариантов, представленных деревом решений
) по каждому из вариантов, представленных деревом решений
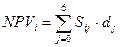 ,
,
где: 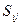 - величина инвестиции (притока наличности) при i-ом варианте решения на j-ом году проекта;
- величина инвестиции (притока наличности) при i-ом варианте решения на j-ом году проекта;
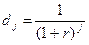 - дисконтирующий множитель для j-ого года;
- дисконтирующий множитель для j-ого года;
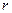 - учётная банковская ставка.
- учётная банковская ставка.
Затем, умножая значения чистого дисконтированного дохода 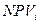 на соответствующее значение вероятности
на соответствующее значение вероятности 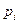 , получаем ожидаемый чистый дисконтированный доход инвестиционного проекта.
, получаем ожидаемый чистый дисконтированный доход инвестиционного проекта.
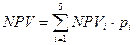 ,
,
Расчёты по изложенной методике реализованы в приложении MS Excel (Рис.2). Ввод формул в ячейки рабочего листа не показан в силу их простоты.
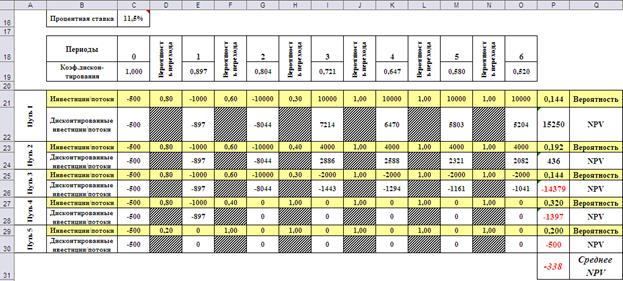
Рис.2. Результаты расчётов для проекта производства сейфов.
Поскольку значение ожидаемого чистого дисконтированного дохода проекта производства сейфов оказалось отрицательным (NPV=-$338 тыс.), то можно предположить, что фирма «Гигант» должна отторгнуть этот инвестиционный проект.
Так как результат зависит от величины учётной банковской ставки, имеет смысл поставить вопрос о нахождении величины банковской ставки, при которой ожидаемый чистый дисконтированный доход проекта будет равен нулю. Это будут граничная учётная ставка: если реальная ставка будет меньше, проект следует принять, а если больше – отвергнуть. Расчёт граничной учётной ставки можно провести с помощью средства «Поиск решений». На Рис.3 показаны установка опций и результаты расчёта.
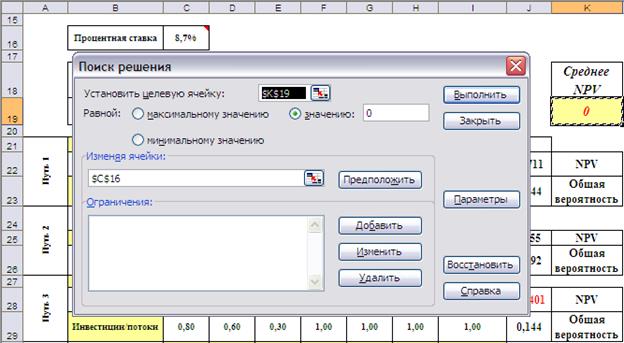
Рис.3. Расчёт граничной учётной ставки.
Итак, граничная учётная ставка равна 8,7%.
Данная задача может быть успешно решена методом статистических испытаний. Для этого необходимо осуществить формализованное описание структуры дерева и его количественных характеристик. Возможный вариант этого заключается в следующем.
Каждой вершине дерева ставится в соответствие таблица вида
| Год/Путь | Инвестиция/Поток | Смещение по строкам | Смещение по столбцам | ||
| p1 | 0+ p1 | Смещение по строкам | Смещение по столбцам | ||
| p2 | 0+ p1+ p2 | Смещение по строкам | Смещение по столбцам | ||
| … | … | … | … | … | |
| pn-1 | n | Смещение по строкам | Смещение по столбцам | ||
| pn | p1+ p2+…+ pn | n | Смещение по строкам | Смещение по столбцам |
Каждая таблица имеет номер в виде «Год/Путь». Формально он не используется, но удобен для описания связей между вершинами. Информационная часть таблицы содержит данные о размере инвестиции или денежном потоке, вероятностях возможных решений, номеров решений и адресов последующих вершин, а точнее таблиц, соответствующих последующим вершинам. Адреса представлены относительными смещениями по строкам и столбцам. Для удобства заполнения таблиц их рационально расположить в соответствии со структурой дерева (Рис.4).
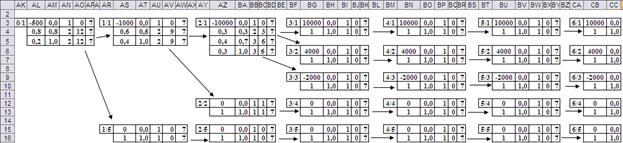
Рис.4. Расположение таблиц вершин дерева.
На нулевом году проекта моделируется принятие одного из двух возможных решений. На последующих годах моделируется одно возможных в соответствии с данными текущей вершины. При этом на каждом году идёт накопление суммы инвестиций или потоков с учётом дисконтирующих коэффициентов. Моделирование возможного пути осуществляется многократно, например 500, результаты (накопленная сумма) усредняются, а затем статистически обрабатываются, как это требует алгоритм метода статистических испытаний. На Рис.5 показана структура таблицы статистических испытаний, а на Рис.6 – ввод формул в таблицу. Часть строк и столбцов скрыта.
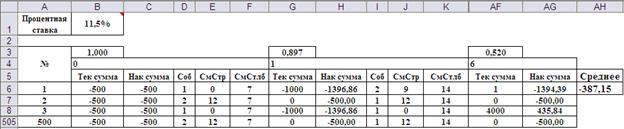
Рис.5. Структура таблицы статистических испытаний.

Рис.6. Ввод формул в таблицу статистических испытаний.
Результаты статистического моделирования соответствуют результатам детерминированного расчёта. Реализация статистического моделирования в данном случае, возможно, покажется более сложной, чем детерминированные расчёты. Однако имеет смысл его осуществить. Приобретённый опыт будет весьма полезен при решении задач, где имеют место вероятностные переходы из одних состояний в другие, например, в системах массового обслуживания.
Дата добавления: 2015-02-19; просмотров: 1466;
