Теоретические основы и рекомендации по выполнению работы

С помощью моделей линейной оптимизации решаются задачи составления оптимальных планах производства, продаж, закупок, перевозок, об оптимальном финансовом планировании, оптимальной организации рекламной кампании и др.

При постановке любой задачи оптимизации необходимо, прежде всего, определить количественную характеристику достигаемой цели – целевую функцию. Это может быть максимум прибыли или минимум издержек (в денежном, временном или каком-либо другом выражении). Целевая функция показывает, почему одно рассматриваемое решение лучше или хуже другого.

Целевая функция зависит от величин, называемых переменными решения. Цель оптимизации найти такие значения переменных решения, при которых целевая функция максимальна или минимальна. Любая оптимизация всегда проводится при наличии некоторых ограничений – условий, ограничивающих изменения переменных решения при поиске максимальной или минимальной целевой функции. Эти ограничения могут диктоваться:

· ограниченностью ресурсов (денежных, временных, материальных);

· установленными «правилами игры» (рыночные ограничения, нормативные акты, лимитирующие ту или иную характеристику или любые требования субъекта, принимающего решения).

Линейное оптимизация имеет дело с моделями, в которых целевая функция 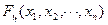линейно зависит от переменных решения 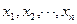и ограничения представляют собой линейные уравнения или неравенства относительно переменных решения.

Фактически, это означает, что целевая функция и ограничения могут представлять собой только суммы произведений постоянных коэффициентов на переменные решения в первой степени, т.е. выражения типа

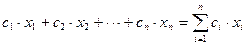
Задачи линейной оптимизации могут быть решены, и реально многие годы решались, симплекс-методом. Однако, с точки зрения быстрейшего достижения цели, рационально использовать возможности современных компьютерных приложений, в частности, надстройку «Поиск решения» (в английском варианте – Solver) приложения MS Excel.

Все задачи в данном сборнике лабораторных работ будут решены именно с помощью этой надстройки. Это, однако, не должно удерживать читателя от использования других средств.