Общая формулировка второго закона термодинамики.

Из первого закона термодинамики следует, что взаимное превращение тепловой и механической энергии в двигателе должно осуществляться в строго эквивалентных количествах. Двигатель, который позволял бы получать работу без энергетических затрат, называется вечным двигателем первого рода. Ясно, что такой двигатель не возможен, ибо он противоречит первому закону термодинамики. Поэтому первый закон можно сформулировать в виде следующего утверждения: вечный двигателя первого рода невозможен.

В 1755 г. французская Академия наук «раз и навсегда» объявила, что не будет больше принимать на рассмотрение какие-либо проекты вечных двигателей.

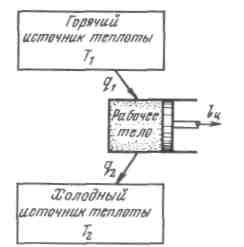
Рис. 7.1 - Термодинамическая схема теплового двигателя

Несмотря на эквивалентность теплоты и работы, процессы их взаимного пре­вращения неравнозначны. Опыт показывает, что механическая энергия может быть полностью превращена в теплоту, например, путем трения, однако теплоту полностью превратить в механическую энергию в периодически повторяющемся процессе нельзя. Многолетние попытки осуществить такой процесс не увенчались успехом. Это связано с существованием фундаментального закона природы, называемого вторым законом термодинамики. Чтобы выяснить его сущность, обратимся к принципиальной схеме теплового двигателя.

Как показал опыт, все без исключения тепловые двигатели должны иметь горячий источник теплоты, рабочее тело, совершающее замкнутый процесс — цикл, и холодный источник теплоты.

Практически в существующих тепловых двигателях горячими источниками служат химические реакции сжигания топлива или внутриядерные реакции, а в качестве холодного источника используется окружающая среда — атмосфера. В качестве рабочих тел, как отмечалось выше, применяются газы или пары.

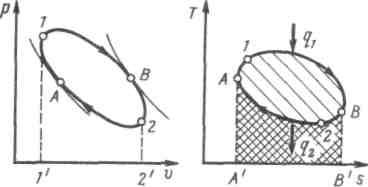
Рис. 7.2 - Круговой процесс (цикл) в р, v и Т, s-координатах

Работа двигателя осуществляется следующим образом. Расширяясь по линии 1B2 , рабочее тело со­вершает работу, равную площади 1B22´1´. В непрерывно действующей тепловой машине этот процесс должен повторяться многократно. Для этого нужно уметь возвращать рабочее тело в исходное состояние. Такой переход можно осуществить в процессе 2В1, но при этом потребуется совершить над рабочим телом ту же самую работу. Ясно, что это не имеет смысла, так как суммарная работа — работа цикла — окажется равной нулю.

Для того чтобы двигатель непрерывно производил механическую энергию, работа расширения должна быть больше работы сжатия. Поэтому кривая сжатия 2A1 должна лежать ниже кривой расширения. Затраченная в процессе 2A1 работа изображается площадью 2A11´2´. В результате каждый килограмм рабочего тела совершает за цикл полезную работу l_ц, эквивалентную площади 1В2А1, ограниченной контуром цикла. Цикл можно разбить на два участка: A1B, на котором происходит подвод теплоты q_1, и B2A, на котором происходит отвод теплоты q₂.В точках А и В нет ни подвода, ни отвода теплоты, и в этих точках поток теплоты меняет знак. Таким образом, для непрерывной работы двигателя необходим циклический процесс, в котором к рабочему телу от горячего источника подводится теплота q₁и отводится от него к холодному теплота q₂. B T,s-диаграмме теплота q₁эквивалентна площади A´A1BB´,a q2 — площади A´A2BB´.

Применим первый закон термодинамики к циклу, который совершает 1 кг рабочего тела:

.

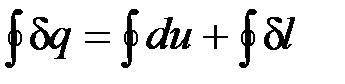Здесь означает интегрирование по замкнутому контуру 1В2А1.

Внутренняя энергия системы является функцией состояния. При возвращении рабочего тела в исходное состояние она также приобретает исходное значение. Поэтому 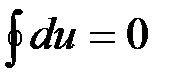, и предыдущее вы­ражение превращается в равенство

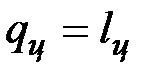, (7.1)

где 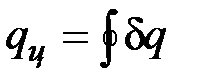представляет собой ту часть теплоты горячего источника, которая превращена в работу. Это — теплота, полезно использованная в цикле, она равна разности теплот и эквивалентна площади, ограниченной контуром цикла в T,s-диаграмме.

Отношение работы, производимой двигателем за цикл, к количеству тепло­ты, подведенной за этот цикл от горячего источника, называется термическим коэффициентом полезного действия (КПД) цикла:

.

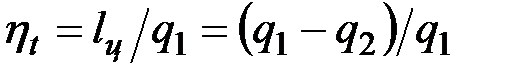Коэффициент полезного действия оценивает степень совершенства цикла теплового двигателя. Чем больше КПД, тем большая часть подведенной теплоты превращается в работу.

Соотношение (7.1) является математическим выражением принципа эквива­лентности тепловой и механической энергии.

Отметим, что если исключить из схемы теплового двигателя холодный источ­ник, то формально принцип эквивалентности не будет нарушен. Однако, как показывает опыт и как следует из проведенного выше анализа работы двигателя, такой двигатель работать не будет.

Тепловой двигатель без холодного источника теплоты, т. е. двигатель, пол­ностью превращающий в работу всю полученную от горячего источника теплоту, называется вечным двигателем второго рода.

Таким образом, второй закон термодинамики можно сформулировать в виде следующего утверждения: «Вечный двигатель второго рода невозможен». В более расшифрованном виде эту формулировку в 1851 г. дал В. Томсон: «Невозможна периодически действующая тепловая машина, единственным результатом действия которой было бы получение работы за счет отнятия теплоты от некоторого источника».

Проблема создания вечного двигателя привлекала исследователей на протяжении длительного времени. Человечество овладело бы неисчерпаемыми запасами внутренней энергии тел, будь построен вечный двигатель второго рода. Действительно, количество теплоты, выделяющейся при охлаждении, например, земного шара всего на 1 К (масса земно­го шара равна кг, его удельную теплоемкость примем равной 840 Дж/(кг-К), равно 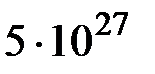Дж. Для сравнения следует указать, что в 2000 г. мировое потребление всех энергоресурсов мира не превысит 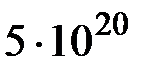Дж, т. е. будет в 10 миллионов раз меньше.

Прямой цикл Карно

Итак, для превращения теплоты в работу в непрерывно действующей машине нужно иметь, по крайней мере, тело или систему тел, от которых можно было бы получить теплоту (горячий источник); рабочее тело, совершающее термо­динамический процесс, и тело, или систему тел, способную охлаждать рабочее тело, т. е. забирать от него теплоту, не превращенную в работу (холодный источник).

Рассмотрим простейший случай, когда имеется один горячий с температурой T₁ и один холодный с температурой T₂ источники теплоты. Теплоемкость каждого из них столь велика, что отъем рабочим телом теплоты от одного источ­ика и передача ее другому практически не меняет их температуры. Хорошей иллюстрацией могут служить земные недра в качестве горячего источника и атмосфера в качестве холодного.

Единственная возможность осуществления в этих условиях цикла, состоящего только из равновесных процессов, заключается в следующем. Теплоту от горячего источника к рабочему телу нужно подводить изотермически. В любом другом случае температура рабочего тела будет меньше температуры источника T₁, т. е. теплообмен между ними будет неравновесным. Равновесно охладить рабочее тело от температуры горячего до температуры холодного источника T₂, не отдавая теплоту другим телам (которых по условию нет), можно только путем адиабатного расширения с совершением работы. По тем же соображениям процесс теплоотдачи от рабочего тела к холодному источнику тоже должен быть изотермическим, а процесс повышения температуры рабочего тела от T₁ до T₂ — адиабатным сжатием с затратой работы. Такой цикл, состоящий из двух изотерм и двух адиабат, носит название цикла К а р н о, поскольку именно с его по­мощью С. Карно в 1824 г. установил основные законы превращения тепловой энергии в механическую.

Осуществление цикла Карно в тепловой машине можно представить следую­щим образом. Газ (рабочее тело) с начальными параметрами, характеризую­щимися точкой а, помещен в цилиндр под поршень, причем боковые стенки цилиндра и поршень абсолютно нетеплопроводны, так что теплота может передаваться, только через основание цилиндра.

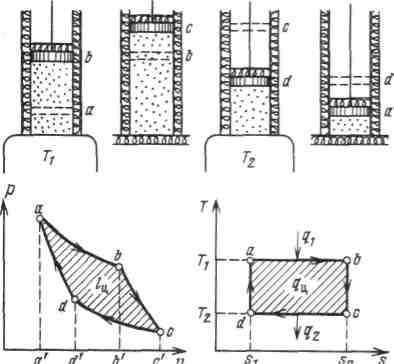
Рис. 7.3 - Прямой цикл Карно

Вводим цилиндр в соприкосновение с горячим источником теплоты. Расширя­ясь изотермически при температуре от объема v_a до объема v_b, газ забирает от горючего источника теплоту 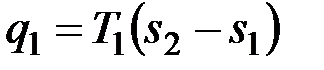. В точке b подвод теплоты прекра­щаем и ставим цилиндр на теплоизолятор. Дальнейшее расширение рабочего тела происходит адиабатно. Работа расширения совершается при этом только за счет внутренней энергии, в результате чего температура газа падает до T₂.

Теперь возвратим тело в начальное состояние. Для этого сначала поместим цилиндр на холодный источник с температурой T₂ и будем сжимать рабочее тело по изотерме cd, совершая работу l₂ и отводя при этом к нижнему источнику от рабочего тела теплоту 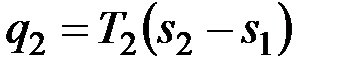. Затем снова поставим цилиндр на теплоизолятор и дальнейшее сжатие проведем в адиабатных условиях. Работа, затраченная на сжатие по линии da, идет на увеличение внутренней энергии, в результате чего температура газа уве­личивается до T₁.

Таким образом, в результате цикла каждый килограмм газа получает от го­рячего источника теплоту q₁, отдает холодному теплоту q₂ и совершает работу l_ц.

Подставив в формулу 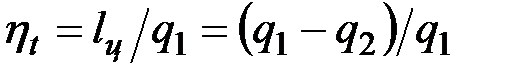, справедливую для любого цикла, выражения для q₁ и q₂, получим, что термический КПД цикла Карно определяется формулой

.

Из нее видно, что термический КПД цикла Карно зависит только от абсолют­ных температур горячего и холодного источников. Увеличить КПД цикла можно либо за счет увеличения температуры горячего источника, либо за счет уменьшения температуры холодного, причем влияние температур и на значение различно:

,

,

а так как .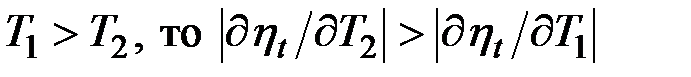

Таким образом, увеличение температуры горячего источника в меньшей сте­пени повышает КПД цикла Карно, чем такое же (в Кельвинах) уменьшение тем­пературы холодного.

Являясь следствием второго закона термодинамики, формула для КПД цикла Карно, естественно, отражает его содержание. Из нее видно, что теплоту горячего источника можно было бы полностью превратить в работу, т. е. получить КПД цикла, равный единице, лишь в случае, когда либо . Оба значения температур недостижимы. (Недостижимость абсолютного нуля температур следует из третьего начала термодинамики).

При T₁=T₂ термический КПД цикла равен нулю.

Это указывает на невозможность превращения теплоты в работу, если все тела системы имеют одинаковую температуру, т. е. находятся между собой в тепловом равновесии. Для ориентировки приводим значения термического КПД цикла Карно при различных температурах горячего источника и при температуре холодного источ­ника, равной 10 °С.

Таблица №7.1.

t,°С
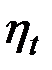
	0,40	0,58	0,68	0,74	0,78	0,81	0,83	0,85

Приведенные цифры дают КПД иде­ального цикла. Коэффициент полезного действия реального теплового двигателя, конечно, ниже.