Энтропия.

Как уже указывалось, величина 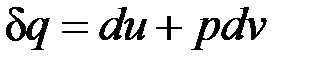не является полным диффе­ренциалом. Действительно, для того чтобы проинтегрировать правую часть этого выражения, нужно знать зависимость р от v, т. е. процесс, который совершает газ.

В математике доказывается, что дифференциальный двучлен всегда можно превратить в полный дифференциал путем умножения (или деления) на интег­рирующий множитель (или делитель). Таким интегрирующим делителем для элементарного количества теплоты q является абсолютная температура Т.

Покажем это на примере изменения параметров идеального газа в равновес­ных процессах:

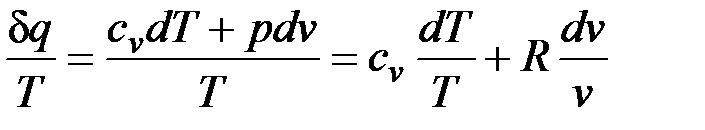, (4.3)

Выражение 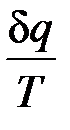при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния. Она называется энтропией, обозначается для 1 кг газа через s и измеряется в Дж/(кгК). Для произвольного количества газа энтропия, обозначаемая через S, равна S=Ms и измеряется в Дж/К.

Таким образом, аналитически энтропия определяется следующим образом:

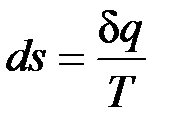, (4.4)

Формула (4.4) справедлива как для идеальных газов, так и для реальных тел. Подобно любой другой функции состояния энтропия может быть представлена в виде функции любых двух параметров состояния:

; ; .

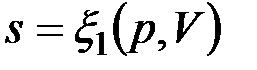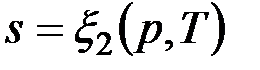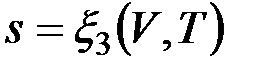Значение энтропии для заданного состояния определяется интегрированием уравнения (4.4):

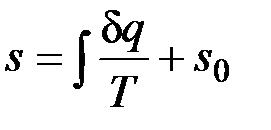
где 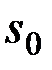— константа интегрирования.

При температурах, близких к абсолютному нулю, все известные вещества находятся в конденсированном состоянии. В. Нернст (1906 г.) экспериментально установил, а М. Планк (1912 г.) окончательно сформулировал следующий принцип: при температуре, стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю, т. е. s₀ = 0 при Т = 0 К. Этот закон называют третьим законом термодинамики или тепловой теоремой Нернста. Он позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии, которые всегда отсчитываются от произвольного уровня.

Однако в технической термодинамике обычно используется не абсолютное значение энтропии, а ее изменение в каком-либо процессе:

,

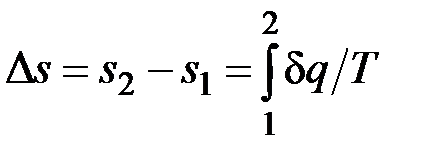поэтому энтропию тоже часто отсчитыва­ют от произвольно выбранного уровня.

Получим формулы, позволяющие вычислить изменение энтропии идеального газа. Для этого проинтегрируем уравнение (4.3), положив для простоты cv= const:

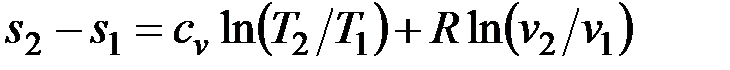, (4.5)

Из уравнения Клапейрона, записанного для состояний 1 и 2, следует:

.

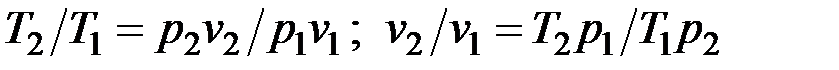После подстановки отношений и в выражение (4.4) получим следующие формулы для изменения энтропии идеального газа:

;

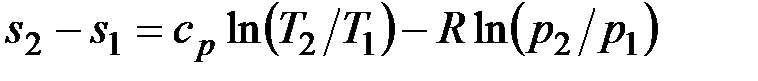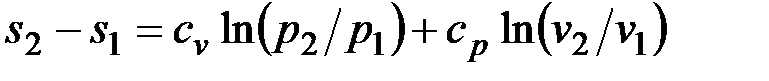, (4.6)

Поскольку энтропия есть функция состояния рабочего тела, уравнениями (4.5) — (4.6) можно пользоваться вне зависимости от пути перехода рабочего тела между состояниями 1 и 2 и, в частности, от того, равновесный этот переход или нет.

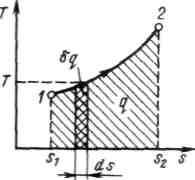
Рис. 4.2 - Графическое изображение теплоты в T, s – координатах

Понятие энтропии позволяет ввести чрезвычайно удобную для термодинами­ческих расчетов Т, s-диаграмму, на которой (как и на p,v -диаграмме) состояние термодинамической системы изображается точкой, а равновесный термодина­мический процесс линией (Рисунок 4.2).

В равновесном процессе

;

.

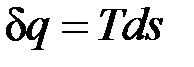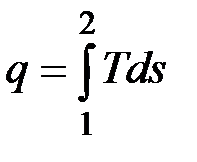Очевидно, что в Т, s-диаграмме элементарная теплота процесса 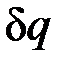изобра­жается элементарной площадкой с высо­той Т и основанием ds, а площадь, огра­ниченная линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.

Формула 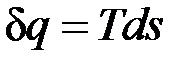показывает, что ds и 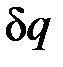имеют одинаковые знаки, следова­тельно, по характеру изменения энтропии в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты к телу ( 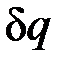>0) его энтропия возрастает (ds>0), а при отводе теплоты ( 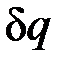<0) — убывает (ds<0).