Эксергия

Основываясь на втором начале термодинамики, установим количественное соотношение между работой, которая могла бы быть совершена системой при данных внешних условиях в случае протекания в ней равновесных процессов, и действительной работой, производимой в тех же условиях, при неравновесных процессах.

Рассмотрим изолированную систему, состоящую из горячего источника с тем­пературой Ti, холодного источника (окружающей среды) с температурой То и рабочего тела, совершающего цикл.

Работоспособностью (или эксергией) теплоты Q₁, отбираемой от горячего источника с температурой Т₁, называется максимальная полезная работа, которая может быть получена за счет этой теплоты при условии, что холодным источником является окружающая среда с температурой Т₀.

Из предыдущего ясно, что максимальная полезная работа L'_макс теплоты Q₁ представляет собой работу равновесного цикла Карно, осуществляемого в диапазоне температур T₁ –T₀.

,

где

Таким образом, эксергия теплоты Q₁

,

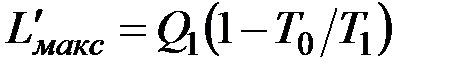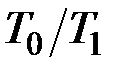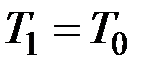т. е. работоспособность теплоты тем больше, чем меньше отношение . При она равна нулю.

Полезную работу, полученную за счет теплоты Q₁ горячего источника, можно представить в виде , где — теплота, отдаваемая в цикле холодному источнику (окружающей среде) с температурой .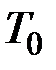

Если через 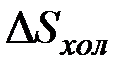обозначить приращение энтропии холодного источника, то ,

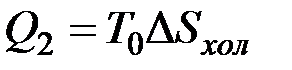тогда

, (5.3)

Если бы в рассматриваемой изолированной системе протекали только равно­весные процессы, то энтропия системы оставалась бы неизменной, а увеличение энтропии холодного источника равнялось бы уменьшению энтропии горячего. В этом случае за счет теплоты Q₁ можно было бы получить максимальную полезную работу

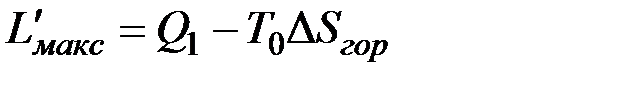
что следует из уравнения (5.3).

Действительное количество работы, произведенной в этих же условиях, но при неравновесных процессах, определяется уравнением (5.3).

Таким образом, потерю работоспособности теплоты можно записать как 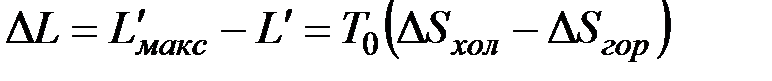, но разность 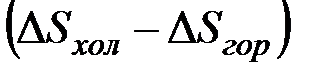представляет собой изменение энтропии рассматриваемой изолированной системы, поэтому

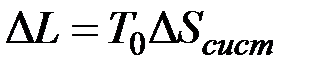, (5.4)

Величина определяет потерю работы, обусловленную рассеиванием энергии вследствие неравновесности протекающих в системе процессов. Чем больше неравновесность процессов, мерой которой является увеличение энтропии изолированной системы , тем меньше производимая системой работа.

Уравнение (5.4) называют уравнением Гюи — Стодолы по имени французского физика М. Гюи, получившего это уравнение в 1889 г., и словацкого теплотехника А. Стодолы, впервые применившего это уравнение.