Передача значений функций

Основным способом обмена информацией между вызываемой и вызывающей функциями являются механизм параметров. Существует два способа передачи параметров в функцию: по адресу и по значению.

При передаче по значению выполняются следующие действия:

● вычисляются значения выражений, стоящие на месте фактических параметров;

● в стеке выделяется память под формальные параметры функции;

● каждому фактическому параметру присваивается значение формального параметра, при этом проверяются соответствия типов и при необходимости выполняются их преобразования.

Например:

double square(double a, double b, double c) {

/*функция возвращает площадь треугольника, заданного длинами сторон а,b,c*/

double s, p=(a+b+c)/2;

return s=sqrt(p*(p-a)*(p-b)*(p-c));//формула Герона

}

1) double s1=square(2.5,2,1);

2) double a=2.5,b=2,c=1;

double s2=square(a,b,c);

3) double x1=1,y1=1,x2=3,y2=2,x3=3,y3=1;

double s3=square(

sqrt(pow(x1-x2,2)+pow(y1-y2,2)),//расстояние между 1 и 2

sqrt(pow(x1-x3,2)+pow(y1-y3,2)),//расстояние между 1 и 3

sqrt(pow(x3-x2,2)+pow(y3-y2,2)));//расстояние между 2 и3

Таким образом, в память заносятся копии фактических параметров, и операторы функции работают с этими копиями. Доступа к самим фактическим параметрам у функции нет, следовательно, нет возможности их изменить.

При передаче по адресу в память заносятся копии адресов параметров, следовательно, у функции появляется доступ к ячейке памяти, в которой находится фактический параметр и она может его изменить.

Например:

void Change(int a,int b) { //передача по значению

int r=a; a=b; b=r;

}

int x=1,y=5;

Change(x,y);

cout << ”x=” << x << ”y=” << y;

выведется: x=1 y=5

void Change(int *a,int *b) { //передача по адресу

int r=*a; *a=*b; *b=r;

}

int x=1,y=5;

Change(&x,&y);

cout << ”x=” << x << ”y=” << y;

выведется: x=5 y=1

Для передачи по адресу также могут использоваться ссылки. При передаче по ссылке в функцию передается адрес указанного при вызове параметра, а внутри функции все обращения к параметру неявно разыменовываются.

void Change(int &a,int &b){

int r=a; a=b; b=r;

}

int x=1,y=5;

Change(x,y);

cout << ”x=” << x << ”y=” << y;

выведется: x=5 y=1

Использование ссылок вместо указателей улучшает читаемость программы, т.к. не надо применять операцию разыменовывания. Использование ссылок вместо передачи по значению также более эффективно, т.к. не требует копирования параметров. Если требуется запретить изменение параметра внутри функции, используется модификатор const. Рекомендуется ставить const перед всеми параметрами, изменение которых в функции не предусмотрено (по заголовку будет понятно, какие параметры в ней будут изменяться, а какие нет).

Пример 1. Для данных трех натуральных чисел найдите их НОД. Разработайте функцию нахождения НОД двух чисел.

#include <stdio.h>

long NOD (long x,long y);

void main (){

long a,b,c,z;

printf("Введите первое число = ");

scanf("%ld",&a);

printf("Введите второе число = ");

scanf("%ld",&b);

printf("Введите третье число = ");

scanf("%ld",&c);

z=NOD(c,NOD(a,b));

printf("Наибольший общий делитель 3 чисел равен %ld",z);

}

long NOD(long x,long y){

long x1,y1;

while (y!=0){

x1=y;

y1=x%y;

x=x1;

y=y1;

}

return x;

}

Задания

Для решения задач используйте метод процедурной абстракции

1.Дано натуральное число n. Найти все меньшие n числа Мерсена. Простое число называется числом Мерсена, если оно может быть представлено в виде 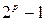где p – тоже простое число. Например, 31=2⁵–1 – число Мерсена.

2.Для данных k натуральных чисел найдите их НОД. Разработайте функцию нахождения НОД двух чисел.

3.Два простых числа называются «близнецами», если они отличаются друг от друга на 2 (например, 41 и 43). Напечатать все пары «близнецов» из отрезка [n, 2n], где n – заданное натуральное число, большее 2.

4.Вычислите результат выражения 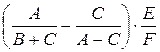в виде обыкновенной дроби, где A, B, C, E, F – целые числа. Разработайте функции сложения и умножения двух дробей, а также функцию сокращения дроби.

Домашние задания

1.Для данного натурального N найдите сумму факториалов: 1! + 2! + 3! + … + N!

2.Имеется кусок льда массой Мl при температуре 0^оС, который нагревается за счет сжигания каменного угля массой Mu (потерями энергии пренебречь). Определите агрегатное состояние нагреваемого вещества после полного сгорания угля. Физические величины следует взять из справочника и оформить как константы.

3. Индивидуальное задание. Номер варианта определяется по журналу. Составьте программу для решения задачи.

Варианты индивидуального задания

№	Задание
1.	Даны основания и высоты двух равнобедренных трапеций. Найти сумму их периметров. Определите функцию для расчета периметра равнобедренной трапеции по ее основаниям и высоте.
2.	Найдите сумму первых n чисел последовательности Фибоначчи. Разработайте функцию нахождения k-го числа последовательности Фибоначчи.
3.	Дана квадратная матрица размерности 3´3. Найдите ее определитель. Разработайте функцию вычисления определителя второго порядка.
4.	Описать функцию DigitN(K, N) целого типа, возвращающую N-ю цифру целого положительного числа K (цифры в числе нумеруются справа налево). Если количество цифр в числе K меньше N, то функция возвращает –1.
5.	Описать функцию Exp1(x, ε) вещественного типа (параметры x, ε – вещественные, ε > 0), находящую приближенное значение функции exp(x): exp(x) = 1 + x + x2/(2!) + x3/(3!) + … + xn/(n!) + … В сумме учитывать все слагаемые, большие ε. С помощью Exp1 найти приближенное значение экспоненты для данного x при заданном ε.
6.	Описать функцию Sin1(x, ε) вещественного типа (параметры x, ε — вещественные, ε > 0), находящую приближенное значение функции sin(x): sin(x) = x – x3/(3!) + x5/(5!) – … + (–1) n·x2n+1/((2n+1)!) + … . В сумме учитывать все слагаемые, модуль которых больше ε. С помощью Sin1 найти приближенное значение синуса для данного x при заданном ε.
7.	Даны вещественные числа x1,y1,x2,y2,…x5,y5. Найти площадь пятиугольника, вершины которого имеют координаты (x1,y1), (x2,y2), …, (x5,y5). Разработайте функции для определения существования пятиугольника и расчета площади треугольника по координатам его вершин.
8.	Описать функцию IsPalindrom(K), возвращающую True, если натуральный параметр K является палиндромом (то есть его запись читается одинаково слева направо и справа налево), и False в противном случае. С ее помощью найти количество палиндромов на заданном отрезке [a,b].
9.	На отрезке с натуральными границами [a,b] найдите все полные квадраты. Определите функцию, позволяющую распознать, является ли данное число полным квадратом. Натуральное число является полным квадратом, если оно является квадратом натурального числа. Например, 36 – полный квадрат, так как 62=36.
10.	Даны два натуральных числа. Выяснить, в каком из них произведение цифр больше. Определите функцию для расчета произведения цифр натурального числа.
11.	Найдите все натуральные трехзначные числа из отрезка [a, b], сумма квадратов цифр которых равна заданному натуральному k. Разработайте функцию подсчета суммы квадратов цифр трехзначного числа.
12.	Описать функцию Cos1(x, ε) вещественного типа (параметры x, ε – вещественные, ε > 0), находящую приближенное значение функции cos(x): cos(x) = 1 – x2/(2!) + x4/(4!) – … + (–1)n x2n/((2·n)!) + … . В сумме учитывать все слагаемые, модуль которых больше ε. С помощью Cos1 найти приближенное значение косинуса для данного x при заданном ε.
13.	На отрезке с натуральными границами [a,b] найдите все степени пятерки. Определите функцию, позволяющую распознать, является ли данное число степенью пятерки.
14.	Два простых числа называются «близнецами», если отличаются дуг от друга на 2 (таковы, например, числа 41 и 43). Напечатать все пары чисел-«близнецов», не превышающих число 200. Определите функцию, позволяющую распознать простые числа.
15.	Даны два натуральных числа. Выяснить, в каком из них сумма цифр больше. Определите функцию для расчета суммы цифр натурального числа.
16.	Найдите сумму двойных факториалов чисел до данного натурального n включительно. Разработайте функцию вычисления двойного факториала натурального числа.
17.	Описать функцию NOD2(A, B) целого типа, находящую наибольший общий делитель (НОД) двух целых положительных чисел A и B, используя алгоритм Евклида: НОД(A, B) = НОД(B, A mod B), если B ≠ 0; НОД(A, 0) = A. С помощью этой функции найти наибольший среди наибольших общих делителей пар (A, B), (A, C), (С, D), если даны числа A, B, C, D.
18.	Описать функцию sign(X) целого типа, возвращающую для вещественного числа X следующие значения: 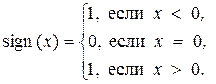С помощью этой функции найти значение выражения (sign (A) + sign (B)) · sign (A–B) для данных вещественных чисел A и B.
19.	Учитывая, что наименьшее общее кратное двух целых положительных чисел A и B равно A · B / НОД(A, B), где НОД(A, B) — наибольший общий делитель A и B, опишите функцию NOK2(A, B) целого типа, находящую наименьшее общее кратное чисел A и B. С помощью NOK2 найти наименьшее среди наименьших общих кратных пар (A, B), (A, C), (В, D), если даны числа A, B, C, D.
20.	Описать функцию IsLeapYear(Y) логического типа, которая возвращает True, если натуральное Y является номером високосного года, и False в противном случае. Вывести все високосные года из временного промежутка [a, b]. Високосным считается год, делящийся на 4, за исключением тех годов, которые делятся на 100 и не делятся на 400.
21.	Разложите заданное натуральное число n на простые множители. Разработайте функцию определения простого числа. Например, для числа 120 ответом должна быть последовательность: 2 2 2 3 5.
22.	Составьте программу вывода на экран и подсчета количества всех натуральных чисел, меньших М, квадрат суммы цифр которых равен X.
23.	Составьте программу вывода на экран и подсчета количества всех натуральных чисел, не превосходящих N и делящихся на каждую из своих цифр.
24.	Напишите программу вычисления суммы квадратов простых чисел, лежащих в интервале (M, N).
25.	Составьте программу вычисления суммы трехзначных чисел, в десятичной записи которых нет четных цифр.
26.	Даны натуральные m и n (m<n). Составить программу, сокращающую дробь m/n.
27.	Определите, в какой сотне больше простых чисел. Рассмотрите сотни со второй до десятой.
28.	В пространстве даны три некомпланарных вектора своими координатами. Найдите площадь поверхности параллелепипеда, построенного на этих векторах. Разработайте функцию вычисления площади параллелограмма, построенного на двух векторах.