Вложенные циклы
Существует возможность организовать цикл внутри тела другого цикла. Такой цикл будет называться вложенным циклом. Вложенный цикл по отношению к циклу, в тело которого он вложен, будет именоваться внутренним циклом. Цикл, в теле которого существует вложенный цикл, будет именоваться внешним циклом по отношению к вложенному. Внутрь вложенного цикла в свою очередь может быть вложен еще один цикл, образуя следующий уровень вложенности и так далее. Количество уровней вложенности, как правило, не ограничивается.
Полное число исполнений тела внутреннего цикла не превышает произведения числа итераций внутреннего и всех внешних циклов. Например, взяв три вложенных друг в друга цикла, каждый по 10 итераций, получим 10 исполнений тела для внешнего цикла, 100 для цикла второго уровня и 1000 в самом внутреннем цикле.
Одна из проблем, связанных с вложенными циклами, – организация досрочного выхода из них. В языке С++ для этого есть оператор досрочного завершения цикла break, но он, как правило, обеспечивает выход только из цикла того уровня, откуда вызван. Вызов его из вложенного цикла приведёт к завершению только этого внутреннего цикла, внешний же цикл продолжит выполняться. Проблема может показаться надуманной, но она действительно иногда возникает при программировании сложной обработки данных, когда алгоритм требует немедленного прерывания в определённых условиях, наличие которых можно проверить только в глубоко вложенном цикле.
Пример 4. Напечатать n простых чисел.
#include<stdio.h>
void main() {
int a=1,n,d,i;
printf("\nВведите n=");
scanf("%d", &n);
for(i=0;i<n;)//внешний цикл
{
a++;d=1;
do //внутренний цикл
{
d++;
}
while(a%d!=0);// конец внутреннего цикла
if(a==d){
printf("a=%d\n", a);
i++;}
}// конец внешнего цикла
}
Задания
1.Составьте программу для решения задачи. Найти наибольший общий делитель двух заданных натуральных чисел, используя алгоритм Евклида.
2.Составьте программу для решения задачи. Напечатайте числа в виде таблицы для данного натурального n. В приведенном примере n=6.
6 5 4 3 2
5 4 3 2
4 3 2
3 2
3.Натуральное число называется совершенным, если оно равно сумме своих делителей, включая 1 и, естественно, исключая самое число. Например, совершенным является число 6 (6= 1+2+3). Найти все совершенные числа, меньшие 10 000.
Домашние задания
1.Наберите коды программ из Примеров 1, 2, 3 и 4. Сохраните коды программ. Выполните компиляцию и запуск программ. Введите свои данные в качестве входных.
2.Составьте программу для решения задачи. Найти наименьшее общее кратное двух заданных натуральных чисел.
3.Составьте программу для решения задачи. Напечатайте полную таблицу умножения в виде:
Таблица умножения.
1*1=1 1*2=2 . . . 1*9=9
2*1=2 2*2=4 . . . 2*9=18
. . . . . . . . . . . . . . . . . .
9*1=9 9*2=18 . . . 9*9=81
4.Составьте программу для решения задачи. Два натуральных числа называются дружественными, если каждое из них равно сумме всех делителей другого (само другое число в качестве делителя не рассматривается). Например, 220 (1+2+4+5+10+11+20+22+44+55+110=284) и 284 (1+2+4+71+142=220) – дружественные числа. Пары необходимо выводить по одной в строке, разделяя пробелами. Найти все пары натуральных дружественных чисел, меньших 10 000.
5. Индивидуальное задание №1. Номер варианта определяется по журналу. Составьте программу для решения задачи. Вычислите сумму для заданного натурального n и вещественного x.
6. Индивидуальное задание №2. Номер варианта определяется по журналу. Составьте программу для решения задачи. Дана последовательность целых чисел, за которой следует 0.
Варианты индивидуального задания №1
| № | Задание |
| 1. | 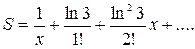
|
| 2. | 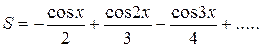
|
| 3. | 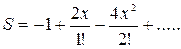
|
| 4. | 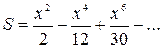
|
| 5. | 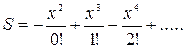
|
| 6. | 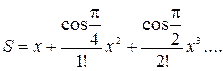
|
| 7. | 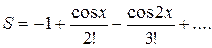
|
| 8. | 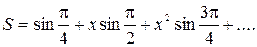
|
| 9. | 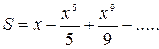
|
| 10. | 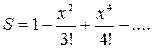
|
| 11. | 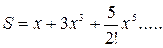
|
| 12. | 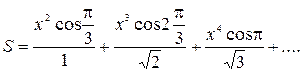
|
| 13. | 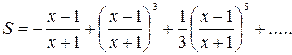
|
| 14. | 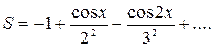
|
| 15. | 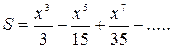
|
| 16. | 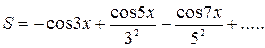
|
| 17. | 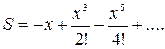
|
| 18. | 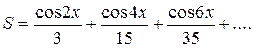
|
| 19. | 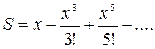
|
| 20. | 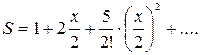
|
| 21. | 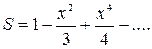
|
| 22. | 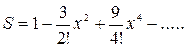
|
| 23. | 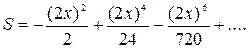
|
| 24. | 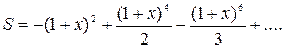
|
| 25. | 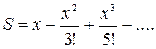
|
| 26. | 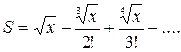
|
| 27. | 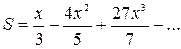
|
| 28. | 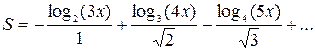
|
Варианты индивидуального задания №2
| № | Задание |
| 1. | Найти сумму четных элементов этой последовательности. |
| 2. | Найти сумму элементов с четными номерами из этой последовательности. |
| 3. | Найти количество элементов, расположенных после первого минимального. |
| 4. | Найти сумму элементов с нечетными номерами из этой последовательности. |
| 5. | Найти количество элементов, расположенных после последнего максимального. |
| 6. | Найти разность минимального и максимального элементов в этой последовательности. |
| 7. | Найти количество элементов, расположенных после последнего минимального. |
| 8. | Найти количество четных элементов этой последовательности. |
| 9. | Найти количество элементов этой последовательности, кратных ее первому элементу. |
| 10. | Найти количество элементов этой последовательности, кратных числу K1 и не кратных числу K2. |
| 11. | Определить, каких чисел в этой последовательности больше: положительных или отрицательных. |
| 12. | Определить, каких чисел в этой последовательности меньше: четных или нечетных. |
| 13. | Найти номер первого минимального элемента этой последовательности. |
| 14. | Найти номер первого максимального элемента этой последовательности. |
| 15. | Найти номер последнего минимального элемента этой последовательности. |
| 16. | Найти номер последнего максимального элемента этой последовательности. |
| 17. | Найти минимальный положительный элемент этой последовательности. |
| 18. | Найти минимальный отрицательный элемент этой последовательности. |
| 19. | Найти максимальный отрицательный элемент этой последовательности. |
| 20. | Найти максимальный положительный элемент этой последовательности. |
| 21. | Найти количество элементов, расположенных перед первым минимальным. |
| 22. | Найти количество элементов, расположенных перед первым максимальным. |
| 23. | Найти сумму минимального и максимального элементов в этой последовательности. |
| 24. | Найти количество нечетных элементов этой последовательности. |
| 25. | Найти количество элементов, расположенных перед последним максимальным. |
| 26. | Найти сумму нечетных элементов этой последовательности. |
| 27. | Найти количество элементов, являющихся совершенными числами. |
| 28. | Найти количество элементов, являющихся простыми числами. |
Дата добавления: 2015-02-16; просмотров: 2527;
