ЧАСТЬ I. ОСНОВЫ МОНТАЖА ОБОРУДОВАНИЯ 2 страница

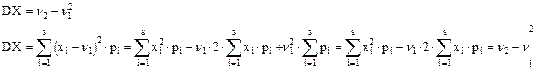
Построим функцию распределения для дискретной случайной величины. Для удобства договоримся, что случайные величины располагаются в порядке возрастания.

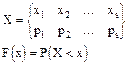
т.е. по определению для любого действительного X, F(x) численно равно вероятности наступления следующего события: в результате испытаний над X оно приняло значение строго меньше x.

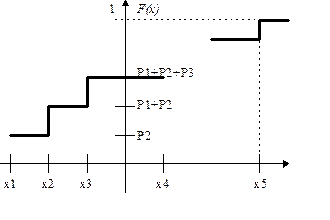
Производная функция

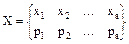
Характеристической функцией случайной величины X называется функция действительного аргумента вида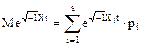

Производящей функцией называется скалярная функция вида:

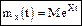
Свойства производящей функции

1.

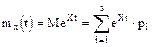
2.

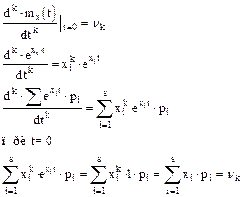
3. Разложение производящей функции в ряд Маклорена имеет вид

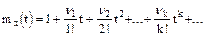
Формула Тейлора имеет вид

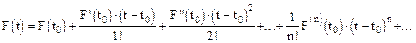
при to=0 она носит название формулы Маклорена

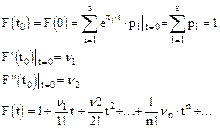
Пример:

Рассмотрим случайную величину, распределенную по биноминальному закону распределения:

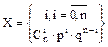
Найдем производящую функцию:

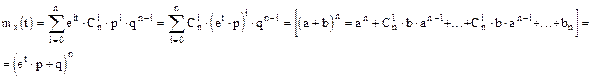
Найти DX и MX

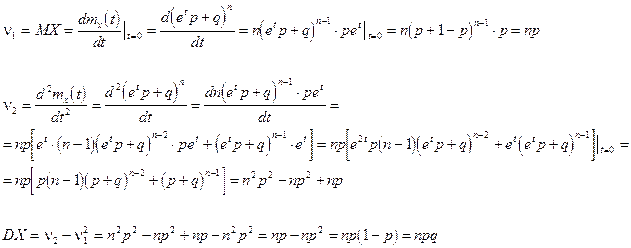
Первая модель распределения Пуассона

Проведена неограниченно большая серия испытаний, в результате каждого испытания случайным образом появляется точка на числовой оси. Случайное распределение точек на числовой оси удовлетворяет следующим трем свойствам.

1. Стационарность. Вероятность того, что на отрезок данной длины попадает данное количество точек определяется только длиной этого отрезка и не зависит от расположения этого отрезка на числовой оси.

2. Ординарность. Вероятность того, что на достаточно малый отрезок длины Dx попадает одна точка, является бесконечно малой Dx порядка. Вероятность того, что на этот отрезок попадает более, чем одна точка, является бесконечно малой более высокого порядка, чем Dx.

3. Свойство без последействия. Вероятность того, что на данный отрезок попало определенное количество точек не зависит от того, сколько точек в результате проведенной бесконечно серии испытаний попало на отрезок, не пересекающийся с данным.

Найти вероятность того, что на данный отрезок длина l попадает m точек.

Обозначим через x^l - случайная величина, равная численности точек, выпавших на отрезок длины l.

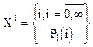
На числовой оси рассмотрим отрезок длины 1 и обозначим:

MX¹=l

Математическое ожидание числа точек, попавших на отрезок длины 1. По свойству стационарности l одинаково для всех отрезков.

MX¹=ll - доказать

Пусть l - целое число. Разобьем отрезок длины l на l отрезков единой длины. Тогда количество точек, попавших на отрезок длины l будет равно числу точек, попавших на каждый из непересекающихся отрезков длины 1 (тут использовалось свойство беспоследействия).

Используя формулу

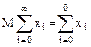
имеем

MX¹=ll

Математическое ожидание числа точек, попавшие на отрезок длины l равно мат. ожиданий точек, попавших на непересекающиеся отрезки. Пусть l - не целое число. Выделяем целую часть. Тогда

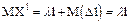
На числовой оси рассмотрим отрезок длины l, разобьем его на n отрезков данной длины

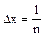
такой, что позволит использовать свойство ординарности. Тогда с определенной погрешностью, которая тем меньше, чем больше n можно считать

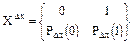
т.е. на отрезок длины Dx попадает не более, чем одна точка, тогда

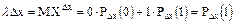
Для достаточного малого отрезка длины lDx вероятность попадания в него одной точки Dx, а вероятность того, что ничего не произойдет 1- lDx.

В сделанных предположениях m точек попадает на отрезок длины l только в одном случае, когда в m отрезках попадает по одной точке. Тогда на основании 3-го свойства искомая вероятность равна

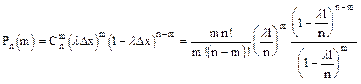
Точную вероятность получим путем предельного перехода при числе разделений отрезка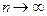

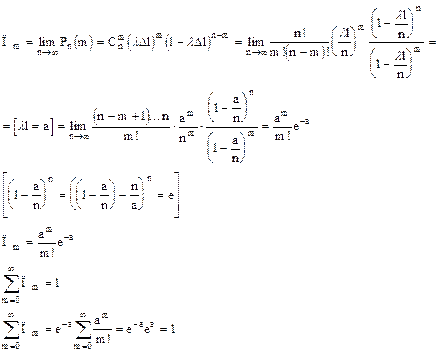
Тут мы разложили 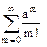в ряд Маклорена.

Найдем производящую функцию распределения Пуассона

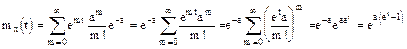
Найти MX и DX

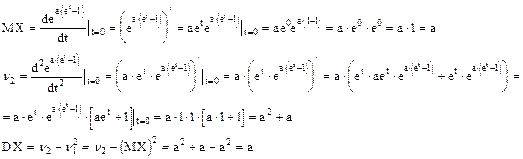
Вторая модель распределения Пуассона

Рассматривается обычная схема биноминального распределения, в котором n - велико, а p - достаточно мало. Тогда точная формула для вероятности появления события A в m испытаниях имеет вид

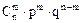
Эта формула при больших n вычисляется сложно. Такую вероятность заменяют приближенной

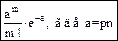
Для найденного a построим гипотетический ряд вероятностей

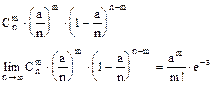
Предполагается, что для достаточно больших n и малых p искомая вероятность

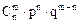
является членом построенного гипотетического ряда вероятностей, а во вторых находится в малой окрестности предельного значения этого ряда. И, следовательно, это значение можно взять в качестве допустимой хорошей аппроксимации значений искомой вероятности.

Непрерывные случайные величины.

Будем рассматривать пространство элементарных событий как совокупность всех точек числовой оси. В этом случае введенная ранее функция распределения имеет вид: .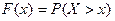

Пусть функция распределения является непрерывной. Найдем вероятность того, что в результате испытаний случайная величина X примет значение a, где a - произвольное действительное число.

P(X=a).

Рассмотрим неравенство:

Доказать самим.

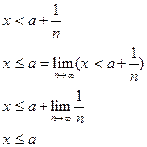
Следовательно:

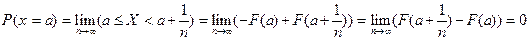
Мы впервые столкнулись с ситуацией, когда событие принципиально может произойти в результате испытания, но имеет вероятность равную 0 . В инженерном толковании это означает: в данной конечной серии испытаний данное событие никогда не произойдет.

Случайная величина X называется непрерывной, если ее пространством элементарных событий является вся числовая ось (либо отрезок (отрезки) числовой оси), а вероятность наступления любого элементарного события равна нулю.

P(a£X<b)=P(a£X£b)=F(b)-F(a)

Если от сложного события вычесть конечное либо счетное множество, вероятность наступления нового события останется неизменной.

Функция f(x) - числовая скалярная функция действительного аргумента x называется плотностью вероятности, и существует в точке x, если в этой точке существует предел:

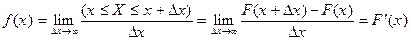
Свойства плотности вероятности.

1. Плотность вероятности является неотрицательной функцией.

2.

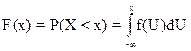
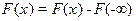
3.

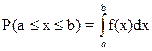
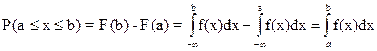
4.

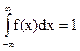
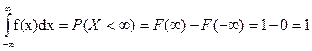
Следствие: Если пространством элементарных событий является отрезок числовой оси, то пространство элементарных событий формально можно распространить на всю числовую ось, положив вне отрезка значение плотности вероятности равное 0.

Второе эквивалентное определение плотности вероятности.

Если плотность вероятности в точке x существует, то P(x£X£x+Dx)=f(x)Dx+о(Dx). Вероятность того, что в результате испытания случайная величина примет значение в отрезке с точностью до о(Dx) равна F(x)Dx.

Пример:

Равномерное распределение.

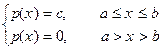тут p(x)=f(x).

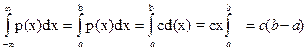
т.к.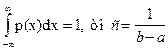

Экспоненциальное распределение.

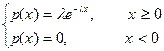
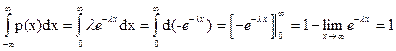
Непрерывная случайная величина является математической абстракцией и в чистом виде на практике не встречается, хотя бы потому, что теоретически не может существовать измерительное устройство, вычисляющее это величину. Следовательно, всегда исследователь имеет дело со случайными дискретными величинами. На практике отрезок [a, b] разбивают на отрезки одинаковой длинны, длину устремляют к нулю. При этом x принадлежит отрезку. Вероятность того, что отрезок содержит x равна 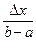. При 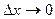ситуация эквивалентна следующему: имеется бесконечное множество лотерейных билетов, один ваш. Ясно, что в конечной серии розыгрышей вы никогда не выиграете. Независимо от этого велико удобство работы с непрерывными величинами. Оно заключается в том, что вероятностные свойства задаются одной из двух функций - плотностью распределения либо плотностью вероятности.

Вероятностные характеристики непрерывных случайных величин.

Пусть имеется случайная величина, являющаяся функцией от непрерывной случайной величины X.

Y=x(x)

Математическим ожиданием непрерывной случайной величены является число:

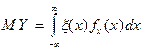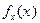, - плотность вероятности случайной величины.

Обоснование этой формулы.

Аппроксимируем непрерывную случайную величину Y случайной величены Y^*, которая является дискретной. Пусть числовая ось - пространство элементарных событий случайной величены X, разобьем всю числовую ось на отрезки достаточно малой длины.

2n отрезков.

Если в результате испытания случайная величена X попала в отрезок с начальной вершиной x_i, то случайная величена X^* приняла значение x(x_i) с точностью до бесконечно малой Dx - длины i-го отрезка. Вероятность того, что Y^* примет значение x(x_i) с точностью до бесконечно малой более высокого порядка, чем Dx, тем более точно Y^* аппроксимирует Y.

Вероятность наступления x(x_i) для Y^* равна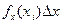

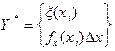
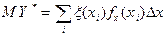, при 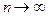эта сумма переходит в .

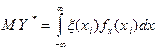Тогда .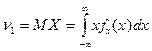

Самим показать, что все свойства мат. ожидания для дискретной случайной величены сохраняются для непрерывной случайной величены.

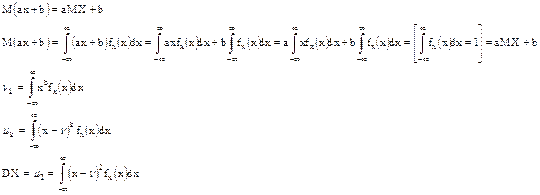
Доказать, что

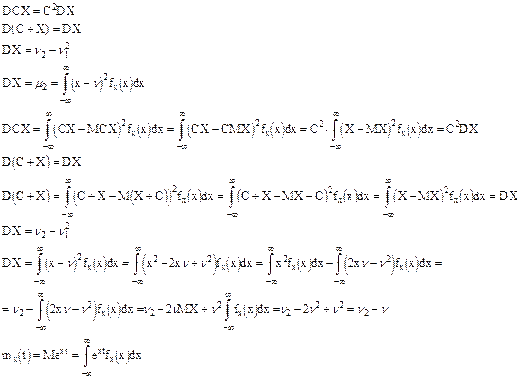
Доказать самим, что свойство 1 и 2 для производящей функции в дискретном случае справедливы и для непрерывного.

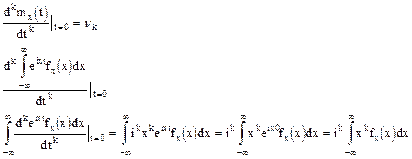
Распределение Гаусса - нормальное

Случайная величина имеет нормальное распределение (распределение Гаусса) и называется нормально распределенной, если ее плотность вероятности

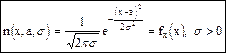
Из определения

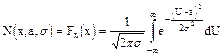
функция распределения

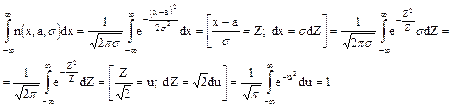
Найдем выражение для производящей функции нормального распределения

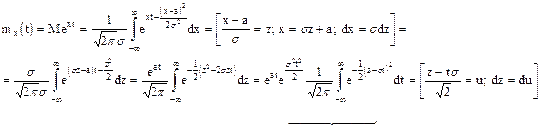
=1 (интеграл Эйлера)

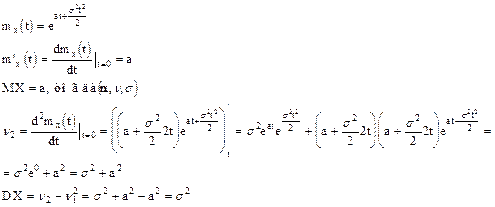
Изобразим примерный вид плотности

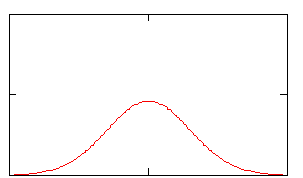
Рассмотрим центрированную нормальную величину, т.е. MX=0

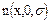
У центральной нормированной величины все нечетные начальные моменты равны 0

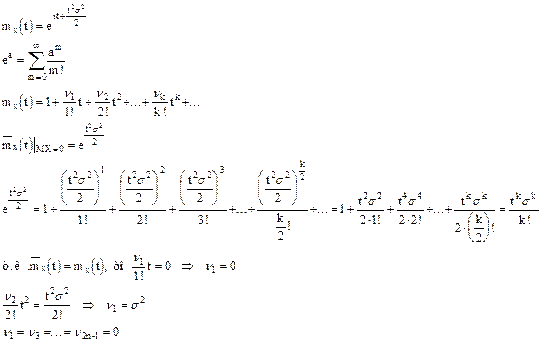
Функция Лапласа

Функцией Лапласа называется функция вида

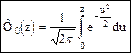
Свойства:

1) при z>0 функция Лапласа определяет вероятность попадания нормальной случайной величины с параметрами

MX=0

DX=1

в интервале (0, z)

2)

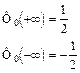
3) 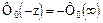- функция нечетная

Иногда в литературе встречаются два вида функций Лапласа

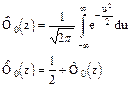
Функция Лапласа табулирована. Функция Лапласа используется для выполнения событий вида

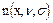
для произвольных нормальных величин.

Найдем вероятность того, что в результате испытания над x произойдет сложное событие: x примет числовое значение, принадлежащее отрезку с концами (a, b).

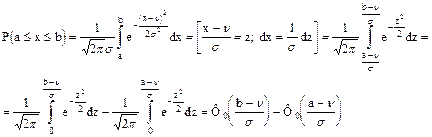
Пример.

x - случайная величина.

f(x) - плотность вероятности.

Найти плотность вероятности g(n) случайной величины H.

Рассмотрим отрезок (h, h+dh). Событию попадание H в отрезок (h, h+dh) в силу однозначности функции h(x) соответствует попадание x в отрезок (x, x+dx). При этом вероятности наступления такого события одинаковы:

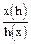
Тогда построим функцию h(x), обратную x(h), x=x(h).

т.к.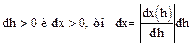

Вероятность первого события равна

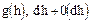
Вероятность второго события

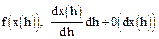
Следовательно

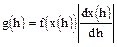
Неравенство Чебышева

Рассмотрим случайную величину X с конечным мат. ожиданием и дисперсией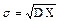

Для любого неотрицательного числа t вероятность наступления события

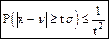
Пусть Z - непрерывная случайная величина с плотностью вероятности f(Z). Пространство событий величины Z (0; ¥). Тогда имеет место неравенство

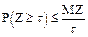
Доказать неравенства

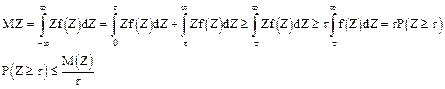
Рассмотрим два сложных события

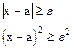
a - произвольное действительное число.

Показать самим, что x - удовлетворяет и одному и другому неравенству.

Тогда 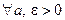справедливо

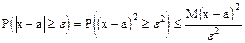
В данном случае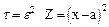

Равномерность неравенств при e>0

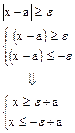
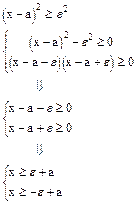
или, в частности, при a=n=MX

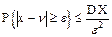
при e=st справедливо неравенство Чебышева.

Многомерные случайные величины.

Инженерная интерпретация.

Проводится испытание. В результате испытания фиксируется m числовых значений X₁, X₂, ...,X_m. Исход испытания случайный.

Пример: Испытание - реализация некоторой технологии выпуска продукта. Исход - численное значение m характеристик, оценив которые мы оценим качество продукта.

Т.к. в процессе реализации технологии на технологию действуют случайные факторы, то результат испытания неоднозначен.

Аксиоматика. Формальная вероятностная модель.

Имеется вероятностное пространство: (W, s, P). Зададим m числовых измеримых скалярных функций x₁(w), ..., x_m(w). Каждая из этих функций является одномерной по определению. Возьмем m произвольных действительных чисел и рассмотрим событие A.

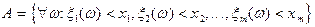
Очевидно, что событие A является пересечением событий A_i вида:

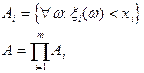
Т.к. каждое A_iÎs-алгебре, то и AÌs-алгебре. Следовательно, существует вероятность наступления события A и существует числовая скалярная функция m действительных аргументов, которая определена для всех значений своих аргументов и численно равна вероятности наступления события A.

F(x₁, x₂, ...,x_m)=P(A)

Это m-мерная функция распределения m-мерной случайной величены.

Свойства многомерного распределения:

1. Значение функции при значении хотя бы одного ее аргумента равного -¥, равно 0, как вероятность невозможного события.

2. Значение функции, при всех значениях ее аргументов равных +¥, равно 1, как вероятность достоверного события.

3. Функция не убывает по любой совокупности ее аргументов.

4. Функция непрерывна почти всюду (для инженерной практики это означает, что на конечном, либо счетном множестве аргументов она может иметь скачки 1-го рода).

Рассмотрим арифметическое пространство 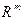и зададим полуинтервалы вида:

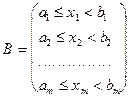
Доказать самим, что P(B) существует, и образ этого множества принадлежит s-алгебре по w.

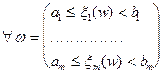
Можно доказать, что:

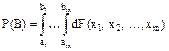
Т.о. многомерная функция распределения позволяет в m-мерном арифметическом пространстве задать счетно-аддитивную меру - функцию на поле, порожденному всеми m-мерными полуинтервалами объема ("i, a_i¹b_i). Тогда построим минимальную s-алгебру на этом поле, которая называется борелевским полем (алгеброй) в m-мерном арифметическом пространстве. Любая скалярная функция m-аргументов удовлетворяет всем свойствам, приведенным для m-мерной функции распределения и однозначно задает вероятностное пространство вида:

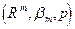
Таким образом, для инженерного исследования задача свелась к следующему: пространство элементарных событий - это m-мерное арифметическое пространство. По результатам статистических испытаний нужно оценить m-мерную функцию распределения F(x₁, x₂, ...,x_m). Рассмотрим числовую скалярную функцию m действительных аргументов. g(x₁, x₂, ...,x_m). Функция g(x₁, x₂, ...,x_m) называется борелевской, если для любого BÌb в одномерном арифметическом пространстве соответствующая 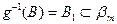. Тогда справедлива теорема, доказательство которой полностью повторяет доказательство в одномерном случае. Скалярная функция 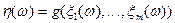- является измеримой скалярной функцией - случайной величиной.

Двумерные случайные величины.

Рассмотрим испытание, результатом которого является появление двух чисел из некоторого конечного либо счетного множества пар чисел. Это испытание физически может быть одним испытанием (мгновенное измерение прибором величены тока и напряжения в сети), а также может быть композицией двух испытаний, каждое из которых порождает одномерную дискретную величину. Условно двумерная дискретная случайная величина обозначается как XY, либо любые две буквы латинского алфавита, либо для: X:{x₁, x₂, ...,x_s}, Y:{y₁, y₂, ...,y_n}, проводя испытание над двумерной случайной величиной находят одно из чисел из X либо из Y. А вероятностное пространство двумерной случайной величены формально строится так:

Двумерной случайной величиной называется система из двух одномерных случайных величин X, Y, где как X, так и Y являются дискретными случайными величинами. В пространстве элементарных событий дискретной случайной величены XY определим сложное событие A: В результате испытания над двумерной случайной величиной XY, случайная величина X приняла значение x_i, случайная величина Y - любое значение.

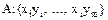
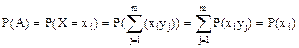
Вводим сложное событие B: В результате испытания над двумерной случайной величиной XY, случайная величина Y приняла значение y_j­.

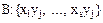
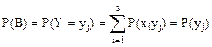
Найдем условную вероятность:

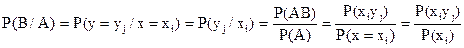
Аналогично:

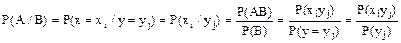
Покажем что сумма условных вероятностей: ;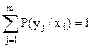

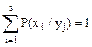
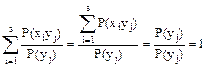
Условным математическим ожиданием является выражение:

;

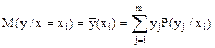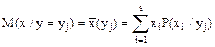
Условной дисперсией называется выражение:

;

.

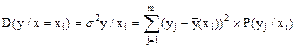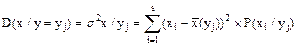Условное мат. ожидание и дисперсия отличаются от безусловной только тем, что в их определении подставляется условная вероятность вместо безусловной.

Условное мат. ожидание случайной величены, при условии, что другая случайная величена приняла заданное значение определяет число-точку, относительно которой группируются результаты конкретных испытаний над одной случайной величиной, при условии, что в этом испытании (над двумерной случайной величиной XY) вторая случайная величена приняла заданное фиксированное значение.

Условная дисперсия определяет степень концентрации результатов конкретных испытаний над одной случайной величиной относительно условного мат. ожидания.

При решении практических задач условное мат ожидание и условная дисперсия обычно используются в следующем случае: проводят испытание над X и Y, исследователь имеет возможность измерять результаты испытания над одной случайной величиной, измерение другой недоступно. Если условные дисперсии малы, то в качестве неизвестного значения не измеряемой случайной величены, которую она приняла в результате испытания, можно брать мат. ожидание.

Двумерные непрерывные случайные величины.

Двумерная случайная величина называется непрерывной случайной величиной, если пространством ее элементарных событий является плоскость, либо область плоскости, либо область конечной ненулевой плоскости. Очевидно что X и Y являются одномерными непрерывными случайными величинами.

Следствием этого определения является следующее: любое сложное событие размерности 1 (произвольная кривая, принадлежащая пространству элементарных событий) имеет нулевую вероятность т.к. в противном случае вероятность достоверного события никогда бы не равнялась единице. Числовая скалярная функция двух действительных аргументов называется двумерной плотностью вероятности, двумерной случайной величины XY, если для фиксированных значений своих аргументов она выполняет равенство 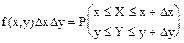. Приведенное здесь определение является аналогичным определению одномерной плотности вероятности.

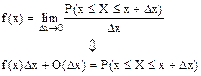
Ниже будет выведено условие существования плотности вероятности для фиксированных x, y.