Расчет сложной цепи постоянного тока

Первый и второй законы Кирхгофа для расчета цепей, правила

составления уравнений

Расчеты таких цепей производят на основе уравнений Кирхгофа.

Первый закон Кирхгофа говорит о том, что в любой момент времени количество электрических зарядов, направленных к узлу, равно количеству зарядов, направленных от узла, откуда следует, что электрический заряд в узле не накапливается. Поэтому алгебраическая сумма токов в ветвях, сходящихся в узле электрической цепи, равна нулю:

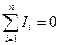(1), где n — число ветвей, сходящихся в узле.

До написания уравнения (1) необходимо задать условные положительные направления токов в ветвях, обозначив эти направления на схеме стрелками. В уравнении (1.18) токи, направленные к узлу, записывают с одним знаком (например, с плюсом), а токи, направленные от узла, с противоположным знаком (с минусом).

Приведем пример рис.2. 3. I₁ – I₂ + I₃ – I₄ = 0.

I₁

I₂

I₃ I₄

Рис.2.3

Второй закон Кирхгофа отражает положение о том, что изменение потенциала во всех элементах контура в сумме равно нулю. Из этого следует такая формулировка второго закона Кирхгофа: в любом замкнутом контуре электрической цепи постоянного тока алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех элементах этого контура:

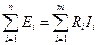(2), где n – число ЭДС в контуре; m – число элементов с сопротивлением 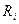в контуре.

При составлении уравнений по второму закону Кирхгофа предварительно задают условные положительные направления токов во всех ветвях электрической цепи и для каждого контура выбирают направление обхода. Если при этом направление ЭДС совпадает с направлением обхода контура, то такую ЭДС берут со знаком плюс, если не совпадает — со знаком минус. Падения напряжений в правой части уравнения (2) берут со знаком плюс, если положительное направление тока в данном элементе цепи совпадает с направлением обхода контура, если не совпадает — со знаком минус.

Пример

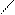
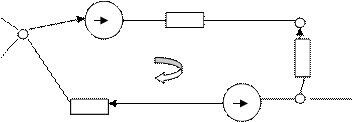
Рис. 2.4

Уравнение для замкнутого контура: I₁R₁ – I₂R₂ + I₃R₃ = E₁ – Е₃

Типичная задача расчета цепи заключается в нахождении токов в ветвях при заданных ЭДС и сопротивлениях нагрузок. Для этого составляются уравнения по законам Кирхгофа. Число уравнений должно соответствовать числу неизвестных.

Пусть электрическая цепь имеет «q» число узлов и «p» число ветвей. Теория говорит, что по первому закону Кирхгофа можно составить«q – 1» число нетождественных уравнений. Тогда по второму закону Кирхгофа нужно составить «p – q + 1» независимых уравнений, что всегда возможно (так говорит теория).

Таким образом, используя законы Кирхгофа можно рассчитать цепь любой сложности. В качестве примера приведем эквивалентную схему зарядки аккумулятора Е₂ с внутренним сопротивлением R₂. Балластное сопротивление R₃ сглаживает пульсации, возникающие в процессе электролиза.

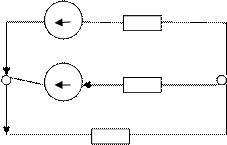Е₁ R₁

Одно уравнение для узла: I₁ + I₂ – I₃ = 0

I₁ Для контуров два уравнения, составляются

E₂ R₂ против часовой стрелки.

A Весь внешний контур: I₁R₁ + I₃R₃ = E₁

I₂ Контур с двумя ЭДС: I₁R₁ – I₂R₂ = E₁ – Е₂

I₃

R₃ Рис. 2.5

Если в результате расчета какой-то ток получится с отрицательным знаком, это значит, что мы неверно выбрали первоначальное направление, и он на самом деле течет в противоположном направлении.