Оценка аннуитетов

Одно из ключевых понятий в финансовых и коммерческих расчетах – понятие аннуитета. Логика, заложенная в схему аннуитетных платежей, широко используется при оценке долговых и долевых ценных бумаг, в анализе инвестиционных проектов, а также в анализе аренды.

Аннуитет представляет собой частный случай денежного потока, в котором денежные поступления в каждом периоде одинаковы по величине. Если число равных временных интервалов ограничено, аннуитет называется срочным. В этом случае:

С₁ = С₂ = … = С_n = A

Для оценки будущей и приведенной стоимости аннуитета можно пользоваться вышеприведенными формулами (4.16. – 4.19.), вместе с тем благодаря специфике аннуитетов в отношении равенства денежных поступлений эти формулы могут быть существенно упрощены. В частности, для решения прямой задачи оценки срочных аннуитетов постнумерандо и пренумерандо при заданных величинах регулярного поступления (А) и процентной ставке (r) можно воспользоваться такими формулами:

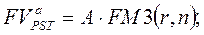(4.20.)

(4.21.)

где (4.22.)

Экономический смысл FM3 (r,n), называемого мультиплицирующим множителем для аннуитета, заключается в следующем: он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу к концу срока его действия. Предполагается, что денежные суммы лишь начисляются, а изъять их можно по окончании срока действия аннуитета. Множитель FM3 (r,n) часто используют в финансовых вычислениях и он также табулирован.

Для решения обратной задачи оценки срочных аннуитетов постнумерандо и пренумерандо, являющейся основной при анализе инвестиционных проектов, денежные притоки которых имеют вид аннуитетных поступлений, можно воспользоваться следующими формулами:

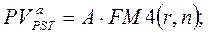(4.23.)

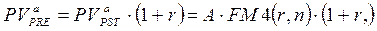(4.24.)

где (4.25.)

Экономический смысл FM4 (r,n), называемого дисконтирующим множителем для аннуитета, заключается в следующем: он показывает, чему равна с точки зрения текущего момента величина аннуитета с регулярными денежными поступлениями в размере одной денежной единицы, продолжающегося n равных периодов с заданной процентной ставкой r. Значения этого множителя также табулированы.

При выполнении некоторых расчетов применяют технику оценки бессрочного аннуитета, под которым понимаются денежные поступления, продолжающиеся достаточно длительное время (аннуитеты, рассчитанные на 50 и более лет).

В этом случае прямая задача смысла не имеет. Что касается обратной задачи, то ее решение находится на основе формулы:

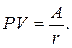(4.26.)

Эта формула служит для оценки целесообразности приобретения бессрочного аннуитета. В данном случае должен быть известен размер годовых поступлений; в качестве коэффициента дисконтирования r обычно принимают гарантированную процентную ставку (например, процент, предлагаемый государственным банком).