Координатных диаграмм

Наиболее распространенным и удобным способом графического изображения абсолютных и относительных показателей динамики, показателей сравнения и др. считается координатнаядиаграмма.

Координатные диаграммы базируются на применении системы прямоугольных координат. Перед ее построением целесообразно обратить внимание на важнейшее требование, которое заключается в соблюдении оптимального соотношения длины координатных осей, т.е. между высотой и основанием координатной диаграммы. Если это соотношение берётся произвольно, т.е. одни и те же данные на графике будут представлены как в виде чрезмерно высокой, или неоправданно низкой диаграммы, то искажение неизбежно. В связи с этим ставится закономерный вопрос: какое же соотношение длины высоты и основания надо считать нормальным? Этот вопрос легко решается на основе принципа золотого сечения. Сущность его в том, что некоторый отрезок делится на две неравные части в таком соотношении, что отношение всего отрезка к его большей части примерно равняется отношению большей части к меньшей. Например, если отрезок, состоящей из 13 единиц, разделить по принципу золотого сечения, то большая его часть будет равна 8, а меньшая – 5 единицам. В этом случае получаем следующую пропорцию: 13 : 8 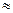8 : 5. Отсюда отношение 5:8 и может рассматриваться в качестве оптимального между высотой и основанием координатных диаграмм. Практически рациональное соотношение длины координатных осей должно соответствовать пропорции ОУ: ОХ 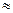1: 1,4 – 1,5. Это означает, что если длина оси ОУ=10 см, то ОХ –14 – 15 см.

Нередко при построении координатных диаграмм допускается существенная ошибка в виде чрезмерно высокой, или низкой диаграммы, т.е. в первом случае создается иллюзия колоссального возрастания статистического показателя, а во втором – его неоправданного замедления.

Важная особенность координатных диаграмм заключается в том, что они требуют двух масштабов, каждому из которых соответствуют определенные значения признаков. При этом факторный признак размещают на горизонтальной оси (абсцисс), результативный – на вертикальной оси (ординат). Горизонтальная и вертикальная оси в координатной диаграмме являются ее масштабными шкалами. Масштабная шкала координатной диаграммы – сочетание прямой линии, меток и чисел отсчёта, соответствующих ряду последовательных значений изображаемого показателя. Масштабная шкала может быть равномерной и неравномерной; ее целесообразно градуировать, но подписывать значение определённых точек необходимо только в тех случаях, когда они приходятся на «круглые» числа.

Статистическую информацию, как правило, не следует указывать ни на масштабной шкале, ни где-либо внутри графика. График призван заменить цифры, и поэтому нецелесообразно его перегружать цифровыми данными. Наиболее распространенным и удобным способом графического изображения абсолютных или относительных показателей динамики считается линейнаяразновидность координатной диаграммы. Эта линия, отражающая совокупность точек, расположенных на плоскости в местах пересечения значений независимого (факторного) и зависимого (результативного) признаков. При построении линейной диаграммы важно помнить о том, что на оси абсцисс (ОХ) размещается шкала независимой переменной, а на оси ординат (ОУ) – зависимой переменной величины. Если в динамике некоторые периоды или моменты времени оказались пропущены, то это должно быть учтено при построении диаграммы. Равным периодам должны соответствовать равные отрезки масштабной шкалы. Во многих случаях для лучшего проявления характера динамики рекомендуется при построении вертикальной шкалы отказаться от использования нулевой точки. С этой целью рассчитывают рациональный масштаб, для чего необходимо вертикальную ось графика разделить на «круглое» число отрезков (например, 5,10 и т.д.). Далее проводят расчёт масштаба по результативному признаку:

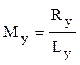, (5.1)

где М_у – масштаб зависимой переменной (результативного показателя); R_y – размах колебаний в абсолютных или относительных показателях динамики (У_max – У_min); L_у – намеченное «круглое» число отрезков, отмеченных на вертикальной оси.

Рассчитанный по формуле 5.1 масштаб представляет собой то значение показателя динамики, которое содержится в каждом отрезке. При таком способе построения линейной диаграммы целесообразно показать разрез вертикального масштаба, а полученная на диаграмме линия отчётливее, рельефнее отражает динамическое развитие, о чём свидетельствует, например, графическое изображение динамики посевных площадей озимого рапса в сельскохозяйственной организации (рис. 5.1).

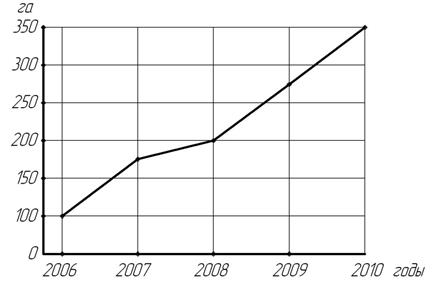
Рис. 5.1. Динамика посевных площадей озимого рапса (линейная диаграмма)