Метод прогонки для решения разностной схемы.

Система (7.9) – (7.10) является системой линейных алгебраических уравнений с N-1 неизвестными. Полученная задача решается методом прогонки.

Пусть

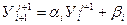. (7.12)

После подстановки в (7.11) получится рекуррентная формула

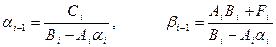(7.13)

Для определения преобразуя (7.10) приводим его к виду

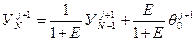(7.14)

где

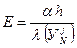
Сравнивая (7.14) с (7.12) получаем, что

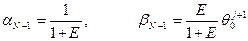(7.15)

Теперь из (7.12) , (7.15) определяются все

После этого рассматривая совместно (7.12) и (7.9) вычисляются все

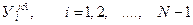
В данном случае все условия теоремы 2 из §4 выполняются, поэтому метод прогонки для решения задачи (7.9) – (7.11) является устойчивой.