Математическая модель
Строго говоря, решение этой задачи приводит к дифференциальному уравнению с частными производными, так как температура в поперечном сечений трубопровода не вполне постоянна и является функцией расстояния х и расстояния поверхности стержня.
Однако, если трубопровод достаточно тонкий и если теплопроводность его велика, то мы можем без существенной ошибки пренебречь температурными градиентами в направлениях перпендикулярных к оси трубопровода и принять температуру постоянной в каждой точке поперечного сечения, перпендикулярного оси Ох. При таком допущении температура является функцией только одного независимого переменного х и распределение температуры может быть описано обыкновенным дифференциальным уравнением.
Пусть длина стержня равна l м, периметр поперечного сечения p м, площадь поперечного сечения Q м2. Исследуем процесс распространения тепла в элементарном отрезке длиной dx на расстоянии х от того конца стержня, температура которого t1. Количество тепла проходящего за время dt через сечение трубопровода находящееся на расстоянии х от начало трубопровода, согласно теории теплопередачи, будет равно:
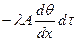
Количество тепла, прошедшее за время dt через сечение, находящееся на расстоянии х + dx от начала, будет равна:
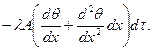
Участок стержня, заключенный между сечениями, отстоящими от начала на расстояниях х и х + dx, вследствие теплопроводности, приобретает за время dt количество тепла, равное разности указанных количеств, т.е.:
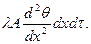
За то же время потеря тепла от этого же участка в окружающую среду будет равна:
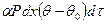
Но так как изучаемый нами процесс является стационарным, то:
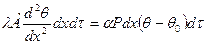
Окончательно мы приходим к следующему дифференциальному уравнению:
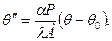
В итоге получена задача:
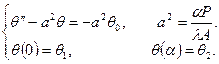
Это уравнение с постоянными коэффициентами. Его общий интеграл будет:
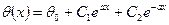
Используя граничные условия, составим систему:
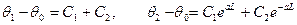
откуда
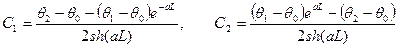
Подставляя значения С1 и С2 получим:
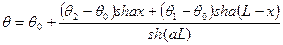
Выделим элемент длины dх, находящийся на расстояний х от левого конца, и примем его температуру равной 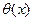 . За время ∆t через левую границу этого элемента пройдет количество тепла
. За время ∆t через левую границу этого элемента пройдет количество тепла
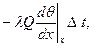
а через правую на расстоянии х+dх от конца
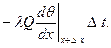

Таким образом, выделенный участок приобретает за время 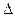 t количество тепла, равное разности
t количество тепла, равное разности
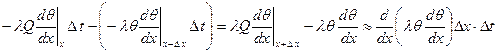 .
.
Вместе с тем потеря тепла этого элемента через поверхности в окружающую среду равна
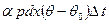 .
.
Вследствие предположения о стационарности процесса эти количества равны, т.е.
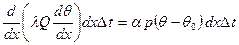
откуда
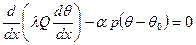 (4.1)
(4.1)
Пусть на обоих концах стержня поддерживается постоянная температура 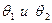 . Тогда краевые условия имеют вид.
. Тогда краевые условия имеют вид.
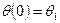 ,
, 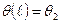 (4.2)
(4.2)
Численный пример. Пусть a = 10 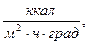
l = 300 ккал/м×час×град
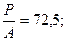 тогда
тогда 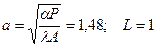

При этом случае получится зависимость
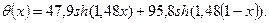
4.3. Приближенный метод решения задачи (4.1) – (4.2)
Отрезок 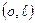 разбиваем на n равных частей с шагом
разбиваем на n равных частей с шагом 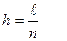 . Тогда получится сетка
. Тогда получится сетка 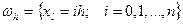 .
.
Обозначим 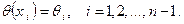
Мы знаем, что
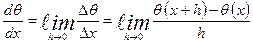

При малых h справедливо соотношение
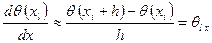
или
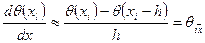
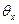 - правая разностная производная,
- правая разностная производная, 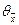 - левая разностная производная.
- левая разностная производная.
Аналогично получится приближенная формула
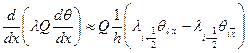
т.е. считаем, что площадь поперечного сечения Q постоянная величина вдоль трубопровода. На основе этих формул из (4.1) получается приближенное неравенство.
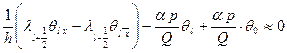
Предполагая, что h малая величина составляем равенства
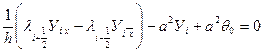 (4.3)
(4.3)
i=1, 2, …, n-1.
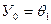 ,
, 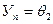 . (4.4)
. (4.4)
где 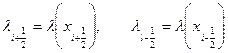 .
.
(4.3) – (4.4) является разностной задачей.
Теорема – 1. Если 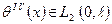 , то решение разностной задачи (4.3) – (4.4) сходится к решению (4.1) – (4.2) при
, то решение разностной задачи (4.3) – (4.4) сходится к решению (4.1) – (4.2) при 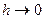 и справедливо неравенство
и справедливо неравенство
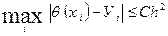 (4.5)
(4.5)
где C- константа, зависящая от начальных данных.
Из (4.5) становится ясно, что при малом h в качестве 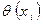 можно взять решение приближенной задачи (4.3) – (4.4).
можно взять решение приближенной задачи (4.3) – (4.4).
4.4. Трехточечная разностная схема. Метод прогонки
Из (4.3) – (4.4) получаем равенства
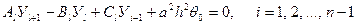 (4.6)
(4.6)
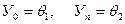
где
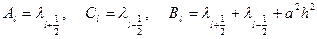 .
.
(4.6) – называется трехточечной разностной схемой. Это есть система n-1 линейных алгебраических уравнений c 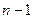 неизвестными. Данная система имеет единственное решение.
неизвестными. Данная система имеет единственное решение.
Система (4.6) решается методом прогонки. Предполагаем, что решение (4.6) имеет вид
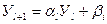 (4.7)
(4.7)
Подставляем его в (4.6). Тогда,
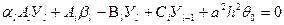
или
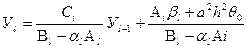 (4.8)
(4.8)
Сравнивая (4.7) и (4.8) получим соотношения
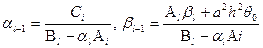 (4.9)
(4.9)
Из (4.7) при l = n-1 получим
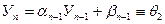 .
.
Из этого тождества получим
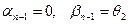 . (4.10)
. (4.10)
Из (4.9) и (4.10) определяются все
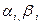 i = n-2, n -3, …, 0.
i = n-2, n -3, …, 0.
После этого из (4.7) используя 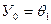 определяются все
определяются все
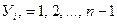 .
.
Теорема 2.Если 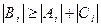 и
и 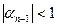 , то метод прогонки является устойчивой. То есть, при реализаций схемы ошибки округления не накапливаются.
, то метод прогонки является устойчивой. То есть, при реализаций схемы ошибки округления не накапливаются.
В нашем случае оба неравенства выполняются, поэтому метод прогонки является устойчивым.
Дата добавления: 2015-02-13; просмотров: 775;
