Математическая модель задачи.
Текущая обводненность продукции скважин определяется следующим соотношением: 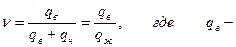 дебит воды, добываемой одновременно с нефтью из всех скважин;
дебит воды, добываемой одновременно с нефтью из всех скважин;
qн – дебит нефти.
Понятно, что 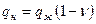 . Так как кривая на рис.3.1 выражает зависимость
. Так как кривая на рис.3.1 выражает зависимость 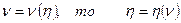 .
.
Поскольку 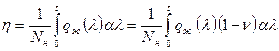 получим
получим 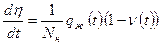 . Из предыдущего равенства имеем
. Из предыдущего равенства имеем

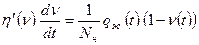 . или
. или 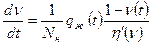 . (3.1)
. (3.1)
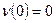 . (3.2)
. (3.2)
Полученная задача Коши (3.1) – (3.2) решается различными численными методами.
Теория вытеснения нефти водой, развитая Баклеем и Левереттом, изложена в [4]. В качестве аппроксимирующей функций зависимости приведенной в рис.6 используем выражение
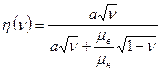 (3.3)
(3.3)
(3.3) называется функцией Баклея – Леверетта, где а – положительная константа.
3.3.Численные методы решения задачи (3.1) – (3.2)
Поясним основные понятия, возникающие при использовании численных методов.
Введем по переменной t равномерную сетку с шагом h>0, т.е. рассмотрим множество точек 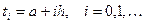 .
.
1. Метод Эйлера. Уравнение (3.1) заменяется разностным уравнением
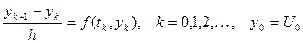 .
.
Где 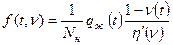
Решение этого уравнения находится явным образом по рекуррентной формуле 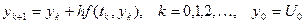 .
.
Погрешность метода. 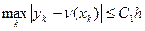 , где
, где 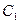 – константа, зависящая от правой части дифференциального уравнения (3.1). В этом случае метод имеет первый порядок точности.
– константа, зависящая от правой части дифференциального уравнения (3.1). В этом случае метод имеет первый порядок точности.
2. Метод Рунге – Кутта второго порядка точности.
Предположим, что приближенное значение 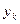 решение исходной задачи в точке
решение исходной задачи в точке 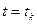 уже известно. Для нахождения
уже известно. Для нахождения 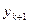 поступим следующим образом. Сначала, используя схему Эйлера
поступим следующим образом. Сначала, используя схему Эйлера 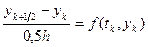 вычислим промежуточное значение
вычислим промежуточное значение 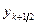 , а затем воспользуемся разностным уравнением
, а затем воспользуемся разностным уравнением 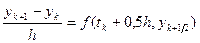 , из которого явным образом найдем искомое значение
, из которого явным образом найдем искомое значение 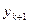 .
.
Погрешность метода. 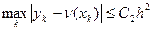 , где
, где 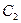 – константа, зависящая от исходных данных (3.1). Этот метод имеет второй порядок точности.
– константа, зависящая от исходных данных (3.1). Этот метод имеет второй порядок точности.
3. Метод Рунге – Кутта третьего порядка точности.
Считаем, что решение задачи (3.1) – (3.2) в точке 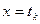 уже известно. Тогда решение задачи (3.1) – (3.2) определяется по следующей схеме:
уже известно. Тогда решение задачи (3.1) – (3.2) определяется по следующей схеме:
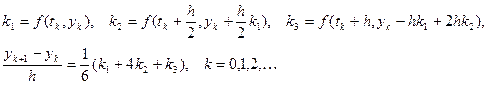
Погрешность метода.
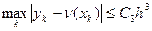 , где
, где 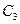 – константа, не зависящая от к.
– константа, не зависящая от к.
4. Метод Рунге – Кутта четвертого порядка точности.
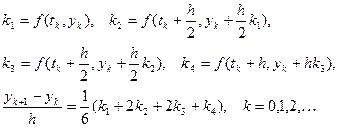
Погрешность метода.
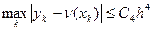 , где
, где 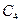 – константа, зависящая от начальных данных и не зависящая от к.
– константа, зависящая от начальных данных и не зависящая от к.
Замечание: Метод Рунге-Кутта также применяется, если неизвестная функция является вектором, т.е.
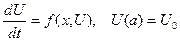 , где
, где 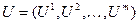 .
.
Дата добавления: 2015-02-13; просмотров: 766;
