Индексы средних величин
В ряде случаев приходится изучать динамику общественных явлений, уровни которых выражены средними величинами (средней себестоимостью, средней заработной платой, средней урожайностью, средней производительностью труда и т.д.).
Динамика средних показателей зависит от одновременного изменения вариантов, из которых формируются средние, и изменения удельных весов этих вариантов, т.е. от структуры изучаемого явления. Так, например, средняя производительность труда на предприятии может возрасти за счет ее повышения у рабочих отдельных специальностей и повышения удельного веса рабочих с более высокой производительностью труда в общей численности рабочих.
Таким образом, на изменение динамики среднего значения изучаемого явления могут оказывать влияние одновременно два фактора: изменение осредняемого показателя и изменение структуры. Изучение совместного действия указанных факторов на общее изменение динамики среднего уровня явления, а также роли и влияния каждого фактора в отдельности в общей динамике средней проводится в статистике при помощи системы взаимосвязанных индексов, которую можно представить в следующем виде:
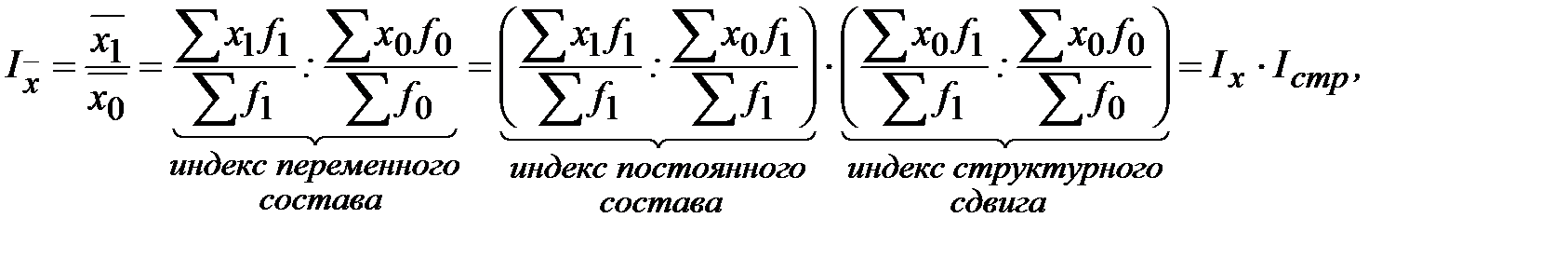 где
где 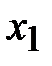 и
и 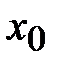 – уровни осредняемого показателя соответственно в отчетном и базисном периодах, а
– уровни осредняемого показателя соответственно в отчетном и базисном периодах, а 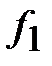 и
и 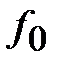 – веса (частоты) осредняемых показателей соответственно в отчетном и базисном периодах.
– веса (частоты) осредняемых показателей соответственно в отчетном и базисном периодах.
В указанной системе взаимосвязанных индексов при построении индекса постоянного состава в качестве весов принята структура отчетного периода, что позволяет проследить изменение средней динамики изучаемого явления только за счет изменения осредняемых значений качественного показателя. При построении индекса структурных сдвигов в качестве соизмерителя принята величина осредняемого показателя на уровне базисного периода, что дает возможность изучить изменение средней динамики явления только за счет структурных сдвигов.
Используя индексы средних величин, можно найти не только относительное влияние факторов, но и определить абсолютное изменение уровня среднего показателя в целом ( 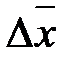 ) и за счет каждого из факторов: за счет непосредственного изменения уровней осредняемого признака (
) и за счет каждого из факторов: за счет непосредственного изменения уровней осредняемого признака ( 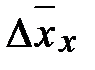 ) и за счет изменения структуры (
) и за счет изменения структуры ( 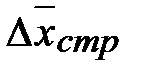 ). Для этого необходимо из числителя соответствующего индекса приведенной системы индексов вычесть его знаменатель. Итак
). Для этого необходимо из числителя соответствующего индекса приведенной системы индексов вычесть его знаменатель. Итак
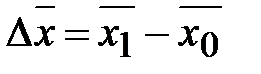 ,
,
в том числе:
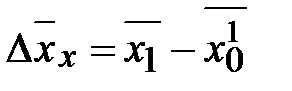 ;
;
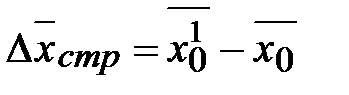 ;
;
Таким образом 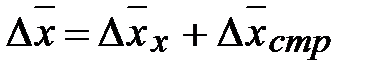 .
.
Дата добавления: 2015-02-13; просмотров: 761;
