Расчет прямозубых цилиндрических передач на прочность
Расчет на прочность прямозубых и косозубых цилиндрических передач стандартизован ГОСТ 21354-87.
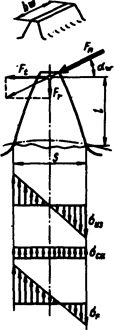
Силы в зацеплении. На рис. 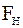 - нормальная сила, направленная по линии зацепления как общей нормали к рабочим поверхностям зубьев. Силы, действующие в зацеплении, принято прикладывать в полюсе зацепления. При этом силу -
- нормальная сила, направленная по линии зацепления как общей нормали к рабочим поверхностям зубьев. Силы, действующие в зацеплении, принято прикладывать в полюсе зацепления. При этом силу - 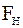 , переносят в полюс и раскладывают на окружную
, переносят в полюс и раскладывают на окружную 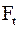 , и радиальную
, и радиальную 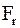 . По заданным
. По заданным 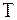 и
и 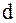 определяют
определяют
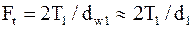
и через нее выражают все другие составляющие:
, .
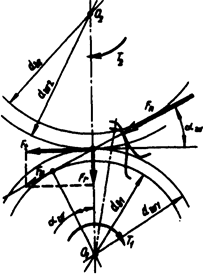
Расчет прочности зубьев по контактным напряжениям. Наименьшей контактной усталостью обладает околополюсная зона рабочей поверхности зубьев, где наблюдается однопарное зацепление (см. рис.). Поэтому расчет контактных напряжений принято выполнять при контакте в полюсе зацепления. Контакт зубьев можно рассматривать как контакт двух цилиндров с радиусами 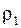 и
и 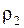 . При этом контактные напряжения определяют по формуле
. При этом контактные напряжения определяют по формуле
 .
.
Для прямозубых передач
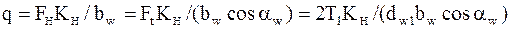 /
/
Радиусы кривизны эвольвент зубьев в точке контакта (рис. 8.18)
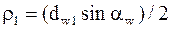 ;
; 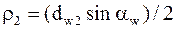 .
.
По формуле
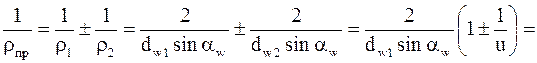
|
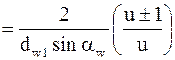 ,
,
где 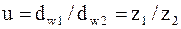 , знак «+» - для наружного, а «-» - для внутреннего зацепления.
, знак «+» - для наружного, а «-» - для внутреннего зацепления.
(8.7) Заменяя

и подставляя в формулу получаем
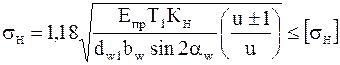 .
.
Параметр 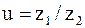 по ГОСТ 16532-70 называют передаточным числом и определяют как отношение большего числа зубьев к меньшему независимо от того, как передается движение: от
по ГОСТ 16532-70 называют передаточным числом и определяют как отношение большего числа зубьев к меньшему независимо от того, как передается движение: от 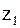 к
к 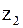 или от
или от 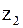 к
к 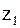 . Это передаточное число
. Это передаточное число 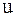 отличается от передаточного отношения
отличается от передаточного отношения 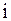 , которое равно отношению угловых скоростей ведущего колеса к ведомому и которое может быть меньше или больше единицы, положительным или отрицательным. Применение
, которое равно отношению угловых скоростей ведущего колеса к ведомому и которое может быть меньше или больше единицы, положительным или отрицательным. Применение 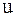 вместо
вместо 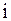 связано только с принятой формой расчетных зависимостей для контактных напряжений [см. вывод формулы (8.9), где
связано только с принятой формой расчетных зависимостей для контактных напряжений [см. вывод формулы (8.9), где 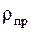 выражено через
выражено через 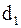 (меньшее колесо), а не через
(меньшее колесо), а не через 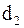 (большее колесо)]. Величина контактных напряжений, так же как и передаточное число
(большее колесо)]. Величина контактных напряжений, так же как и передаточное число 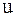 , не зависит от того, какое колесо ведущее, а величина передаточного отношения зависит
, не зависит от того, какое колесо ведущее, а величина передаточного отношения зависит 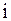 . Однозначное определение
. Однозначное определение 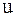 позволяет уменьшить вероятность ошибки при расчете. Передаточное число
позволяет уменьшить вероятность ошибки при расчете. Передаточное число 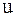 относится только к одной паре зубчатых колес. Его не следует применять для обозначения передаточного отношения многоступенчатых редукторов, планетарных, цепных, ременных и других передач. Там справедливо только обозначение
относится только к одной паре зубчатых колес. Его не следует применять для обозначения передаточного отношения многоступенчатых редукторов, планетарных, цепных, ременных и других передач. Там справедливо только обозначение 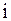 .
.
Величины расчетных контактных напряжений одинаковы для шестерни и колеса. Поэтому расчет выполняют для того из колес пары, у которого меньше допускаемое напряжение 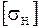 - см. ниже (чаще это бывает колесо, а не шестерня).
- см. ниже (чаще это бывает колесо, а не шестерня).
Формулу используют для проверочного расчета, когда все необходимые размеры и другие параметры передачи известны. При проектном расчете необходимо определить размеры передачи по заданным основным характеристикам: крутящему моменту 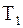 или
или 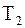 и передаточному числу
и передаточному числу 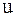 .
.
С этой целью формулу решают относительно 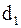 . Другие неизвестные параметры оценивают приближенно или выбирают по рекомендациям на основе накопленного опыта. В нашем случае принимаем
. Другие неизвестные параметры оценивают приближенно или выбирают по рекомендациям на основе накопленного опыта. В нашем случае принимаем 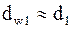 ;
; 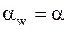 =200 (
=200 ( 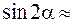 0,6428),
0,6428), 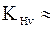 1,15 (этот коэффициент зависит от окружной скорости
1,15 (этот коэффициент зависит от окружной скорости 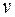 , которая пока неизвестна, поэтому принято некоторое среднее значение - см. табл. 8.3). При этом из составляющих коэффициента
, которая пока неизвестна, поэтому принято некоторое среднее значение - см. табл. 8.3). При этом из составляющих коэффициента 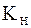 [см. формулу (8.4)] остаются
[см. формулу (8.4)] остаются 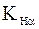 и
и 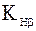 . Далее обозначаем
. Далее обозначаем 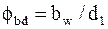 - коэффициент ширины шестерни относительно диаметра.
- коэффициент ширины шестерни относительно диаметра.
Подставляя в формулу (8.10) и решая относительно 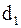 , находим
, находим
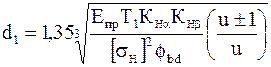 .
.
Решая относительно межосевого расстояния  , заменяем
, заменяем 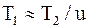 ;
; 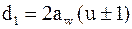 и вводим
и вводим 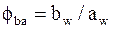 - коэффициент ширины колеса относительно межосевого расстояния.
- коэффициент ширины колеса относительно межосевого расстояния.
После преобразований с учетом зависимости
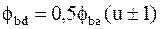
Получим
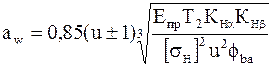 .
.
При расчетах передач с цилиндрическими зубчатыми колесами чаще используют формулу (8.13), так как габариты передачи определяет преимущественно межосевое расстояние.
Расчет значений допускаемого напряжения  . Значение
. Значение 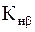 оценивают в соответствии с заданной (или выбранной) схемой передачи и значением
оценивают в соответствии с заданной (или выбранной) схемой передачи и значением 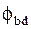 , которое рассчитывают по формуле
, которое рассчитывают по формуле 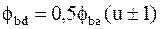 , где значение
, где значение 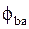 заранее выбирают по рекомендациям. При выборе учитывают следующее. Увеличение
заранее выбирают по рекомендациям. При выборе учитывают следующее. Увеличение 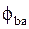 или относительной ширины колес позволяет уменьшить габариты и массу передачи, но вместе с этим требует повышенной жесткости и точности конструкции. В противном случае возрастает неравномерность распределения нагрузки по ширине зубчатого венца. Может оказаться, что положительное влияние увеличения ширины колес не компенсирует вредного влияния увеличения неравномерности нагрузки.
или относительной ширины колес позволяет уменьшить габариты и массу передачи, но вместе с этим требует повышенной жесткости и точности конструкции. В противном случае возрастает неравномерность распределения нагрузки по ширине зубчатого венца. Может оказаться, что положительное влияние увеличения ширины колес не компенсирует вредного влияния увеличения неравномерности нагрузки.
Выбор модуля и числа зубьев. В формуле
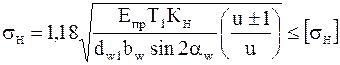
модуль и число зубьев непосредственно не участвуют. Они входят в эту формулу косвенно через 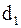 , который определяется произведением
, который определяется произведением 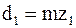 . Из этого следует, что значение контактных напряжений
. Из этого следует, что значение контактных напряжений 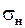 не зависит от модуля или числа зубьев в отдельности, а определяется только их произведением или диаметрами колес. По условиям контактной прочности при данном
не зависит от модуля или числа зубьев в отдельности, а определяется только их произведением или диаметрами колес. По условиям контактной прочности при данном 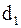 модуль передачи может быть сколь угодно малым, лишь бы соблюдалось равенство
модуль передачи может быть сколь угодно малым, лишь бы соблюдалось равенство 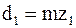 .
.
Минимально допускаемое значение модуля можно определить из условий прочности зубьев на изгиб. Однако при таком расчете в большинстве случаев получают зацепления с оченьмелкими зубьями, применение которых практически ограничено. Поэтому величину 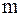 обычно выбирают, ориентируясь на рекомендации, выработанные практикой, и затем проверяют изгибную прочность зубьев. В этих рекомендациях учитывают следующее.
обычно выбирают, ориентируясь на рекомендации, выработанные практикой, и затем проверяют изгибную прочность зубьев. В этих рекомендациях учитывают следующее.
Мелкомодульные колеса с большим числом зубьев предпочтительны по условиям плавности хода передачи (увеличивается коэффициент торцового перекрытия - 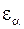 ) и экономичности. При малых
) и экономичности. При малых 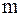 уменьшаются потери на трение (уменьшается скольжение), сокращается расход материала (уменьшается наружный диаметр
уменьшаются потери на трение (уменьшается скольжение), сокращается расход материала (уменьшается наружный диаметр 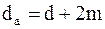 ) и экономится станочное время нарезания зубьев (уменьшается объем срезаемого материала).
) и экономится станочное время нарезания зубьев (уменьшается объем срезаемого материала).
Крупномодульные колеса с большим объемом зубьев дольше противостоят износу, могут работать длительное время после начала выкрашивания, менее чувствительны к перегрузкам и неоднородности материала (дефекты литья и т. п.). При мелком модуле возрастают требования к точности и жесткости передачи, так как увеличивается возможность поломки зубьев вследствие концентрации нагрузки, в особенности при перегрузках. При ориентировочной оценке величины 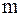 можно использовать рекомендации.
можно использовать рекомендации.
Выбрав по этой таблице 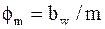 , определяют
, определяют
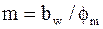 ,
,
где
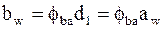 .
.
Значение 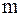 согласуют со стандартом. Для силовых передач обычно рекомендуют принимать
согласуют со стандартом. Для силовых передач обычно рекомендуют принимать 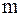 >1,0мм.
>1,0мм.
При известном модуле определяют и уточняют все остальные параметры передачи.
Для передач без смещения
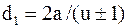 ;
; 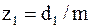 ;
; 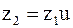 ;
;
 ;
; 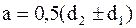 /
/
Должно быть 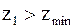 , где
, где 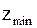 - определяют по таблице в зависимости от передачи (прямозубая, косозубая или шевронная).
- определяют по таблице в зависимости от передачи (прямозубая, косозубая или шевронная).
Для уменьшения шума в быстроходных передачах рекомендуют брать 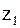 >25. Для окончательного утверждения выбранной величины модуля необходимо проверить прочность по напряжениям изгиба.
>25. Для окончательного утверждения выбранной величины модуля необходимо проверить прочность по напряжениям изгиба.
В случае неудовлетворительного результата изменяют 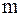 и определяют новые значения z.
и определяют новые значения z.
При проверке можно получить  значительно меньше
значительно меньше  , что не является противоречивым или недопустимым, так как нагрузочная способность большинства передач ограничивается контактной прочностью, а не прочностью на изгиб. Если расчетное значение
, что не является противоречивым или недопустимым, так как нагрузочная способность большинства передач ограничивается контактной прочностью, а не прочностью на изгиб. Если расчетное значение  превышает допускаемое, то применяют колеса, нарезанные с положительным смещением инструмента, или увеличивают
превышает допускаемое, то применяют колеса, нарезанные с положительным смещением инструмента, или увеличивают  . Это значит, что в данной передаче (при данных материалах) решающее значение имеет не контактная прочность, а прочность на изгиб. На практике такие случаи встречаются у колес с высокотвердыми зубьями при Н>50...60 HRC (например, цементированные зубья).
. Это значит, что в данной передаче (при данных материалах) решающее значение имеет не контактная прочность, а прочность на изгиб. На практике такие случаи встречаются у колес с высокотвердыми зубьями при Н>50...60 HRC (например, цементированные зубья).
|
Расчет прочности зубьев по напряжениям изгиба. Зуб имеет сложное напряженное состояние. Наибольшие напряжения изгиба образуются у корня зуба в зоне перехода эвольвенты в галтель. Здесь же наблюдается концентрация напряжений. Для того чтобы по возможности просто получить основные расчетные зависимости с учетом влияния основных параметров на прочность зубьев, рассмотрим вначале приближенный расчет, а затем введем поправки в виде соответствующих коэффициентов. Допустим следующее:
1. Нагрузка в зацеплении передается одной парой зубьев и приложена к вершине зуба. Практика подтверждает, что этот худший случай справедлив для 7-й, 8-й и более низких степеней точности, ошибки изготовления которых не могут гарантировать наличие двухпарного зацепления.
2. Зуб рассматриваем как консольную балку, для которой справедливы гипотеза плоских сечений.
Силу 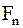 переносим по линии действия на ось симметрии зуба и раскладываем на составляющие
переносим по линии действия на ось симметрии зуба и раскладываем на составляющие 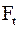 и
и 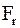 . При этом радиус приложения окружной силы
. При этом радиус приложения окружной силы 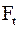 будет несколько больше радиуса начальной окружности. Пренебрегая этой разностью, для расчета сил
будет несколько больше радиуса начальной окружности. Пренебрегая этой разностью, для расчета сил 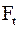 и
и 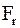 используем формулы
используем формулы
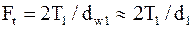
, .
Напряжение в опасном сечении, расположенном вблизи хорды основной окружности,
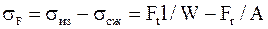
Где 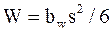 - момент сопротивления сечения при изгибе;
- момент сопротивления сечения при изгибе; 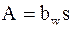 - площадь;
- площадь; 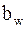 ,
, 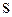 и
и  указаны на рис.
указаны на рис.
Знак «-» в формуле указывает, что за расчетные напряжения принимают напряжения на растянутой стороне зуба, так как в большинстве случаев практики именно здесь возникают трещины усталостного разрушения (для стали растяжение опаснее сжатия).
Размеры  и
и 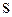 неудобны для расчетов. Используя геометрическое подобие зубьев различного модуля, их выражают через безразмерные коэффициенты:
неудобны для расчетов. Используя геометрическое подобие зубьев различного модуля, их выражают через безразмерные коэффициенты:
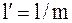 и
и 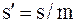 ,
,
где 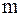 - модуль зубьев.
- модуль зубьев.
После подстановки и введения расчетных коэффициентов получают
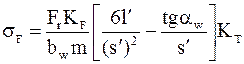 ,
,
где  - коэффициент расчетной нагрузки;
- коэффициент расчетной нагрузки; 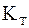 - теоретический коэффициент концентрации напряжений. Далее обозначают
- теоретический коэффициент концентрации напряжений. Далее обозначают
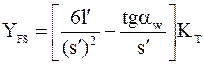
- коэффициент формы зуба.
Для колес с внутренними зубьями приближенно можно принимать 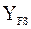 =3,5...4, большие значения - при меньших
=3,5...4, большие значения - при меньших  .
.
При этом для прямозубых передач расчетную формулу записывают в виде
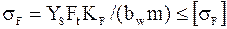 ,
,
где  - допускаемое напряжение изгиба.
- допускаемое напряжение изгиба.
Для проектных расчетов по напряжениям изгиба формулу решают относительно модуля путем замены 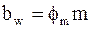 ,
, 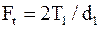 ,
, 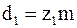 , тогда
, тогда
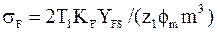
И далее, принимая приближенно 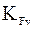 = 1,5 , получают
= 1,5 , получают
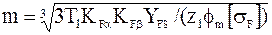
Величины 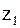 и
и 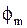 задают согласно рекомендациям.
задают согласно рекомендациям.
Из формул следует, что 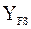 - безразмерный коэффициент, значения которого зависят только от формы зуба (
- безразмерный коэффициент, значения которого зависят только от формы зуба ( 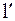 ,
, 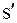 ,
, 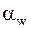 ) и в том числе от формы его галтели (коэффициент
) и в том числе от формы его галтели (коэффициент 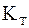 ). Форма зуба при одинаковом исходном контуре инструмента зависит от числа зубьев
). Форма зуба при одинаковом исходном контуре инструмента зависит от числа зубьев 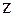 и коэффициента смещения инструмента х. Рассмотрим эту зависимость.
и коэффициента смещения инструмента х. Рассмотрим эту зависимость.
Влияние числа зубьев на форму и прочность зубьев. На рис. показано изменение формы зуба в зависимости от числа зубьев колес, нарезанных без смещения с постоянным модулем. При 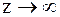 колесо превращается в рейку, и зуб приобретает прямолинейные очертания. С уменьшением
колесо превращается в рейку, и зуб приобретает прямолинейные очертания. С уменьшением 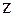 уменьшается толщина зуба у основания и вершины, а также увеличивается кривизна эвольвентного профиля. Такое изменение формы приводит к уменьшению прочности зуба. При дальнейшем уменьшении
уменьшается толщина зуба у основания и вершины, а также увеличивается кривизна эвольвентного профиля. Такое изменение формы приводит к уменьшению прочности зуба. При дальнейшем уменьшении 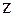 появляется подрезание ножки зуба (штриховая линия на рис., прочность зуба существенно снижается. При нарезании инструментом реечного типа для прямозубых передач число зубьев на границе подрезания
появляется подрезание ножки зуба (штриховая линия на рис., прочность зуба существенно снижается. При нарезании инструментом реечного типа для прямозубых передач число зубьев на границе подрезания 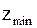 =17.
=17.

|
Рассмотренное влияние числа зубьев на прочность справедливо при постоянном модуле, когда с увеличением увеличиваются и диаметры колес. При постоянных диаметрах с изменением 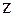 изменяется модуль
изменяется модуль 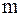 . В этом случае изменяются не только форма, но и размеры зуба. С увеличением
. В этом случае изменяются не только форма, но и размеры зуба. С увеличением 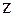 форма улучшается, а размеры уменьшаются (уменьшается
форма улучшается, а размеры уменьшаются (уменьшается 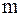 ). Уменьшение модуля снижает прочность зуба на изгиб.
). Уменьшение модуля снижает прочность зуба на изгиб.
Дата добавления: 2015-02-13; просмотров: 2378;
