Лекция 3. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.
Цель работы:исследование зависимости характеристик нитяных маятников от амплитуды колебаний, массы грузов, длины нити.
Оборудование:два нитяных маятника с подвесами (шариками различной массы), штатив с зажимом, метровая линейка с миллиметровыми делениями, секундомер, оптоэлектрический датчик, весы, разновес.
Порядок выполнения работы.
1. Установка для выполнения опыта схематически изображена на рисунке 2.
2. Определите с помощью весов массу m1, шарика, который будете подвешивать на нити, не менее пяти раз. Вычислите среднее значение массы ‹ т1›. Результаты измерений и вычислений занесите в таблицу 1.
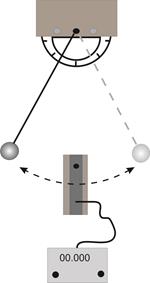
Рис.2
3. Закрепите в зажиме штатива свободный конец нити маятника таким образом, чтобы длина l, подвеса маятника (расстояние от точки подвеса до центра шарика) была не менее 1 м. Измерьте длину маятника не менее пяти раз. Вычислите среднее значение ‹l›. Результаты измерений и вычислений занесите в таблицу 1.
4. Подключите оптоэлектрический датчик к гнезду 1на задней панели цифрового секундомера. Включите прибор и переключите секундомер в режим (г P ) измерения периода колебаний.
5. Закрепите нить математического маятника в зажиме штатива.
6. Отведите шарик в сторону от положения равновесия и осторожно отпустите его и убедитесь, что свободно проходит через створ оптического датчика.
6.2(1) Исследование зависимости периода колебаний маятника от амплитуды его колебаний
1. Отведите шарик в сторону от положения равновесия и измерьте амплитуду, отпустив шарик, измерьте период колебаний маятника.
2. Повторите измерения периода при других значениях амплитуды.
3. Результаты измерений запишите в таблицу 1.
Таблица 1
| № | m1, кг | l,м | А1, м | Т1, с | А2, м | Т2, с | А3, м | Т3, с |
| среднее |
4. По результатам измерений и вычислений сделайте вывод, зависит ли период малых колебаний маятника от амплитуды его колебаний Т(А).
6.2(2) Исследование зависимости периода колебаний маятника от массы шарика
1. Измерьте массу m2 шарика второго маятника и результаты измерений занесите в таблицу 2.
2. Оставив прежнюю длину l1 маятника и амплитуду А1 колебаний измерьте не менее пяти раз период колебаний маятника.
3. Сравните среднее значение периода < Т1> и < Т4> и сделайте вывод, зависит ли период малых колебаний маятника от массы шарика.
Таблица 2
| № | m2, кг | А1, м | l1, м | Т4, с | l2, м | Т5, с | l3, м | Т6, с |
| среднее |
6.3(1) Исследование зависимости периода колебаний маятника от длины нити.
1. Оставив неизменными массу m2 шарика и амплитуду А1 его колебаний измерьте период колебаний маятника для l2=75 см и запишите значения в таблицу 2.
2. Измените длину маятника l2=50 см и измерьте период его колебаний. Результат запишите в таблицу.
3. По результатам измерений сделайте вывод, зависит ли период малых колебаний маятника от его длины.
Контрольные вопросы
1. Какую длину должен иметь секундный математический маятник?
2. Вычислите, каким должен быть период колебаний маятника длиной l =64 см.
3. Определите экспериментально период колебаний маятника длиной l = 64 см и сравните с рассчитанным значением.
Можно показать, что для дискретных случайных величин при большом числе опытов среднее арифметическое наблюдаемых значений случайной величины приближается к ее математическому ожиданию.
Пусть производится N независимых опытов, в каждом из которых величина Х принимает определенное значение. Предположим, что значение х 1 появилось m 1 раз, значение х 2 появилось m 2 раза, вообще х i появилось m i раз. Очевидно,
S m i = N
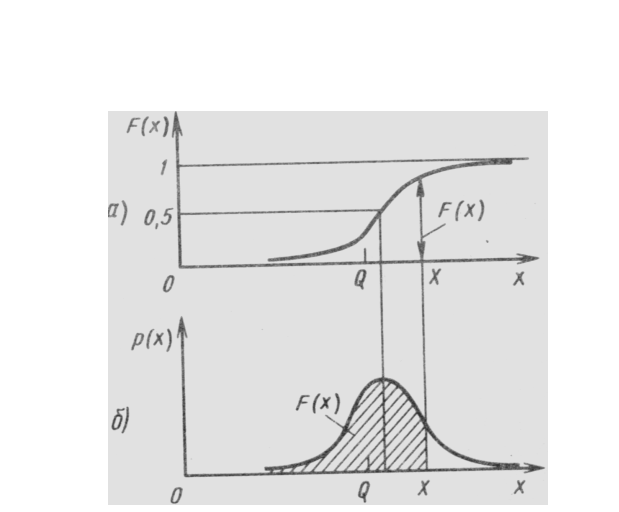
Рис. 2.1. Функции распределения:
а – интегральная, б – дифференциальная.
Вычислим среднее арифметическое наблюдаемых значений величины Х, которое в отличие от математического ожидания обозначим М * (Х) :
М * (Х) = S (х i m i ) / N = S х i ( m i / N) = S x i p i *, (2.2)
где р i*-частота или статистическая вероятность события. При увеличении числа опытов величины рi*будут приближаться (сходиться) к соответствующим вероятностям рi . Следовательно, и среднее арифметическое М *(Х) будет сходиться к математическому ожиданию М(Х), определяемому формулой (2.1).
Найдем математическое ожидание погрешности измерения:
МD = М (X – Q ) = ò (X – Q) p(X) dX = ò X p(X)dX - ò Q p(X) dX =
= MX - Q ò p(X) dX = MX – Q = Dm (2.3)
Интегрирование ведется от - ¥ до + ¥ .
Строго говоря, выражение (2.3) определяет систематическую погрешность измерений.
Случайная погрешность представляет собой разность между результатом однократного наблюдения и математическим ожиданием результатов: D i = X i – MX
Любая погрешность однократного наблюдения равняется сумме систематической и случайной погрешностей.
 Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания :
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания :

 DX = ò (X – MX) 2 p (X) dX (2.4)
DX = ò (X – MX) 2 p (X) dX (2.4)
n
Для дискретных величин DX = S (X k – MX) 2 p k (2.5)
k=1
Дисперсия является характеристикой рассеяния результатов измерений относительно математического ожидания. Но дисперсия неудобна для оценки рассеяния, так как имеет размерность квадрата случайной величины.
Поэтому для оценки рассеяния принимают среднее квадратическое отклонение, за которое принимают положительное значение корня квадратного из дисперсии и обозначают s Х :

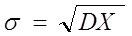 (2.6)Для исключения систематической погрешности вводят поправку, умножая величину дисперсии на n / (n-1) . Отсюда среднее квадратическое отклонение SX дискретной случайной величины X находят по формуле, имеющей широкое практическое применение:
(2.6)Для исключения систематической погрешности вводят поправку, умножая величину дисперсии на n / (n-1) . Отсюда среднее квадратическое отклонение SX дискретной случайной величины X находят по формуле, имеющей широкое практическое применение:


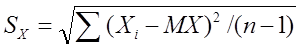 (2.7)
(2.7)
Лекция 3. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.
ПЛАН: 1. Нормальный закон распределения.
2. Другие законы распределения.
3. Идентификация законов распределения. Критерии согласия.
4 .Доверительный интервал и доверительная вероятность.
3.1.НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ.
Распределение вероятностей – одно из центральных понятий теории вероятностей и математической статистики. Определение распределения вероятностей равносильно заданию вероятностей всех случайных событий, описывающих некоторое случайное явление.
Одним из наиболее распространенных является нормальный закон распределения, что объясняется центральной предельной теоремой теории вероятностей: распределение случайных значений физической величины (так же, как и погрешностей измерения) будет близко к нормальному всякий раз, когда результаты измерений формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных факторов.
Нормальный закон имеет следующее выражение для дифференциальной функции (плотности) распределения:
р (Х) = 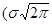 ) –1 exp { - ( X - MX) 2 / 2 s 2x } (3.1)
) –1 exp { - ( X - MX) 2 / 2 s 2x } (3.1)
Графически эта функция представлена на рис. 3.1 для различных значений дисперсии s ( s 1 < s 2).
Из уравнения (3.1) можно заключить:
1) Плотность вероятностей имеет максимум при Х = МХ ;
2) С увеличением погрешности D = Х – МХ независимо от знака (функция четная) плотность вероятности стремится к нулю;
3) С увеличением дисперсии вероятность больших отклонений увеличивается.
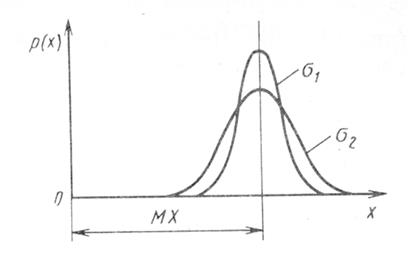
Рис. 3.1. Дифференциальные функции нормального распределения.
Нормальное распределение отлично от нуля на всей бесконечности оси Х, однако реальные физические величины обычно принимают определенные значения, лежащие в конечном интервале (а, в). Форма функции распределения нормальной случайной величины в пределах этого интервала:
+¥
F ( а < Х < в ) = ( 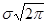 ) ò ехр {- (Х - МХ) 2/ 2 s Х2 } dX (3.2)
) ò ехр {- (Х - МХ) 2/ 2 s Х2 } dX (3.2)
_¥
Кривая нормального распределения изменяется в зависимости от дисперсии (рис. 3.1). Но если сделать замену переменных и ввести переменную
t = (X – MX) / s X , dX = s x dt ,получим кривую нормированного нормального распределения:
p (t) = ( 1 / 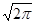 ) exp ( - t 2 / 2 )
) exp ( - t 2 / 2 )
Интеграл от правой части (2.10) не выражается через элементарные функции. Поэтому обычно пользуются таблицами функции Лапласа:
Z
Ф ( z ) = ( 1/ 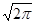 ) ò exp ( - t 2/ 2 ) d t (3.3)
) ò exp ( - t 2/ 2 ) d t (3.3)
- ¥
Ф ( - ¥ ) = 0 ; Ф ( + ¥ ) = 1 ; Ф ( - z ) = 1 – Ф ( z ).
В литературе функция Лапласа называется функцией погрешности или интегралом ошибок и обозначается « erf (z)».
3.2. ДРУГИЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ.
А) Равномерное распределение.
Если случайная величина может принимать любые значения, не выходящие за некоторые границы с одинаковой вероятностью, то распределение ее вероятностей описывается равномерным законом, При этом плотность вероятности р (D) постоянна внутри этих границ и равна нулю за их пределами (рис. 3.2-а). Аналитическая зависимость р (Х) описывается следующим образом:
р (Х) = 1 / (Х 2 – Х 1) при Х 1 < Х < Х 2 ;
р (Х) = 0 при Х < Х 1 и Х > Х 2 .
С таким законом распределения хорошо согласуются погрешности от трения в опорах электромеханических приборов, неисключенные остатки систематических погрешностей, погрешность дискретности в цифровых приборах и др.
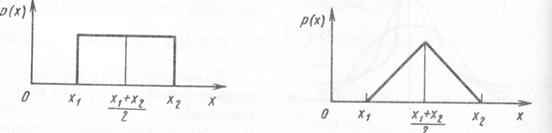
а) б )
Рис. 3.2. Дифференциальная функция
равномерного (а) и треугольного (б) распределений.
Б) Закон треугольного распределения (закон Симпсона).
Вид кривой треугольного распределения показан на рис. 3.2-б. По такому закону распределены погрешности суммы (разности) двух равномерно распределенных величин. Например, если отклонения размеров отверстия и вала распределены в пределах допусков равномерно, то зазоры в пределах допуска будут распределены по треугольному закону.
Треугольный закон распределения является разновидностью трапецеидального закона распределения. Погрешность имеет этот закон распределения, если она образуется из двух независимых составляющих, каждая из которых имеет равномерный закон распределения, но ширина интервала равномерных законов различна. например, при последовательном соединении двух измерительных преобразователей.
В) Закон Пуассона (экспоненциальный закон).
Рассмотрим дискретную случайную величину, которая может принимать только целые, неотрицательные значения: 0, 1, 2, … m,…, причем последовательность этих значений теоретически не ограничена.
Говорят, что случайная величина распределена по закону Пуассона, если вероятность того, что она примет определенное значение m, выражается формулой:
Рm = a m [ exp (- a)] / m ! , (3.4)
где а– некоторая положительная величина, называемая параметром закона Пуассона; m = 0, 1, 2, … .
Замечательным свойством закона Пуассона является то, что математическое ожидание и дисперсия распределения равны друг другу и его параметру: МХ = D = а. Это свойство часто используется на практике для идентификации закона распределения Пуассона
Закон Пуассона выражает распределение вероятностей случайных событий при большом числе опытов и малой вероятности отдельного события, поэтому его часто называют законом редких явлений.
Например, число осколков, попадающих в малоразмерную цель при заданном положении точки разрыва гранаты, распределяется по закону Пуассона.
3.3. ИДЕНТИФИКАЦИЯ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ.
Идентификация (определение) законов распределения производится экспериментально. Их знание очень важно, когда предъявляются высокие требования к достоверности результатов обработки эксперимента.
Для нахождения закона распределения той или иной величины необходимы сотни и тысячи измерений. По результатам эксперимента строят эмпирическое распределение полученных значений случайных физических величин или их погрешностей.
После построения эмпирического закона распределения необходимо построить модель теоретического распределения и проверить ее соответствие тому или иному закону распределения с помощью критериев согласия. Все эти процедуры проводятся методами математической статистики.
А) Выравнивание статистических рядов.
Результаты измерений физической величины, расположенные в определенном порядке, образуют статистический ряд. При обработке статистического материала часто приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую лишь существенные черты статистического материала, но не случайности, связанные с недостаточным объемом экспериментальных данных Такая задача называется задачей выравнивания (сглаживания) статистических рядов.
При сглаживании эмпирических зависимостей очень часто пользуются методом наименьших квадратов, считая, что наилучшим приближением к эмпирической зависимости является такое, при котором сумма квадратов отклонений обращается в минимум. При этом форма «сглаженной» кривой выбирается с учетом физического смысла измеряемой величины или зависимости, а затем определяются параметры теоретической зависимости (например, уравнения прямой, параболы и т.д.), обеспечивающие наилучшее приближение к эмпирической зависимости .
Метод наименьших квадратов теоретически обоснован тем, что при большом числе факторов, определяющих погрешность измерений, распределение вероятностей измеряемой величины в большинстве случаев является нормальным (3.2 ).
Б) Критерии согласия.
Допустим, что данное статистическое распределение выровнено с помощью некоторой теоретической кривой f (X). Как бы хорошо ни была подобрана теоретическая кривая, между нею и статистическим распределением неизбежны некоторые расхождения. Возникает вопрос :
Объясняются ли эти расхождения случайными обстоятельствами, связанными с ограниченным числом измерений, или они являются существенными и связаны с тем, что подобранная кривая плохо выравнивает данное статистическое распределение? Для ответа на этот вопрос существуют так называемые критерии согласия.
При помощи критериев согласия проверяют, удовлетворяет ли рассматриваемая случайная величина Х заданному закону распределения Fo (X). Наиболее распространенным из них является так называемый c 2 («хи квадрат») - критерий Пирсона.
Рассмотрим случай, когда распределение Fo (X) полностью определено, т.е. не содержит неизвестных параметров. Область эмпирических значений случайной величины делится на конечное число kнепересекающихся множеств (классов или разрядов): D Х 1 , …, D Х к . При непрерывном Х классы D Х i являются промежутками, при дискретном Х – группами возможных значений Х. Пусть р i есть «теоретическая вероятность того», что Х попадает в D Х i , если верна гипотеза о том, что
F X (X) = F o (X) (3.5)
. Если D Х i = (а, b ),то p i = Fo (b) – Fo (a).
Далее из Х производится выборка (X 1, … X n) объемаn. Пусть М i - число значений выборки, попадающих в интервал класса DХ i . Тогда
n n
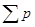 i = 1 ;
i = 1 ; 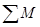 i = n .Число классов разбиения можно найти по формуле
i = n .Число классов разбиения можно найти по формуле
i=1 i=1 k = 3 lg n + 1 .
На практике рекомендуется иметь в каждом классе (разряде) не менее
5-10 результатов измерений.
При этих предположениях Пирсон предложил рассматривать распределение контрольной величины (квантиля):
K 2
c 2 = 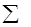 ( M i – np i ) 2 / np i = (
( M i – np i ) 2 / np i = ( 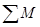 i / np i ) – n (3.6)
i / np i ) – n (3.6)
i = 1
Так как c 2 есть мера отклонения истинного распределения от гипотетического, то гипотеза (3.5) верна, если значение c 2, вычисленное по конкретной выборке согласно (3.6), меньше определенного критического значения ca2 для заданного уровня значимости a (или вероятности р) и m = k – 1 степеней свободы ( число степеней свободы равно разности между числом классов и числом независимых условий («связей»), наложенных на р i , например: 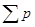 i = 1) . Если c 2 > c a2 , то гипотеза отвергается.
i = 1) . Если c 2 > c a2 , то гипотеза отвергается.
Для распределения c 2 составлены специальные таблицы. Следует отметить, что с помощью критериев согласия можно только опровергнуть гипотезу (3.5) или, наоборот, показать, что она не противоречит результатам опыта
Существуют и другие критерии согласия, например, критерий А.Н.Колмогорова, который в качестве меры расхождения между теоретическим и статистическим распределениями рассматривает максимальное значение модуля разности между статистической и теоретической функциями распределения. Этот критерий выгодно отличается от c 2 – критерия большей простотой.
2.3. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ И ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ.
В ряде задач требуется не только найти для параметра «а» распределения
подходящее численное значение, но и оценить его точность и надежность. Такие задачи особенно актуальны при малом числе измерений, когда статистическая («точечная») оценка параметра в значительной мере случайна и приближенная замена параметра а его оценкой а*может привести к серьезным ошибкам.
Для оценки ошибки такой замены назначим некоторую (достаточно большую: 0,9 или 0,99) вероятность bтого, что величина апопадет в интервал I b, или иначе говоря – того, что случайный интервал I b накроет точку а.Вероятность bпринято называть доверительной вероятностью, а интервал I b - доверительным интервалом. Границы интервала:
а 1 = (а * - e) и а 2 = (а * + e)называют доверительными границами.
Доверительный интервал можно еще рассматривать как интервал значений параметра а, совместимых с опытными данными и не противоречащих им.
Если известен закон распределения величины а *, то для нахождения доверительного интервала достаточно найти такое значение e ,для которого
Р ( êа* - а ê < e ) = b (3.7)
В случае нормального распределения случайной величины среднее квадратическое отклонение Sx =  s является 68 % - ным доверительным пределом.
s является 68 % - ным доверительным пределом.
Наибольшее распространение получила оценка погрешностей с помощью интервала 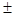 3 s(«шестисигмовый интервал»), для которого b = 0,9973.
3 s(«шестисигмовый интервал»), для которого b = 0,9973.
-
Дата добавления: 2015-02-10; просмотров: 2545;
