Термодинамика плавления двойной спирали (переходов спираль - клубок)

Рассмотрим простую двойную спираль, построенную из двух комплементарных гомополинуклеотидных цепей. В области перехода спираль-клубок такая молекула состоит из чередующихся спиральных и неупорядоченных участков — петель. Если обозначить число разорванных пар N₁, число связанных пар N₂ и число двуспиральных участков, равное числу петель, n, то свободная энергия системы запишется в виде:

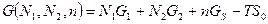
где G₁ и G₂ - свободные энергии полностью разделенных и полностью двуспиральных молекул, отнесенные к одной паре оснований, G_S - свободная энергия, необходимая для возникновения петли, т. е. расплавленной области между двумя спиральными. S₀ энтропия смешения спиральных и не спиральных участков, т. е. (в расчете на моль)

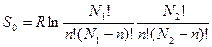
Минимум G при данной температуре соответствует условию

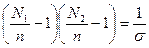
где 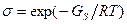есть фактор кооперативности. Чем меньше σ, тем больше кооперативность. Равновесные значения N₁ ,N₂ и n находятся путем дифференцирования G по N₁ , причем N₂ =N-N₁ , где N — константа. Приравняв ∂G/∂N₁ нулю, получаем:

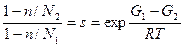
Таким образом, гомополимер в области перехода является последовательностью спиральных и не спиральных участков, размеры которых определяются σ. Это связано с одномерностью системы, которая, согласно теореме Ландау и Лившица, не может разделиться на фазы.

Кривая плавления, т. е. зависимость доли неупорядоченных пар 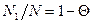(Θ- степень спиральности) от T, идет тем круче, чем меньше σ.

При σ=1 кооперативность отсутствует;

при σ =0 кооперативность полная. В середине интервала плавления модуль производной 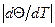максимален и интервал определяется условием

.

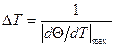Расчет, основанный на модели Изинга, дает:

,

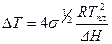где ΔH - разность энтальпий спиральной и не спиральной молекул в расчете на пару оснований. Из экспериментальных значений ΔT для синтетических гомополинуклеотидов получается σ~10^-4-10^-5, т.е. G_S≈30 кДж/моль. Степень кооперативности очень высока [4].

где g₁ и g₂ - свободные энергии лигандов соответственно в не спиральных и спиральных участках. Последний член содержит энтропию смешения полимера с лигандами. Условие минимума ∂G/∂n=0 такое же, как и в предыдущем случае, т.е. средняя длина спиральных участков при данном Θ не зависит от присутствия лигандов. С другой стороны, из условия ∂G/∂N₁=0 получается:

,

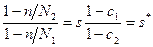где c₁=m₁/N₁, c₂=m₂/N₂. Эти концентрации лигандов выражаются через концентрацию лиганда в растворе c₀ и константы связывания K₁ и K₂

, .

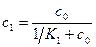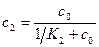Кривая плавления гомополиера без лигандов описывается функцией Θ=f(s), причем Θ=0,5 при s_пл=1, т.е. G₁=G₂. При наличии лигандов Θ=f(s^*) и Θ=0,5 при s^*, т.е. при

.

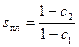Сдвиг температуры плавления по сравнению с таковой для чистого полимера T₀ определяется как

.

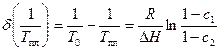Изменение интервала температур плавления есть

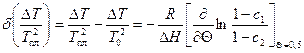
Полная концентрация лигандов в растворе и на полинуклеотиде равна

,

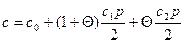где р - концентрация связывающих лиганды фосфатных групп полинуклеотида. Если с » р, то

, .

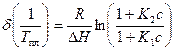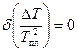При прочном связывании лигандов полимером во всей области перехода, т. е. при K₁p »1 или K₂p »1 и c ≈ p

,

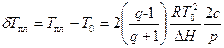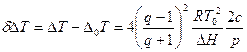
где q=K₂/K₁.

Такимобразом, лиганды действуют в качестве «скрепок», стабилизирующих двойную спираль [4].

Особенность гетерополимера состоит в относительно малом числе микросостояний, отвечающих данной энергии. Поэтому энтропия смешения не может существенно влиять на плавление. Вместе с тем появляется новый энергетический фактор, определяемый тем, что при уменьшении средней длины расплавленных участков содержание в них более стабильных пар GC должно уменьшаться. Конкуренция этого фактора и фактора, обусловленного невыгодностью «стыков» спиральных и не спиральных участков, должна приводить к чередованию спиральных и не спиральных участков определенной длины при данном значении Θ [4].

Приближенное решение задачи о плавлении гетерополимера с беспорядочной последовательностью пар получено Лазуркиным и Франк-Каменецким. Они разделили молекулу на одинаковые отрезки, каждый из которых содержит λ пар. Если λ достаточно велико, то распределение концентрации пар GC по этим отрезкам будет гауссовым, т. е.:

,

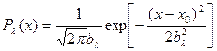где 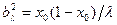, x- содержание пар GC, x₀- значение х, отвечающее максимуму распределения.

Общее число пар GC в расплавленных участках минимально, если все отрезки с содержанием этих пар, меньшим некоторого предельного значения x_λ расплавлены и все отрезки с x >x_λ спиральны. Значение x_λ определяется условием:

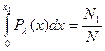
Средняя концентрация GC в расплавленных участках равна

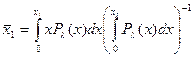
Так как состав каждого отрезка не зависит от состава других, вероятность того, что расплавленная область состоит из r отрезков, следующих друг за другом, равна

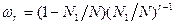
и среднее число отрезков расплавленной области

.

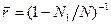Среднее число пар оснований в расплавленной области

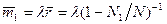
и число расплавленных областей во всей молекуле

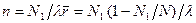
Свободная энергия полимера

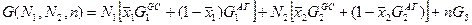
где G_S - энтропийный вклад, определяемый смешением областей. Вводя условия N₁+N₂ =N, <x₁>N₁+<x₂>N₂=x₀N, выражая n через λ, обозначая ΔG_GC=G₁^GC-G₂^GC, ΔG_AT=G₁^AT-G₂^AT и отбрасывая постоянные члены, получим

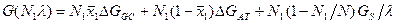
Равновесные значения N₁ и λ находятся из условия минимума выражения G(N₁,λ).

Интервал плавления гетерополимера

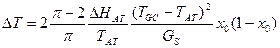
где T_GC и T_AT - температуры плавления для соответствующих полимеров. Средняя длина спиральной области:

.

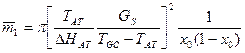Определения оптической плотности (и, следовательно, Θ) и размеров молекулы ДНК в растворе путем измерения характеристической вязкости в процессе плавления позволили найти средние длины спиральных участков: 1000-2500 пар при Θ=0,8-0,9 и 400-500 пар при Θ=0,5.

Ширина интервала плавления молекул ДНК со случайной последовательностью нуклеотидов составляет 2,5-3°С. ДНК бактерий - около 5°С, ДНК высших организмов - около 10°С, что свидетельствует об их блочном строении. Молекулярная масса блоков (5-15)·10⁹ [4].