НАРЕЗАНИЕ ЭВОЛЬВЕНТНЫХ ЗУБЬЕВ МЕТОДОМ ОБКАТКИ
Целью работы является ознакомление с нарезанием цилиндрических эвольвентных зубчатых колес инструментом реечного типа, изучение влияния смещения этого инструмента на форму и размеры нарезаемых зубьев.
8.1. Основные сведения из теории
Различают два метода нарезания зубьев цилиндрических эвольвентных зубчатых колес: метод копирования и метод обкатки.
При нарезании зубьев по методу копирования профиль зуба инструмента (пальцевые и дисковые фрезы, протяжки, долбежные головки, накатные ролики и т.п.) копирует профиль впадины между этими зубьями.
При нарезании по методу обкатки профиль зуба инструмента (зуборезные гребенки, червячные фрезы, долбяки, шеверы и т.п.) не копирует профиль указанной впадины. В процессе нарезания колеса данным методом колесу и инструменту сообщают такие движения друг относительно друга, при которых профиль зубьев колеса является огибающей последовательных положений режущих кромок инструмента.
Рассмотрим более подробно нарезание зубьев колеса методом обкатки зуборезной гребенкой, имеющей вид инструментальной зубчатой рейки и являющейся, как и, например, червячная фреза, инструментом реечного типа. В основу геометрии этого инструмента положен так называемый исходный контур цилиндрических эвольвентных зубчатых колес, определяемый ГОСТ 13755 – 81 и отображенный на рис. 8.1 сплошной линией. Прямая М – М, показанная на этом рисунке, называется делительной прямой. Она разделяет зубья контура на две части: головку и ножку. Высоты головки и ножки зубьев соответственно равны
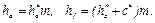
где m – модуль зубьев, 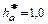 – коэффициент высоты головки зуба, с* = 0,25 – коэффициент радиального зазора.
– коэффициент высоты головки зуба, с* = 0,25 – коэффициент радиального зазора.
Шаг р зубьев контура и радиус 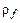 кривизны переходной кривой определяются выражениями:
кривизны переходной кривой определяются выражениями:
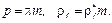
где 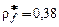 – коэффициент радиуса кривизны переходной кривой.
– коэффициент радиуса кривизны переходной кривой.
Контур рассматриваемой инструментальной зубчатой рейки отличается от охарактеризованного выше исходного контуpa лишь тем, что высота головок ее зубьев превышает высоту головок зубьев исходного контура на величину 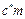 .
.

При нарезании колеса реечным инструментом по методу обкатки делительная окружность колеса перекатывается без скольжения по прямой инструментальной рейки, параллельной делительной прямой М –М этой рейки. Расстояние между делительной окружностью колеса и делительной прямой рейки М – М называется смещением инструмента. Величина смещения определяется произведением 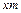 , где х – коэффициент смещения.
, где х – коэффициент смещения.
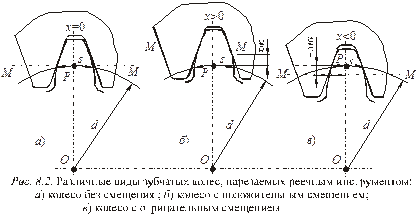
Если при нарезании колеса делительная прямая рейки М – М касается делительной окружности колеса (рис. 8.2,а), то х = 0 и нарезается колесо без смещения. Если рейка расположена относительно колеса так, что ее делительная прямая М – М не пересекается с делительной окружностью колеса и не касается ее, то х > 0 и колесо нарезается с положительным смещением (рис.8.2,б). Если же рейка расположена относительно колеса так, что делительная прямая рейки М – М пересекается с делительной окружностью колеса, то х < 0 и колесо нарезается с отрицательным смещением (рис. 8.2,в).
При изменении коэффициента смещения х изменяется форма и размеры зуба колеса. Так при х > 0 зуб имеет развитую ножку и малую толщину зуба по окружности вершин; при больших положительных смещениях возможно полное заострение зуба. При значительных отрицательных смещениях возможно подрезание зуба. При малом числе зубьев колеса подрезание возможно даже у колес, нарезаемых без смещения инструмента.
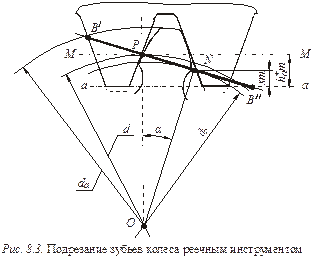
Причины возникновения подрезания зуба колеса иллюстрирует рис. 8.3, на котором изображено зацепление колеса с инструментальной зубчатой рейкой. Линия станочного зацепления начинается в точке N основной окружности колеса, проходит через полюс Р зацепления и уходит в бесконечность. Длина ее активной части ограничена точками В/ и В//, находящимися на пересечении этой прямой соответственно с окружностью вершин зубьев колеса и прямой а – а, отстоящей от делительной прямой М – М рейки на величину 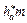 . Если точка В// будет находиться в пределах участка PN линии зацепления, то подрезания зуба колеса не будет. Если же эта точка будет располагаться вне данного участка, как это показано на рис. 8.3, то возникает подрезание зуба колеса, заключающееся в срезании переходной кривой и части эвольвентного профиля зуба в районе его ножки. Подрезание ослабляет ножку зуба колеса и может привести к уменьшению коэффициента перекрытия передачи.
. Если точка В// будет находиться в пределах участка PN линии зацепления, то подрезания зуба колеса не будет. Если же эта точка будет располагаться вне данного участка, как это показано на рис. 8.3, то возникает подрезание зуба колеса, заключающееся в срезании переходной кривой и части эвольвентного профиля зуба в районе его ножки. Подрезание ослабляет ножку зуба колеса и может привести к уменьшению коэффициента перекрытия передачи.
Наименьшее число зубьев колеса, нарезаемых без подрезания при отсутствии смещения реечного инструмента, определяется по формуле:
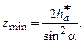 (8.1)
(8.1)
При стандартных значениях 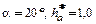 получаем
получаем  . Зубчатые колеса с числом зубьев
. Зубчатые колеса с числом зубьев 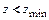 тоже могут быть нарезаны реечным инструментом без подрезания при условии положительного смещения инструмента относительно нарезаемого колеса (см. рис. 8.2,б) на величину, большую или равную
тоже могут быть нарезаны реечным инструментом без подрезания при условии положительного смещения инструмента относительно нарезаемого колеса (см. рис. 8.2,б) на величину, большую или равную 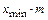 , где коэффициент наименьшего смещения вычисляется по формуле:
, где коэффициент наименьшего смещения вычисляется по формуле:
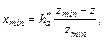 (8.2)
(8.2)
в которой z - число зубьев нарезаемого колеса.
Размеры зубчатого колеса определяются по приведенным ниже формулам.
1. Диаметры делительной и основной окружностей
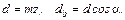 (8.3)
(8.3)
2. Шаг и толщина зуба по дуге делительной окружности
 (8.4)
(8.4)
3. Шаг и толщина зуба по дуге основной окружности
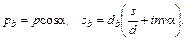 (8.5)
(8.5)
4. Диаметры окружностей впадин и вершин
 (8.6)
(8.6)
5. Толщина зуба по окружности вершин
 (8.7)
(8.7)
где 
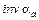 и
и 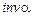
 – инволюты углов
– инволюты углов 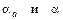
 , первый из которых определяется из выражения
, первый из которых определяется из выражения
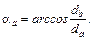 (8.8)
(8.8)
8.2. Описание прибора для профилирования зубьев колеса
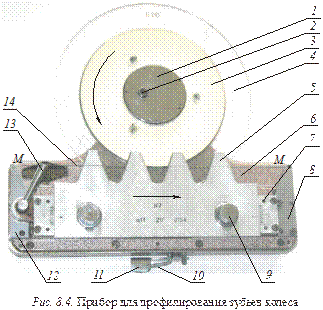
Лабораторная работа выполняется на специальном приборе (рис.8.4). Он позволяет методом обкатки построить такой профиль зуба колеса, который получается при данном положении инструментальной райки относительно заготовки колеса на зуборезном станке.
Рейка 5, размеры которой совпадают с размерами стандартной инструментальной рейки данного модуля, крепится на планке 6 винтами 9. По шкалам 7 рейка может быть установлена с нужным смещением относительно кромки М – М планки 6. Эта кромка совпадает с делительной прямой рейки при ее нормальном положении, когда риски на рейке находятся напротив цифры 0 на шкалах 7.
По кромке М – М планки 6 перекатывается диск 3, диаметр которого равен диаметру делительной окружности вычерчиваемого колеса. На рейке 5 указан диаметр этого диска, а также ее модуль и угол профиля. На диске 3 закреплен диск 4 большого диаметра, на котором с помощью прижимного устройства 1 и винтов 2 закрепляется бумага для вычерчивания зубьев. При завертывании винта 2 бумага накалывается на три острия.
Рейка может быть установлена со сдвигом до 10 мм oт нулевого положения. Чтобы избежать проскальзывания при перекатывании, диск 3 охвачен струной 14, один конец которой прикрепляется к неподвижному захвату 6, а второй конец – к захвату 12. Захват 12 при помощи эксцентрикового механизма, управляемого рукояткой 13, может несколько перемещаться и создавать необходимое натяжение струны 14.
Совместное движение рейки и диска осуществляется при помощи шагового храпового механизма, приводящегося в действие от рычага 11. При нажатии на рычаг 11 рейка подается налево (по стрелке) на 4-5 мм, при освобождении рычага 11 рейка фиксируется запирающей собачкой. Поворотом рычага 10 против хода часовой стрелки рейка получает возможность свободного перемещения от руки направо и налево.
8.3. Порядок выполнения работы
1. Ознакомиться с прибором (рис. 8.4и модель).
2. По указанным на рейке значениям модуля m и делительного диаметра нарезаемого колеса d определить число зубьев этого колеса, используя одну из формул выражения (8.3). -
3.Установить рейку 5 прибора в положение 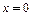 . При этом положении риски рейки находятся напротив цифры 0 на шкале 7. Передвинуть рейку в крайнее правое положение.
. При этом положении риски рейки находятся напротив цифры 0 на шкале 7. Передвинуть рейку в крайнее правое положение.
4. Нарезать (вычертить) три зуба колеса без смещения, для чего:
- установить на приборе бумажный диск - заготовку;
- остро заточенным карандашом очертить те зубья рейки, которые попадают на бумажный диск;
- нажать на рычаг 11, при этом рейка сдвинется влево на 4-5 мм, в этом положении вновь очертить все зубья райки, попадающие на бумажный диск, и так продолжать до тех пор, пока на заготовке полностью не сформируются тризуба.
5. Убедиться, что нарезанные зубья получились подрезанными, что и должно было произойти, так как число зубьев нарезаемого колеса z, подсчитанное при выполнении пункта 2 меньше, чем  при использовании стандартного инструмента.
при использовании стандартного инструмента.
6. По формуле (8.2) подсчитать величину коэффициента наименьшего смещения 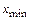 и смещения рейки
и смещения рейки 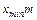 .
.
7. Нарезать (вычертить) тризуба колеса с рассчитанным смещением, для чего:
- установить рейку в положение, соответствующее положительному смещении 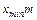 (рис 8.2,б);
(рис 8.2,б);
- передвинуть рейку в крайнее правое положение;
- установить напротив зубьев рейки чистую часть бумажного диска (заготовки), повернув его на 180° (для этого отвернув рычаг 13, повернуть диск 4 рукой без перемещения рейки, затем рычаг 13 завернуть до отказа), и вычертить три зуба со смещением, согласно пункта 4.
8. Рассчитать по формулам (8.3)–(8.8) геометрические параметры двух колес: одного без смещения, когда 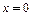 , и второго со смещением, когда
, и второго со смещением, когда 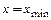 .
.
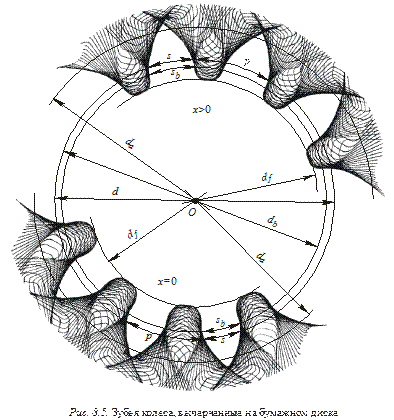
9. Снять заготовку с прибора, провести на чертеже основную и делительную окружности, окружности вершин и впадин для обоих колес. Вид вычерченных зубьев со всеми окружностями показан на рис. 8.5.
10. Измерить толщины зубьев 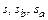 и сравнить их с расчетными.
и сравнить их с расчетными.
11. Оформить отчет и приложить к нему диск с вычерченными профилями зубьев.
8.3. Вопросы для самоконтроля
1. Какие существует методы нарезания зубьев? Охарактеризуйте каждый из них.
2. Изобразите исходный контур реечного инструмента и укажите его параметры.
3. Каково относительное движение колеса и зубчатой рейки в процессе нарезания?
4. Что такое смещение исходного контура и как различает смещение по знаку?
5. Когда наблюдается явление подрезания зуба колеса реечным инструментом? Выведите формулу для определения минимального числа зубьев колеса, нарезанных без подрезания при отсутствии смещения реечного инструмента.
6. Выведите формулу, позволяющую определить минимальное смещение реечного инструмента, обеспечивающее отсутствие подрезания зуба колеса.
7. Какие еще существуют методы устранения подрезания зубьев колеса?
8. Какие параметры зубчатого колеса изменяются при нарезании его со смещенным режущим инструментом? Какие параметры остаются постоянными?
9. Сформулируйте основную теорему зацепления.
10. Что такое шаг и модуль зубьев колеса? Выведите формулу для определения шага и толщины зубьев колеса по дуге окружности произвольного радиуса.
Дата добавления: 2015-02-07; просмотров: 4045;
