ГРАФИЧЕСКОЕ ИССЛЕДОВАНИЕ КИНЕМАТИКИ ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВ II КЛАССА
Целью работы является построение планов положений плоского рычажного механизма II класса и определение кинематических характеристик его звеньев.
2.1. Основные сведения из теории
Задачи кинематического исследования механизма заключаются в определении:
1) положений звеньев механизма в различные моменты времени;
2) траекторий некоторых точек звеньев;
3) величины и направления линейных скоростей и ускорений точек, угловых скоростей и угловых ускорений звеньев механизма.
 |
При кинематическом исследовании сложного механизма определение положений, скоростей и ускорений точек начинают с входного звена и непосредственно присоединенной к нему группы Ассура. Далее находят те же параметры точек других групп Асура, соблюдая последовательность рассмотрения данных групп, соответствующую формуле строения механизма.
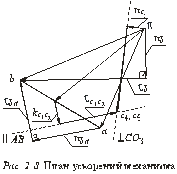
Положения звеньев механизма определяют в процессе построения его планов, каждый из которых представляет собой изображение кинематической схемы механизма в выбранном масштабе, соответствующее заданному положению ведущего звена. Решать задачу о положении звеньев механизма рекомендуется в следующей последовательности (рис. 2.1):
– строят план механизма в крайнем положении, при котором точки А и В занимают положение А0 и В0;
– разбивают траекторию точки А конца кривошипа на требуемое число равных частей, получая последовательные положения точки и кривошипа;
– строят план механизма для всех его положений методом засечек.
Траектории отдельных точек механизма определяют на основе его планов как геометрическое место этих точек при различных положениях ведущего звена.
Задачу, связанную с нахождением скоростей и ускорений точек механизма, решают с помощью планов скоростей и ускорений. Изложим особенности этого решения на примере конкретного механизма.
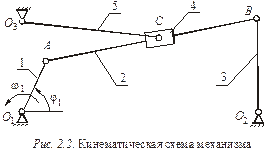
Дано: кинематическая схема механизма (рис. 2.2); длины звеньев 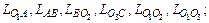 угловая скорость входного звена
угловая скорость входного звена 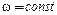 ; угловая координата входного звена
; угловая координата входного звена 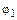 .
.
Определить: скорости и ускорения точек механизма, а также угловые скорости и ускорения звеньев в данный момент времени.
Решение
Для определения скоростей и ускорений точек механизма построим его план в масштабе KL, который вычислим по формуле
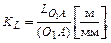 (2.1)
(2.1)
где 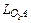 – истинное значение длины звена в метрах;
– истинное значение длины звена в метрах; 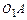 – длина отрезка, изображающего кривошип на чертеже в миллиметрах.
– длина отрезка, изображающего кривошип на чертеже в миллиметрах.
Абсолютная скорость точки А (её вектор 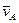 перпендикулярен
перпендикулярен 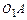 ) определяется из выражения:
) определяется из выражения:
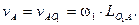 (2.2)
(2.2)
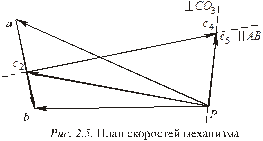
Построим план скоростей механизма. При построении этого плана обратим внимание на то, что лучи, выходящие из его полюса, изображают абсолютные скорости точек звеньев механизма, а отрезки, соединяющие концы этих лучей – относительные скорости данных точек. Полюс плана скоростей обозначим буквой «р». Для удобства план скоростей будем строить в масштабе условного кривошипа. Поэтому длину отрезка ра вектора скорости точки А кривошипа изобразим на плане скоростей (рис. 2.3) кратной длине кривошипа, отображенного на плане механизма. Длину ра определим из выражения 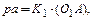 где К1 – масштаб условных кривошипов (любое число). Тогда масштаб плана скоростей вычислим по формуле:
где К1 – масштаб условных кривошипов (любое число). Тогда масштаб плана скоростей вычислим по формуле:
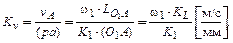 (2.3)
(2.3)
Для определения скорости точки В запишем векторное уравнение:
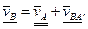 (2.4)
(2.4)
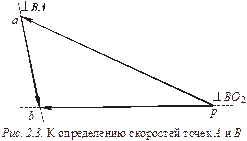
В уравнении (2.4) вектор 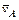 известен по величине и по направлению (подчеркнут двумя линиями), а векторы
известен по величине и по направлению (подчеркнут двумя линиями), а векторы 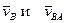 – только по направлению (подчеркнуты одной линией). Поэтому на плане скоростей можно показать только их направления. Так как вектор
– только по направлению (подчеркнуты одной линией). Поэтому на плане скоростей можно показать только их направления. Так как вектор 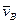 является абсолютной скоростью точки В третьего звена, то его направление следует проводить из полюса, а направление вектора
является абсолютной скоростью точки В третьего звена, то его направление следует проводить из полюса, а направление вектора 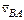 – из точки «а» плана скоростей.
– из точки «а» плана скоростей.
Точка пересечения двух указанных направлений определит искомые величины векторов:
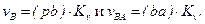
Тогда
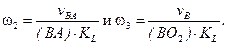 (2.5)
(2.5)
Скорость тоски С2, принадлежащей второму звену, определим из уравнения:
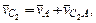 (2.6)
(2.6)
где 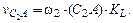
Анализируя уравнения (2.5) и (2.6) получим:
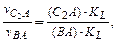
или через отрезки планов скоростей механизма
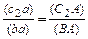 .
.
(2.7)
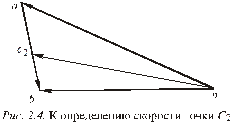
Абсолютную скорость точки С2 (рис. 2.2) определим по формуле: 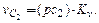
Из схемы механизма видно, что ползун 4 находится в сложном движении, поэтому абсолютная скорость точки С4 определяется векторным равенством:
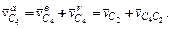 (2.8)
(2.8)
Так как звенья 4 и 5 соединены шарнирно, то 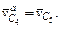 Тогда
Тогда 
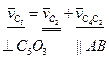 . (2.9)
. (2.9)
Заканчиваем построение плана скоростей, и из него находим
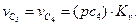
Тогда угловая скорость 5 звена
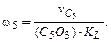 (2.10)
(2.10)
Построим план ускорений. Особенности его построения такие же, как и особенности построения плана скоростей. Полюс плана ускорений обозначим буквой «π».
Абсолютное ускорение точки А можно представить векторным равенством
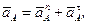 (2.11)
(2.11)
Так как ω1=const, то 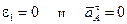 . Поэтому вектор
. Поэтому вектор 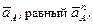 направлен параллельно звену 1 к центру вращения О1 и по величине равен:
направлен параллельно звену 1 к центру вращения О1 и по величине равен:
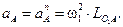
План ускорений строим в масштабе условных кривошипов К2. Для этого вектор 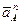 откладываем на плане ускорений в виде отрезка
откладываем на плане ускорений в виде отрезка 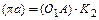 , кратного длине кривошипа О1А на плане механизма (рис. 2.2). Тогда масштаб плана ускорений можно найти по формуле:
, кратного длине кривошипа О1А на плане механизма (рис. 2.2). Тогда масштаб плана ускорений можно найти по формуле:
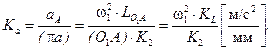 (2.12)
(2.12)
Для определения ускорения точки В можно записать уравнения:
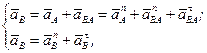 или
или
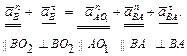 (2.13)
(2.13)
В уравнении (2.13), как и в уравнении (2.4), векторы, известные по величине и направлению, подчеркнуты двумя линиями, а векторы, известные только по направлению, – одной линией. В этом уравнении
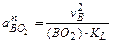 и направлено от точки В к точке О2;
и направлено от точки В к точке О2; 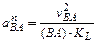 и направлено от точки В к точке А;
и направлено от точки В к точке А; 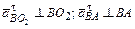 – неизвестны по величине, так как неизвестны угловые ускорения
– неизвестны по величине, так как неизвестны угловые ускорения 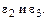
Длины отрезков, изображающих на плане ускорений векторы 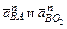 , определяются из выражений:
, определяются из выражений:
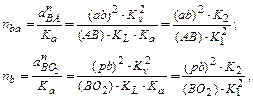
где (ab) и (pb) – отрезки на плане скоростей.
Построим план ускорений, используя уравнение (2.13). Из полюса π откладываем отрезок (πа) (рис. 2.6), изображающий в масштабе условных кривошипов К2 ускорение 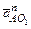 .
.
Затем из конца этого вектора проводим отрезок nba, а из конца последнего – прямую по направлению вектора тангенциального ускорения 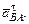 Далее из полюса π откладываем отрезок nb и из конца этого отрезка проводим прямую по направлению тангенциального ускорения
Далее из полюса π откладываем отрезок nb и из конца этого отрезка проводим прямую по направлению тангенциального ускорения 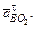
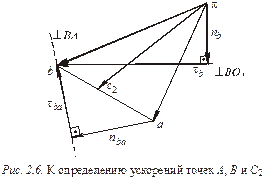
Пересечение двух прямых известных направлений векторов в точке b определит их искомые величины. Тогда:
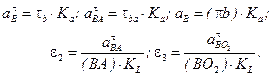 (2.14)
(2.14)
Ускорение точки С2 можно определить, решив уравнение:
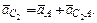 (2.15)
(2.15)
Модуль ускорения 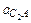 можно найти из соотношения:
можно найти из соотношения:
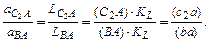
Тогда по рис. 2.6: 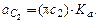
Перейдем к определению ускорений точек С4 и С5. Ускорение точки С4 можно найти, решив векторное уравнение:
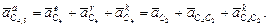 (2.16)
(2.16)
Величина ускорения Кориолиса определяется по формуле:
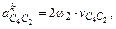
где ω2 – угловая скорость переносного движения;
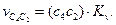
Согласно известному правилу, определим направление ускорения Кориолиса (рис. 2.7):

Отрезок 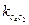 , изображающий на плане ускорений вектор
, изображающий на плане ускорений вектор 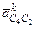 , можно вычислить по формуле:
, можно вычислить по формуле:
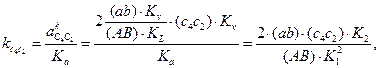
где (ab) и ( 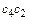 ) – отрезки плана скоростей.
) – отрезки плана скоростей.
Относительное ускорение 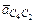 || АВ.
|| АВ.
Для определения ускорения точки С5 составим векторное уравнение:
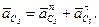 (2.17)
(2.17)
В этом уравнении 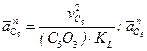 || С5О3 – направлено от точки С к точке О3;
|| С5О3 – направлено от точки С к точке О3; 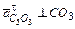 – неизвестно по величине, так как неизвестно
– неизвестно по величине, так как неизвестно 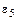 . Отрезок
. Отрезок 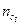 , изображающий на плане ускорений
, изображающий на плане ускорений 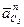 можно вычислить по формуле:
можно вычислить по формуле:
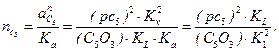
Так как точки С4 и С5 совпадают, то 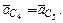 Тогда, приравняв правые части векторных уравнений (2.16) и (2.17), можно записать:
Тогда, приравняв правые части векторных уравнений (2.16) и (2.17), можно записать:
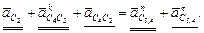 (2.18)
(2.18)
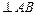 || АВ || СО3
|| АВ || СО3 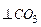
Заканчиваем построение плана ускорений (рис. 2.8). Для этого из точки с2 проведем отрезок 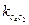 , а из его конца прямую по направлению вектора
, а из его конца прямую по направлению вектора 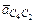 . Отрезок
. Отрезок 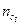 проведем из полюса π, а из конца этого отрезка – прямую по направлению вектора
проведем из полюса π, а из конца этого отрезка – прямую по направлению вектора 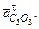 Пересечение двух прямых в точке С4 (С5) определит следующие искомые величины:
Пересечение двух прямых в точке С4 (С5) определит следующие искомые величины:
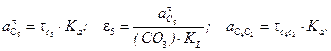 (2.19)
(2.19)
2.2. Порядок выполнения лабораторной работы
1. Определить размеры звеньев механизма, необходимые для вычерчивания планов.
2. Вычертить кинематическую схему механизма в крайнем положении в удобном масштабе. Определить масштаб длин по формуле:
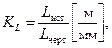
где 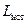 – истинное значение длины звена, м;
– истинное значение длины звена, м; 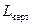 – длина отрезка, изображающего звено на чертеже, мм.
– длина отрезка, изображающего звено на чертеже, мм.
3. Звенья механизма пронумеровать арабскими цифрами, начиная с кривошипа. Шарниры обозначить заглавными буквами латинского алфавита А, В, С… При этом шарниры с неподвижными осями обозначить через О1, О2 … Отметить стрелкой направление вращения ведущего звена.
4. Произвести разметку траекторий точек механизма. Для этого траекторию точки А ведущего звена 1 разделить на произвольное число равных частей (например на 8). Методом засечек разметить траекторию точек звеньев.
5. Построить планы скоростей механизма для двух его положений (одно крайнее и одно промежуточное) в условном масштабе кривошипа К1. Подсчитать масштаб планов скоростей по формуле (2.3). Частоту вращения ведущего вала считать постоянной и равной 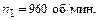
6. Построить планы ускорений механизма для тех же положений в условном масштабе кривошипа К2. Подсчитать масштаб планов ускорений по формуле (2.12).
7. Для одного из положений механизма (по заданию преподавателя) определить угловые скорости и ускорения всех звеньев по величине и направлению. Направления показать стрелками на плане механизма.
8. Оформить отчет.
2.3. Вопросы для самоконтроля
1. Что называется планом механизма?
2. Что называется масштабом?
3. Как построить механизм в крайнем положении выходного звена?
4. Как построить траекторию заданной точки механизма?
5. Что называется планом скоростей и ускорений?
6. Какое движение звена называется плоскопараллельным, а какое – сложным?
7.Сформулируйте теорему о сложении скоростей и ускорений для плоскопараллельного и сложного движения звена.
8. Как направлены нормальное и касательное ускорения точек звена при его вращательном движении?
9. Как определить величину и направление ускорения Кориолиса?
10. Как, пользуясь теоремой подобия, определить величину и направление скорости и ускорения третьей точки звена, если известны скорости и ускорения двух других его точек?
11. Как, пользуясь планами скоростей и ускорений, определить угловую скорость и угловое ускорение звена?
12. Постройте планы скоростей и ускорений для шарнирного четырехзвенника, кривошипно-ползунного и кулисного механизмов.
 3. АНАЛИТИЧЕСКОЕ И ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК МОДЕЛИ МАШИНЫ С ИСПОЛНИТЕЛЬНЫМ
3. АНАЛИТИЧЕСКОЕ И ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК МОДЕЛИ МАШИНЫ С ИСПОЛНИТЕЛЬНЫМ
КРИВОШИПНО-ПОЛЗУННЫМ МЕХАНИЗМОМ
На лабораторном стенде, являющемся физической моделью простейшей машины с кривошипно-ползунным исполнительным механизмом при заданных размерах его звеньев, провести кинематическое исследование его характеристик.
Для этого необходимо:
1. На базе кинематической схемы кривошипно-ползунного механизма и его математической модели провести аналитический анализ кинематических характеристик модели.
2. Ознакомиться с устройством стенда и порядком работы на нем.
3. Ознакомиться с устройством датчиков перемещения и скоростей, с принципами их работы.
4. Научиться обрабатывать экспериментально полученные осциллограммы.
5. Оценить результаты аналитического и экспериментального исследования.
3.1. Краткое описание стенда
Лабораторный стенд (рис. 3.1) представляет собой физическую модель машины с исполнительным кривошипно-ползунным механизмом. Изменение геометрических параметров механизма в сочетании с двухступенчатым редуктором позволяет получить довольно широкий диапазон для экспериментального и теоретического исследований кинематических характеристик стенда.
Стенд состоит из следующих составных частей и механизмов: стойки (основания) 13, на которой собран стенд; двигателя 12 с частотой вращения 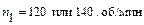 ; двухступенчатого редуктора 11; кривошипного механизма (детали 1, 2, 3, 4, 5); реостатных датчиков для измерения перемещений 6 и индукционных датчиков скоростей 7; тормоза 8; элементов управления.
; двухступенчатого редуктора 11; кривошипного механизма (детали 1, 2, 3, 4, 5); реостатных датчиков для измерения перемещений 6 и индукционных датчиков скоростей 7; тормоза 8; элементов управления.
Диск 1, являющийся кривошипом исполнительного механизма, имеет пять резьбовых отверстий, удаленных от центра вращения на различные расстояния l1 (50, 60,70, 80 и 90 мм). Они служат для соединения с шатуном 2, который также может иметь различную длину l2 (225, 275 и 285 мм). Ползун 3 движется в направляющих 4. Положение шарнира В на ползуне обеспечивается пластиной 5, перемещающейся на ползуне, на требуемую величину эксцентриситета е в пределах 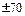 мм от оси вращения кривошипа. В нижней части ползуна закреплен поводок, связанный с датчиками 6 и 7, которые закрепляются на основании стенда 13.
мм от оси вращения кривошипа. В нижней части ползуна закреплен поводок, связанный с датчиками 6 и 7, которые закрепляются на основании стенда 13.
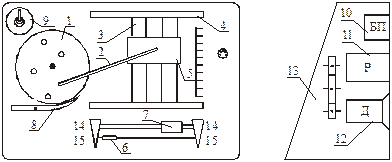
Рис. 3.1. Лабораторный стенд
1 – диск кривошипа, 2 – шатун, 3 – ползун, 4 – направляющие ползуна, 5 – пластина ползуна, 6 – датчик перемещения, 7 – датчик скорости, 8 – тормоз, 9 – выключатель, 10 – блок питания датчиков, 11 – коробка скоростей, 12 – электродвигатель, 13 – стойка (основание) стенда
В левом верхнем углу основания находится тумблер 9, с помощью которого включается и выключается стенд. Вверху справа расположен штекерный разъем для подключения регистрирующего прибора – шестиканального самописца Н 3. 38 – 6П.
На данном стенде кинематические характеристики, определяемые экспериментально, зависят от условий трения, зазоров в кинематических парах, упругости звеньев и определяются возможностями самого стенда.
Значительно расширить пределы измерения геометрических параметров модели и ее кинематических характеристик позволяет математическое моделирование, основанное на аналитическом исследовании механизмов.
3.2. Аналитическое исследование
Кинематическая схема исполнительного механизма представлена на рис. 3.2, где l1, l2 – длина кривошипа и шатуна соответственно, е – смещение пластины ползуна 5 относительно оси вращения кривошипа.
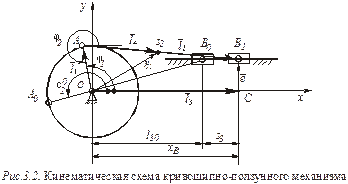
Для определения кинематических характеристик данного механизма используется метод замкнутых контуров, разработанный Зиновьевым В.А. [2].
Условие замкнутости контура ОАВС в векторном виде можно записать в виде:
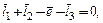 или
или 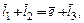 (3.1)
(3.1)
где 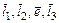 – векторы, изображающие стороны этого многоугольника.
– векторы, изображающие стороны этого многоугольника.
Векторное уравнение (3.1) эквивалентно двум скалярным, полученным проецированием обеих частей уравнения (3.1) соответственно на оси ox и oy:
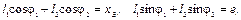 (3.2)
(3.2)
где φ1 и φ2 – углы, характеризующие положение соответственно кривошипа 1 и шатуна 2, отсчитываются от положительного направления оси ox в направлении вращения кривошипа.
Для данной схемы механизма с одной степенью свободы угол φ1 однозначно определяет положение шатуна и кривошипа и является обобщенной координатой. Таким образом, система уравнений (3.2) представляет математическую модель кривошипно-ползунного механизма стенда.
Из второго уравнения системы (3.2) следует, что
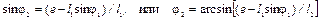 . (3.3)
. (3.3)
Первое уравнение системы (3.2), зависящее только от геометрии звеньев и обобщенной координаты φ1, является функцией положения ползуна кривошипно-ползунного механизма.
Первая производная от функции положения ползуна по обобщенной координате называется передаточной функцией или аналогом линейной или угловой скорости и обозначается соответственно 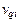 или
или 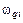 :
:
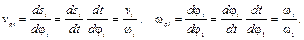 (3.4)
(3.4)
Отсюда следует, что действительные угловые и линейные скорости равны:
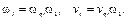 (3.5)
(3.5)
Вторая производная от функции положения по обобщенной координате называется передаточной функцией второго приближения или аналогом углового или линейного ускорения и обозначается соответственно 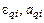 :
:
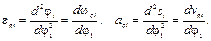
С учетом изложенного действительное угловое ускорение звена запишется в виде
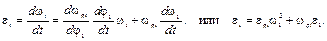 (3.6)
(3.6)
Если ω1 = const, то ε1 = 0. Тогда 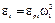 или
или 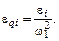
Таким образом, передаточные функции зависят от положения входного (начального) звена, в нашем примере кривошипа 1, размеров звеньев и могут быть определены без знания действительного закона движения входного звена.
Для определения передаточной функции скорости ползуна 
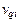 необходимо продифференцировать систему уравнений (3.2) по обобщенной координате φ1. После дифференцирования получим
необходимо продифференцировать систему уравнений (3.2) по обобщенной координате φ1. После дифференцирования получим
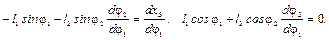 (3.7)
(3.7)
Совместное решение уравнений (3.7) с учетом (3.4) дает следующие выражения для передаточных функций скорости ползуна 3 и угловой скорости шатуна 2:
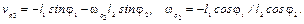 (3.8)
(3.8)
Для любой другой точки звеньев механизмов уравнения типа (3.1) и (3.2) составляются аналогично.
Например, для точки s2 на рис. 3.2, являющейся центром масс шатуна, векторное уравнение замкнутости многоугольника OAS2O имеет вид:
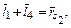
где 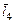 – вектор, определяющий положение точки s2 относительно шарнира А;
– вектор, определяющий положение точки s2 относительно шарнира А; 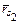 – радиус-вектор точки s2.
– радиус-вектор точки s2.
После проецирования этого уравнения на оси Ox и Oy получим соответственно выражения:
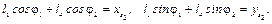
Продифференцировав эти уравнения по обобщенной координате φ1, получим
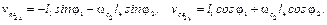 (3.9)
(3.9)
Полное значение передаточной функции скорости центра масс шатуна определяется формулой:
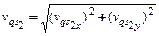 , (3.10)
, (3.10)
а скорость центра масс s2
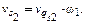 (3.11)
(3.11)
Передаточную функцию ускорений центра масс шатуна и ползуна повторным дифференцированием уравнений (3.7) и (3.9) рекомендуется получить самостоятельно, опираясь на изложенное выше.
Полагая ω1 = const , ускорение центра масс шатуна можно определить по формуле:
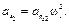 (3.12)
(3.12)
3.3. Экспериментальное определение кинематических характеристик кривошипно-ползунного механизма
3.3.1. Датчики для измерения перемещений и скоростей
Определение кинематических параметров машин при экспериментальном исследовании удобнее производить путем преобразования их в электрические величины, которые более точно регистрируются различными электронными приборами: осциллографами, самописцами и т. д. Эти приборы могут находиться на значительном расстоянии от объекта исследования, а их показания можно непосредственно ввести в память ЭВМ.
При выполнении настоящей работы на стенде используются реохордный датчик перемещений и индукционный датчик скоростей.
Датчик перемещений представляет из себя сопротивление в виде нихромной проволоки, которую называют реохордом. Основой датчика является измерительный мост сопротивления постоянного тока, в который включается сам реохорд, соединенный с подвижным контактом ползуна.
Подбирая сопротивление плеч моста и напряжение, можно получить наиболее удобный для последующей обработки записи вид кривой.
При передвижении подвижного контакта ползуна мост разбалансируется, а возникающее при этом напряжение на выходе будет пропорционально изменению сопротивления реохорда, то есть пропорционально перемещению.
Датчик измерения скорости состоит из двух неподвижных катушек, создающих постоянное магнитное поле, криволинейного стержня (магнитопровода) и подвижной катушки, которая соединена с ползуном. Метод измерения скорости основан на явлении электромагнитной индукции: при движении проводника в постоянном магнитном поле в нем индуцируется ЭДС, пропорциональная скорости движения проводника:
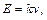
где k – коэффициент прибора, зависящий от величины магнитной индукции, длины проводника и других параметров.
Оба датчика подключаются к блоку питания, а сигналы с них подаются на вход усилителя записывающего прибора – самописца.
3.3.2. Обработка диаграмм
При экспериментальном определении кинематических характеристик на самописце получаются графики (рис. 3.3), отражающие зависимость
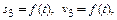
где s3 – перемещение ползуна 3, измеряемое от нулевого положения; v3 – скорость ползуна 3.
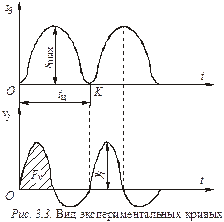
Отрезок ОК в масштабе kt, изображает время одного цикла (периода) машины. Тогда масштабный коэффициент может быть определен по формуле:
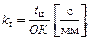 (3.13)
(3.13)
где tц – время одного цикла машины, которое через заданную частоту вращения кривошипа n1 [об/мин] или ω1 [рад/с] вычисляется соответственно следующим образом:
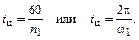 (3.14)
(3.14)
Масштабный коэффициент ks перемещения ползуна 3 вычисляется по формуле:
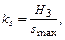 (3.15)
(3.15)
где Н3 – ход ползуна 3 (измеряется на экспериментальной установке), м; smax – максимальная ордината на графике 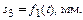
Так как график 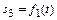
 можно получить, интегрируя график
можно получить, интегрируя график 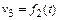 , то каждая ордината его, например smax, равна площади Fv графика v3 от начала цикла до точки, соответствующей ординате smax (на рис. 3.4 эта площадь заштрихована). В истинных единицах это равенство выглядит следующим образом:
, то каждая ордината его, например smax, равна площади Fv графика v3 от начала цикла до точки, соответствующей ординате smax (на рис. 3.4 эта площадь заштрихована). В истинных единицах это равенство выглядит следующим образом:
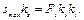 (3.16)
(3.16)
С учетом того, что левая часть уравнения (3.16) представляет собой ход ползуна Н3, масштабный коэффициент графика скорости kv может быть вычислен по формуле:
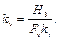 (3.17)
(3.17)
Площадь Fv можно измерить с помощью планиметра, а при его отсутствии – с помощью миллиметровки.
Зная масштабный коэффициент kv и имея график 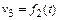 , для любого положения скорость ползуна может быть определена как произведение ординаты уi на коэффициент kv, то есть
, для любого положения скорость ползуна может быть определена как произведение ординаты уi на коэффициент kv, то есть
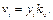 (3.18)
(3.18)
3.4. Порядок выполнения работы и оформления отчета
Расчет кинематических характеристик для заданного положения
1. Ознакомиться с экспериментальной установкой, отметить направление вращения кривошипа (по ходу или против хода часовой стрелки), вычислить угловую скорость кривошипа ω1 по данным своего варианта.
2. Вычертить в масштабе 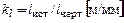 кинематическую схему кривошипно-ползунного механизма в двух крайних положениях. Крайними называются такие положения, в которых выходное звено меняет направление своего движения. Для кривошипно-ползунного механизма такими положениями являются те, в которых кривошип и шатун располагаются на прямой линии. За начальное положение механизма примем то, которое соответствует крайнему левому положению ползуна.
кинематическую схему кривошипно-ползунного механизма в двух крайних положениях. Крайними называются такие положения, в которых выходное звено меняет направление своего движения. Для кривошипно-ползунного механизма такими положениями являются те, в которых кривошип и шатун располагаются на прямой линии. За начальное положение механизма примем то, которое соответствует крайнему левому положению ползуна.
3. Провести на схеме оси неподвижной системы координат таким образом, чтобы начало координат располагалось в центре вращения кривошипа, положительное направление оси Ох – горизонтально в направлении движения ползуна, положительное направление оси Oy получается поворотом оси Ох на 90º в направлении движения кривошипа.
4. Обобщенную координату 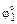 ,соответствующую начальному крайнему положению кривошипа, определить по формуле:
,соответствующую начальному крайнему положению кривошипа, определить по формуле:
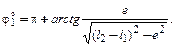
Примечание. Если в кривошипно-ползунном механизме направляющая, по которой движется ползун, расположена ниже оси Ох, а не выше, как показано на рис. 3.2, то в приведенной формуле и во всех остальных значение эксцентриситета е подставляется со знаком «–».
5. Для расчетного положения, указанного в варианте задания, вычислить величины: 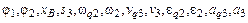 , используя формулы раздела 3.3, а также формулы, выведенные самостоятельно для определения передаточных функций углового и линейного ускорений.
, используя формулы раздела 3.3, а также формулы, выведенные самостоятельно для определения передаточных функций углового и линейного ускорений.
При этом перемещение ползуна s3 вычислить от начального крайнего положения, для чего можно воспользоваться формулой:
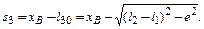
Примечание. Номер положения определяет значение обобщенной координаты φ1. Например, для положения 1:
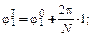
для положения 2:
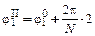
и так далее, где N – число расчетных точек (N = 8).
6. Изобразить на схеме, где вычерчены крайние положения, и расчетное положение механизма.
Экспериментальное определение кинематических характеристик ползуна
1. Изучить устройство установки, электрических датчиков и самописца.
2. Установить, согласно заданному варианту, скорость вращения кривошипа (таблица 3.1), для чего перевести рычаг переключения редуктора в положение I или II.
3. Установить, согласно заданию, размеры кривошипа, шатуна и смещение ползуна, после чего тщательно проверить крепление соединений.
4. Повернув диск кривошипа на 2…3 оборота, измерить масштабной линейкой ход ползуна Н3 [м].
5. Подключить датчики к самописцу с помощью соединительного шнура, и повернув диск кривошипа на 2…3 оборота, убедиться в наличии сигналов.
6. Установить скорость протяжки бумаги на самописце и величину усилия для получения удобного вида записей.
7. Включить установку, произвести запись перемещений и скоростей ползуна.
8. Выключить установку, снять полученные диаграммы, вклеить их в отчет.
9. Вычислить все масштабы, согласно формулам раздела 3.3.
10. Для расчетного положения найти точки на экспериментальных диаграммах и вычислить значения перемещений и скоростей ползуна.
3.5. Вопросы для самоконтроля
1. Какие части входят в состав экспериментальной установки?
2. В чем заключается суть аналитического исследования кинематики рычажного механизма, применяемого в данной работе?
3. Каково понятие функции положения звена механизма?
4. Что обозначают понятия передаточной функции линейной или угловой скорости?
5. Каково понятие функции линейного или углового ускорения?
6. Как определить масштаб перемещений?
7. Как определить масштаб скоростей?
8. Как определить масштаб времени?
9. Каков принцип работы датчика перемещений?
10. Каков принцип работы датчика измерений линейных скоростей?
Таблица 3.1
Варианты заданий
| Номер варианта | Частота вращения кривошипа n1, об/мин | Длина кривошипа l1, мм | Длина шатуна l2, мм | Эксцен- триситет е, мм | Номер расчетного положения |
| – 50 | |||||
| – 40 | |||||
| – 30 | |||||
| – 20 | |||||
| – 10 | |||||
| – 45 | |||||
| – 35 | |||||
| – 25 | |||||
| – 15 | |||||
| – 5 | |||||
| – 50 | |||||
| – 40 |
4. СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
Целью настоящей работы является построение профиля кулачка кулачкового механизма по заданному закону изменения аналога ускорения толкателя.
4.1. Общие сведения об углах кулачка кулачкового механизма.
Кулачковым называется механизм, в состав которого входит кулачок. Кулачок – звено высшей кинематической пары, имеющее переменную кривизну профиля и сообщающее толкателю движение, закон которого определяется этим профилем.
Основными параметрами, характеризующими геометрию кулачка, циклограмму работы кулачкового механизма и условия силового взаимодействия его звеньев, являются профильные и фазовые углы кулачка, а также углы давления и передачи движения.
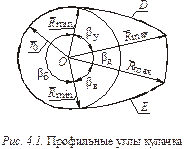 Представление о профильных углах можно получить с помощью радиуса-вектора его профиля
Представление о профильных углах можно получить с помощью радиуса-вектора его профиля 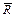 , который определяет положение текущей точки профиля относительно оси О вращения кулачка. Очевидно, что
, который определяет положение текущей точки профиля относительно оси О вращения кулачка. Очевидно, что 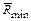 равен минимальному радиусу
равен минимальному радиусу 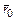 кулачка (рис. 4.1).
кулачка (рис. 4.1).
Угол βу –профильный угол удаления кулачка между минимальным 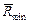 и максимальным
и максимальным 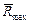 радиусами кулачка. Угол βв – профильный угол возвращения между максимальным
радиусами кулачка. Угол βв – профильный угол возвращения между максимальным 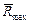 и минимальным
и минимальным 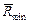 радиусами кулачка. Углы βу и βв ограничивают участки профиля кулачка переменной кривизны. Угол βд (βб) – профильные углы дальнего и ближнего стояния кулачка. Они охватывают дугу с постоянными максимальным и минимальным радиусами кулачка. Углы β не зависят от вида и расположения толкателя. Они показывают геометрию кулачка.
радиусами кулачка. Углы βу и βв ограничивают участки профиля кулачка переменной кривизны. Угол βд (βб) – профильные углы дальнего и ближнего стояния кулачка. Они охватывают дугу с постоянными максимальным и минимальным радиусами кулачка. Углы β не зависят от вида и расположения толкателя. Они показывают геометрию кулачка.
Указанным профильным углам соответствуют одноименные фазовые углы кулачка. Фазовые углы удаления φу и возвращения φв – уголы поворота кулачка за время максимального удаления и возвращения толкателя от оси кулачка. На фазовых углах φд , φб толкатель не подвижен. Фазовые углы зависят от вида и положения толкателя, и влияют на кинематические и динамические характеристики.
В общем случае одноименные фазовые и профильные углы не совпадают. Покажем это на примере кулачкового механизма с нецентральным поступательно движущимся заостренным толкателем (рис.4.2).
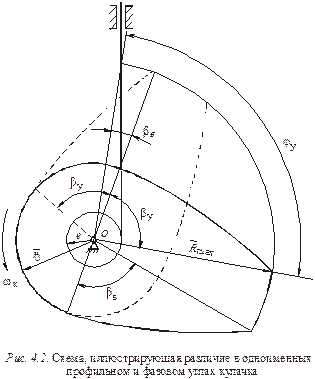
Изобразим кулачок в положении начала подъема толкателя. Повернем затем кулачок на угол βу (соответствующее положение кулачка показано пунктиром). Как видно на рис. 4.2, толкатель не занимает крайнее верхнее положение. Для того, чтобы он занял это положение нужно довернуть его на угол βе. Поэтому 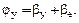
Аналогично можно показать, что 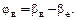 Если эксцентриситет толкателя е = 0, то βе= 0.
Если эксцентриситет толкателя е = 0, то βе= 0.
Для нахождения фазовых углов кулачка удобно пользоваться методом обращения движения, который заключается в том, что кулачковому механизму мысленно сообщается вращательное движение вокруг оси кулачка с угловой скоростью, равной по величине и противоположной по направлению угловой скорости ωк кулачка. Тогда кулачок становится как бы неподвижным, а толкатель вращается вокруг оси кулачка с угловой скоростью – ωк.
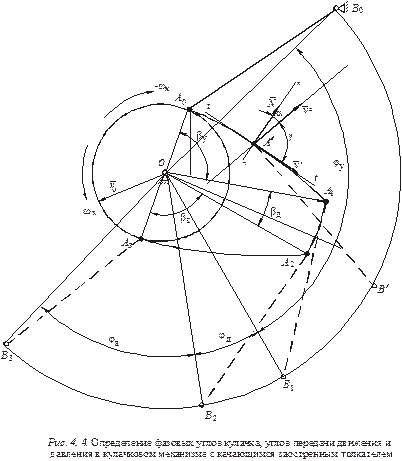
На рис. 4.3 и 4.4 отображены примеры определения с помощью описанного метода фазовых углов кулачка в кулачковых механизмах с соответственно поступательно движущимся и качающимся заостренными толкателями.
На рис. 4.3 контурной линией показано положение толкателя в начале фазы его удаления, когда он контактирует с профилем удаления кулачка в точке А0. При обращении движения толкатель, вращаясь вокруг кулачка с угловой скоростью – ωк, всегда находится на расстоянии е от оси толкателя. Штриховыми линиями отмечены мгновенные положения толкателя при его контакте с профилями удаления и возвращения кулачка в точках А1, А2 и А3. При этом точка А1 соответствует концу фазы удаления толкателя, а точки А2 и А3 – началу и концу фазы его возвращения. Точки пересечения указанных штриховых линий с окружностью минимального радиуса кулачка r0 обозначены цифрами 1 и 2. В соответствии с обозначениями на рис 4.3 получим:
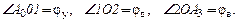
На рис. 4.4, как и на предыдущем, контурной линией показано положение толкателя в начале фазы его удаления, когда он контактирует с кулачком в точке А0. При обращении движения точка В вращается вокруг кулачка с угловой скоростью – ωк, то есть траекторией ее движения является окружность радиусом ОВ0, а точка А скользит по профилю кулачка. Штриховыми линиями отмечены мгновенные положения толкателя при его контакте с профилями удаления и возвращения кулачка в точках А1, А2 и А3. При этом первая точка соответствует концу фазы удаления толкателя, а вторая и третья – началу и концу фазы его возвращения. В соответствии с обозначениями на рис 4.4 получим: 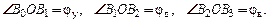
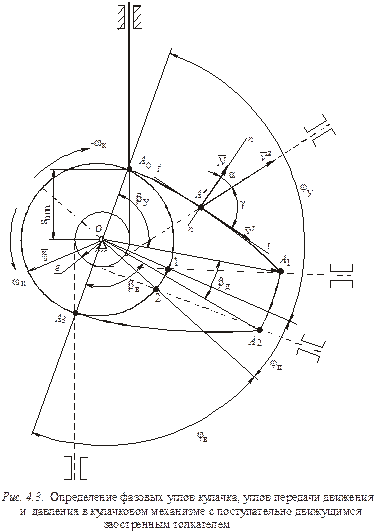
Углы давления и передачи движения кулачкового механизма характеризуют условия силового взаимодействия кулачка с толкателем.
Угол передачи движения γ (рис. 4.3 и 4.4) – острый угол между вектором абсолютной скорости толкателя 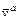 и вектором его относительной скорости
и вектором его относительной скорости 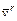 . Вектор
. Вектор 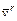 располагается на касательной t-t к профилю кулачка.
располагается на касательной t-t к профилю кулачка.
Угол давления α – острый угол между вектором абсолютной скорости толкателя 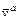 и силой нормального давления
и силой нормального давления 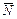 , которая располагается на нормали n-n к профилю кулачка.
, которая располагается на нормали n-n к профилю кулачка.
Углы α и γ, показанные на рис. 4.3 и 4.4 в точках 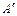 , связаны между собой зависимостью
, связаны между собой зависимостью
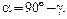
4.2. Описание прибора для построения профиля кулачка
Для построения профиля кулачка используется прибор, который изображен на рис. 4.5. В левой части корпуса 1,прибора смонтированы диск 2 и фрикционное устройство 3 для поворота данного диска. На диске 2 нанесена шкала, градуированная от 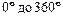 и имеющая двойную оцифровку (через
и имеющая двойную оцифровку (через 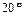 в обоих направлениях) для отсчета углов поворота диска. Отсчетная риска 4 этой шкалы выполнена на кронштейне 5, закрепленном на корпусе 1.
в обоих направлениях) для отсчета углов поворота диска. Отсчетная риска 4 этой шкалы выполнена на кронштейне 5, закрепленном на корпусе 1.

Для обеспечения устойчивого положения бумажного круга, на котором вычерчивается профиль кулачка, на диске 2 расположены четыре иглы (одна из них в его центре), на которые этот круг накалывается и фиксируется прижимом 6.
Установка требуемого углового положения диска 2 производится при помощи фрикционного устройства 3, которое состоит из валика с резиновым кольцом и оси, вмонтированной в корпус 1.
Данный валик с резиновым кольцом прижимается к диску при помощи плоской пружины. Во избежание ее поломки предусмотрен упор.
В правой части смонтирована продольная каретка 7, на которой установлена поперечная каретка 8. Эти каретки могут перемещаться вручную при помощи винтов 9 и 10 соответственно. Отсчет перемещений кареток производится по имеющимся на их направляющих миллиметровым шкалам.
На поперечной каретке 8 закреплен кронштейн 11 с осью 12, на которой свободно установлено коромысло 13 с градуированным сектором 14 и червячным сектором 15, поворот которого осуществляется червяком 16 с отсчетом угла поворота по риске, выполненной на пластине, присоединенной к поперечной каретке 8. В пазу коромысла 13 установлено и закреплено винтом циркульное устройство 17, которое может перемещаться вдоль коромысла. Это устройство включает в себя, помимо указанного винта, корпус с рисками для его установки по миллиметровым шкалам коромысла 13, втулку, цангу, пружину, иглу и гайку для крепления грифеля.
4.3. Порядок выполнения работы
4.3.1. Построение профиля кулачка кулачкового механизма с поступательно движущимся роликовым толкателем
Исходные данные для построения профиля кулачка:
1. Закон изменения аналога ускорения толкателя 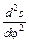
2. Фазовые углы удаления φу, возвращения φв и дальнего стояния φд кулачка.
3. Ход толкателя h.
4. Эксцентриситет е.
5. Наименьшее удаление толкателя smin (минимальное расстояние от оси ролика толкателя до плоскости, проведенной через ось вращения кулачка перпендикулярно линии перемещения толкателя).
Последовательность построения профиля кулачка
1. Выбрать из таблицы 4.1 исходные данные, соответствующие заданному варианту работы, принимая во внимание, что параметр В является постоянной величиной.
2. Интегрируя заданное уравнение изменения аналога ускорения толкателя 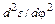 , найти уравнение движения толкателя
, найти уравнение движения толкателя 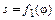 для фазы его удаления.
для фазы его удаления.
3. Выбрать 6…10 значений угла φ поворота кулачка в интервале 0… 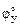 . Из уравнения
. Из уравнения 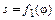 определить значения s перемещения толкателя, соответствующие выбранным значениям угла φ. Полученные данные представить в виде табличной зависимости s от φ.
определить значения s перемещения толкателя, соответствующие выбранным значениям угла φ. Полученные данные представить в виде табличной зависимости s от φ.
4. Аналогично найти уравнение движения толкателя 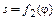 для фазы его возвращения и составить табличную зависимость s от φ.
для фазы его возвращения и составить табличную зависимость s от φ.
5. Установить и закрепить на диске 2 бумажный круг.
6. Настроить прибор в исходное положение. Для этого установить перемещением поперечной каретки 8 (рис. 4.5) заданную величину е, а перемещением продольной каретки 7 и циркульного устройства 17 – заданную величину smin.
Перемещение продольной каретки 7 соответствует перемещению s толкателя. Поэтому при настройке прибора необходимо дать возможность продольной каретке 7 в дальнейшем переместиться на величину h вправо (от центра вращения кулачка). Следовательно, циркульное устройство на коромысле 13 должно стоять на отметке 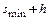 от левого конца этого коромысла.
от левого конца этого коромысла.
7. Для ряда относительных положений кулачка и толкателя, определяемых выбранными значениями φ и расчетными значениями s, провести окружности (каждая из них рассматривается как окружность ролика толкателя) с помощью циркульного устройства. Указанные действия выполнить сначала для фазы удаления толкателя, затем для фазы его дальнего стояния, фазы возвращения и фазы ближнего стояния. При этом следует учесть, что для фаз ближнего и дальнего стояния толкателя значения s не меняются и равны значениям s соответственно в конце и в начале фазы удаления толкателя.
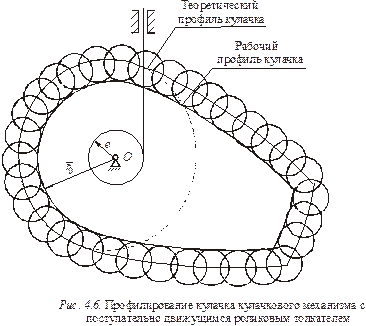
8. Соединить плавной кривой центры этих окружностей. Полученная кривая будет определять теоретический профиль кулачка (рис. 4.6).
Провести огибающую положений данных окружностей, расположенную внутри контура теоретического профиля. Эта огибающая, эквидистантная теоретическому профилю, будет представлять собой рабочий профиль кулачка.
9. На бумажном круге, где вычерчены указанные профили кулачка, нарисовать толкатель и показать параметры h и 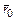 , а также профильные и фазовые углы кулачка βу, βд, βв, φу, φд и φв. За основу при построении углов взять теоретический профиль кулачка.
, а также профильные и фазовые углы кулачка βу, βд, βв, φу, φд и φв. За основу при построении углов взять теоретический профиль кулачка.
10. Определить угол передачи движения γ и угол давления α в двух точках теоретического профиля кулачка, одна из которых расположена на участке этого профиля, обеспечивающем удаление толкателя, а другая – на участке, обеспечивающем возвращение толкателя. Пример определения этих углов показан на рис. 4.3.
4.3.2. Построение профиля кулачка кулачкового механизма с качающимся роликовым толкателем
4.3.2.1. Исходные данные для построения профиля кулачка
1. Закон изменения аналога ускорения толкателя 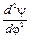 .
.
2. Фазовые углы удаления φу, возвращения φв и дальнего стояния φд кулачка.
3. Длина толкателя L.
4. Расстояние D между осями вращения кулачка и толкателя.
5. Наибольший угол поворота толкателя ψmax.
6. Угол начального положения толкателя ψ0 (угол между толкателем в начале фазы его удаления и прямой, соединяющей оси вращения кулачка и толкателя).
Последовательность построения профиля кулачка
1. Выбрать из таблицы 4.2 исходные данные, соответствующие заданному варианту работы, считая параметр В постоянной величиной.
2. Интегрируя заданное уравнение изменения аналога ускорения толкателя 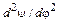 , найти уравнение движения толкателя
, найти уравнение движения толкателя 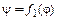 для фазы его удаления.
для фазы его удаления.
3. Выбрать 6…10 значений угла φ поворота кулачка в интервале 0… 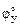 . Из уравнения
. Из уравнения 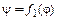 определить значение ψ углов поворота толкателя, соответствующие выбранным значениям угла φ. Полученные данные представить в виде табличной зависимости ψ от φ.
определить значение ψ углов поворота толкателя, соответствующие выбранным значениям угла φ. Полученные данные представить в виде табличной зависимости ψ от φ.
4. Аналогично найти уравнение движения толкателя 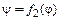 для фазы его возвращения и составить табличную зависимость ψ от φ.
для фазы его возвращения и составить табличную зависимость ψ от φ.
5. Установить и закрепить на диске 2 бумажный круг.
6. Настроить прибор в исходное положение. Для этого установить:
– перемещением циркульного устройства 17 (рис. 4.5) заданную величину L;
– перемещением продольной каретки 7 заданную величину D;
– перемещением коромысла 13 заданную величину ψ0.
7. Для ряда относительных положений кулачка и толкателя, определяемых выбранными значениями φ и расчетными значениями ψ, провести окружности (каждая из них рассматривается как окружность ролика толкателя) с помощью циркульного устройства. Указанные действия выполнить сначала для фазы удаления толкателя, затем для фазы его дальнего стояния, фазы возвращения и фазы ближнего стояния. При этом следует учесть, что для фаз ближнего и дальнего стояния толкателя значения ψ не меняются и равны значениям ψ соответственно в конце и в начале фазы удаления толкателя.
8. Соединить плавной кривой центры этих окружностей. Полученная кривая будет определять теоретический профиль кулачка (рис. 4.7).
Провести огибающую положений данных окружностей, расположенную внутри контура теоретического профиля. Эта огибающая, эквидистантная теоретическому профилю, будет представлять собой рабочий профиль кулачка.
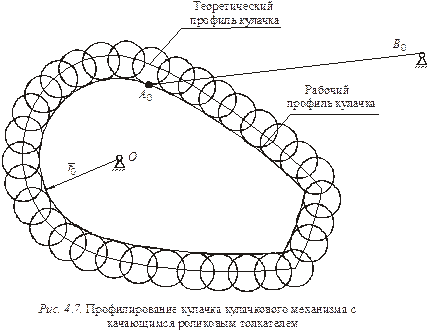
9. На бумажном круге, где вычерчены указанные профили кулачка, нарисовать толкатель и показать углы ψ0 и ψmax, а также профильные и фазовые углы кулачка βу, βд, βв, φу, φд и φв. За основу при построении углов взять теоретический профиль кулачка.
10. Определить угол передачи движения γ и угол давления α в двух точках теоретического профиля кулачка, одна из которых расположена на участке этого профиля, обеспечивающем удаление толкателя, а другая – на участке, обеспечивающем возвращение толкателя. Пример определения этих углов показан на рис. 4.4.
4.4. Примеры определения уравнения движения толкателя
4.4.1. Определение уравнения движения поступательно движущегося толкателя
Исходные данные:
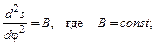 (4.1)
(4.1)
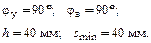
Решение
Интегрируя дважды уравнение (4.1) получим:
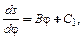 (4.2)
(4.2)
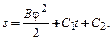 (4.3)
(4.3)
Находим значения коэффициентов интегрирования С1 и С2, а также параметра В для фазы удаления толкателя. Для этого запишем начальные условия:
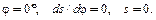 (4.4)
(4.4)
Подставив условия (4.4) в уравнения (4.2) и (4.3), получим
С1 = 0 и С2 = 0 (4.5)
Запишем конечные условия:
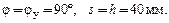 (4.6)
(4.6)
Подставив коэффициенты (4.5) и условия (4.6) в выражение (4.3), получим
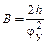 . (4.7)
. (4.7)
С учетом (4.7) и (4.5) уравнение движения толкателя для фазы его удаления примет вид:
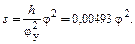 (4.8)
(4.8)
Выбрав десять значений угла φ в интервале 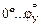 и используя уравнение (4.8), строим табличную зависимость s от φ:
и используя уравнение (4.8), строим табличную зависимость s от φ:
| φ, град | ||||||||||
| s, мм | 0,0 | 0,5 | 2,0 | 4,4 | 7,9 | 12,3 | 17,8 | 24,2 | 31,6 | 40,0 |
Находим значения коэффициентов С1 и С2, а также параметра В для фазы возвращения толкателя. Для этого запишем начальные условия:
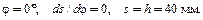 (4.9)
(4.9)
Подставив условия (4.9) в уравнения (4.2) и (4.3), получим
С1 = 0 и С2 = h = 40 мм. (4.10)
Запишем конечные условия:
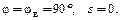 (4.11)
(4.11)
Подставив коэффициенты (4.10) и условия (4.11) в выражение (4.3), получим
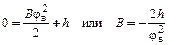 . (4.12)
. (4.12)
С учетом (4.12) и (4.10) уравнение движения толкателя для фазы его возвращения примет вид:
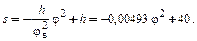 (4.13)
(4.13)
Выбрав десять значений угла φ в интервале 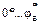 и используя уравнение (4.13), строим табличную зависимость s от φ:
и используя уравнение (4.13), строим табличную зависимость s от φ:
| φ, град | ||||||||||
| s, мм | 39,5 | 38,0 | 35,6 | 32,1 | 27,1 | 22,2 | 15,8 | 8,4 | 0,0 |
4.4.2.Определение уравнения движения качающегося толкателя
Исходные данные

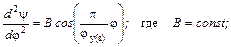 (4.14)
(4.14)
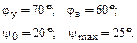
Решение
Интегрируя уравнение (4.14) дважды получим:
