ПРОСТЫЕ ВИДЫ СОПРОТИВЛЕНИЯ. ПЛОСКИЙ ИЗГИБ
1.4. Определение внутренних усилий. Метод мысленных сечений
Итак, в сопротивлении материалов не учитывается реальная атомная структура материала твердого тела. Исходя из этого, сплошность и однородность тела обеспечивается не межатомными силами, а гипотетическими внутренними усилиями.
Внутренние усилия – силы взаимодействия (сцепления) между частицами тела, возникающие внутри элемента конструкции, как противодействие внешнему нагружению.
Внутренние усилия во всех случаях стремятся сохранить тело как единое целое, противодействуя всякой попытке изменить взаимное расположение частиц, т. е. деформировать и разрушить тело. Поэтому именно величиной внутренних усилий определяется возможность разрушения в том или ином опасном сечении элемента конструкции. Таким образом, для решения задач сопротивления материалов необходимо уметь выявлять, а затем определять величину и направление внутренних усилий. При их нахождении широко используется метод мысленных сечений.
Выполнение гипотезы сплошности твердого деформируемого тела обеспечивается внутренними связями, природа которых не рассматривается в сопротивлении материалов. Разрезая тело какой-либо плоскостью, мы мысленно разрушаем эти связи, но для равновесия системы заменяем нарушенные связи силами, которые называются внутренними. Для их определения следует рассмотреть равновесие любой части тела по одну сторону от плоскости мысленного сечения.
Необходимо подчеркнуть, что из уравнений равновесия для оставленной части тела определяется не закон распределения внутренних сил, а их статический эквивалент в выбранной точке приведения, то есть главный вектор с проекциями N, Qy, Qz и главный момент с проекциями Mx, My, Mz. В сопротивлении материалов эти проекции часто называют внутренними усилиями.
Метод мысленных сечений позволяет отбросить ненужный для расчета элемент конструкции (или часть этого элемента), заменить его силой, действие которой будет эквивалентно действию отброшенного элемента (его части).
Если задача статически определима, то для определения этой силы достаточно использовать уравнения равновесия (уравнения статики).
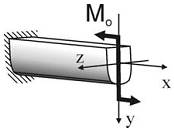
Рассмотрим какой-либо элемент (например, брус), находящийся в равновесии под действием внешних сил. Пусть требуется определить внутренние усилия в произвольном сечении бруса.
Применим для этого метод мысленных сечений:
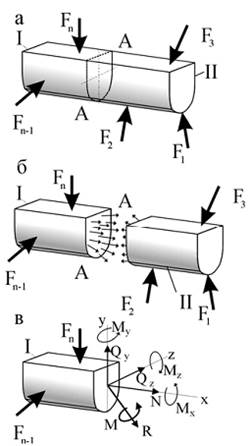а) мысленно рассечем элемент плоскостью А – А;
б) отбросим ненужную (наиболее сложно нагруженную) часть элемента, действие отброшенной части заменим внутренними усилиями;
в) внутренние усилия приведем к главному вектору R и главному моменту M, главный вектор и главный момент разложим по трем взаимно перпендикулярным осям x, y и z (ось x – нормальна к сечению элемента);
г) внутренние усилия (N, Qy, Qz, Mx, My, Mz) определим из уравнений равновесия оставшейся части элемента
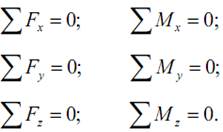
N – осевое (продольное) усилие. Осевое усилие равно сумме проекций на ось x всех внешних сил, действующих с одной стороны сечения:
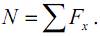
Осевое усилие вызывает растяжение (сжатие) элемента.
Qy, Qz – поперечные силы. Поперечные силы равны сумме проекций всех внешних сил (с одной стороны сечения) на оси y и z соответственно:
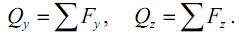
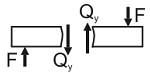
Поперечные силы вызывают сдвиг в сечении элемента.
Mx – крутящий момент (T, Mкр). Крутящий момент равен сумме моментов внешних сил (с одной стороны сечения) относительно оси x:
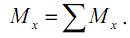
Крутящий момент вызывает кручение элемента.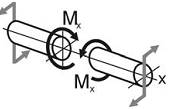 
My, Mz – изгибающие моменты. Изгибающие моменты равны сумме моментов внешних сил относительно осей y и z соответственно:
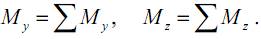
Изгибающие моменты вызывают изгиб элемента.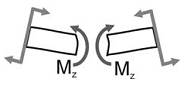 
Таким образом, введя понятие внутренних усилий, мы получили возможность свести все многообразие внешних нагрузок и конфигураций элементов к 6-ти силовым факторам (N, Qy, Qz, Mx, My, Mz) и представить даже самое сложное внешнее воздействие как сочетание 4-х видов нагружения: растяжения, сдвига, кручения, изгиба.
Следовательно, если полная система внешних сил известна, то по методу сечений, всегда можно определить все внутренние усилия действующих в произвольно взятом сечении тела. Данное положение является основополагающим обстоятельством в механике твердого деформируемого тела.
Сопротивления, при которых в поперечном сечении бруса действует одно внутреннее усилие, условно называются простыми. При одновременном действии в сечении бруса двух и более усилий сопротивление бруса называется сложным.
При выполнении практических расчетов, для наглядности, как правило, определяются графики функций внутренних силовых факторов относительно координатной оси, направленной вдоль продольной оси стержня. Графики изменения внутренних усилий вдоль продольной оси стержня называются эпюрами.
1.5. Понятие о нормальных и касательных напряжениях
Установить закон (характер) распределения внутренних усилий по сечению элемента методами статики не представляется возможным: составляя уравнения равновесия для сил, приложенных к отсеченной части элемента, можем найти лишь статический эквивалент внутренних усилий, возникающих в рассматриваемом сечении. Чтобы характеризовать закон распределения внутренних усилий по сечению элемента, необходимо ввести для них числовую меру. За такую меру принимается напряжение.
В сопротивлении материалов неявно предполагается, что внутренние усилия достаточно равномерно распределены на малой площадке в окрестности любой точки мысленного сечения. Поэтому отношение главного момента к величине площадки стремится к нулю вместе с этой площадкой. В результате
на данной площадке dA остается главный вектор сил dR, отношение которого
к величине площадки dA при стягивании последней в точку, называется полным напряжением p:
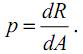
Напряжение– есть внутренняя сила, отнесенная к единице площади в данной точке рассматриваемого сечения (иначе говоря, интенсивность внутреннего усилия в данной точке сечения).
Размерность напряжения: Н/м2, то есть Па (МПа, кПа)
В расчетах удобнее пользоваться не полным напряжением p, а его нормальной σ и касательными τ составляющими. Рассмотрим эти понятия.
Проекциями вектора dR на оси x, y, z будут элементарное осевое усилие dN и элементарные поперечные силы dQy, dQz. Разделив величины dN, dQy, dQz на бесконечно малую площадь dA, получим величины продольных и поперечных сил, приходящихся на единицу площади в данной точке сечения.
Нормальное напряжение (σx) – интенсивность осевого внутреннего усилия, или осевое усилие, приходящееся на единицу площади в данной точке рассматриваемого сечения
Касательное напряжение (τy, τz)– интенсивность внутренних поперечных сил, или поперечная сила, приходящаяся на единицу площади в данной точке рассматриваемого сечения
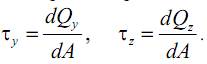
Таким образом, на площадке могут возникать два вида напряжений: нормальные и касательные. В соответствии с двумя видами напряжений на наиболее опасной площадке (там, где напряжения максимальны) может реализовываться два различных механизма разрушения – отрыв или срез.
ПРОСТЫЕ ВИДЫ СОПРОТИВЛЕНИЯ. ПЛОСКИЙ ИЗГИБ
10.1. Общие понятия и определения
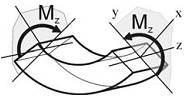Изгиб – это такой вид нагружения, при котором стержень загружен моментами в плоскостях, проходящих через продольную ось стержня.
Стержень, работающий на изгиб, называется балкой (или брусом ). В дальнейшем будем рассматривать прямолинейные балки, поперечное сечение которых имеет хотя бы одну ось симметрии.
В сопротивлении материалов различают изгиб плоский, косой и сложный.
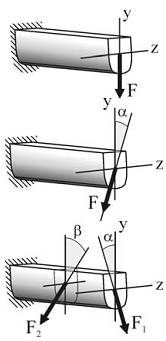
Плоский изгиб – изгиб, при котором все усилия, изгибающие балку, лежат в одной из плоскостей симметрии балки (в одной из главных плоскостей).
Главными плоскоcтями инерции балки называют плоскости, проходящие через главные оси поперечных сечений и геометрическую ось балки (ось x).
Косой изгиб – изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.
Сложный изгиб – изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях.
Далее будем рассматривать плоский изгиб, то есть все силы будем прилагать в плоскости симметрии балки.
10.2. Определение внутренних усилий при изгибе
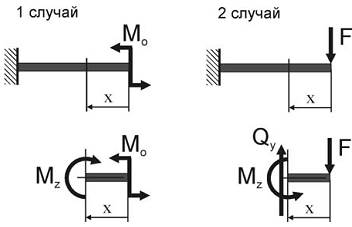Рассмотрим два характерных случая изгиба: в первом – консольная балка изгибается сосредоточенным моментом Mo; во втором – сосредоточенной силой F.
Используя метод мысленных сечений и составляя уравнения равновесия для отсеченных частей балки, определим внутренние усилия в том и другом случае:
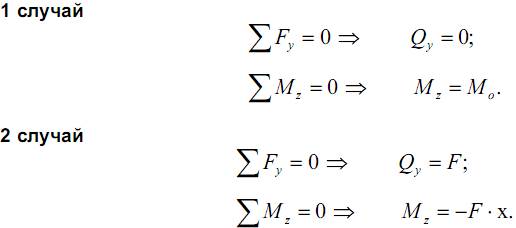
Остальные уравнения равновесия, очевидно, тождественно равны нулю.
Таким образом, в общем случае плоского изгиба в сечении балки из шести внутренних усилий возникает два – изгибающий момент Мz и поперечная сила Qy (или при изгибе относительно другой главной оси – изгибающий момент Мy и поперечная сила Qz).
При этом, в соответствии с двумя рассмотренными случаями нагружения, плоский изгиб можно подразделить на чистый и поперечный .
Чистый изгиб – плоский изгиб, при котором в сечениях стержня из шести внутренних усилий возникает только одно – изгибающий момент (см. первый случай).
Поперечный изгиб – изгиб, при котором в сечениях стержня кроме внутреннего изгибающего момента возникает и поперечная сила (см. второй случай).
Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.
При определении внутренних усилий будем придерживаться следующего правила знаков:
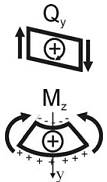1) поперечная сила Qy считается положительной, если она стремится повернуть рассматриваемый элемент балки по часовой стрелке;
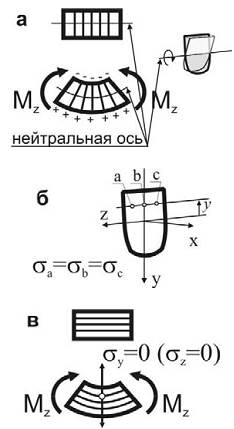
2) изгибающий момент Мz считается положительным, если при изгибе элемента балки верхние волокна элемента оказываются сжатыми, а нижние – растянутыми (правило зонта).
Таким образом, решение задачи по определению внутренних усилий при изгибе будем выстраивать по следующему плану: 1) на первом этапе, рассматривая условия равновесия конструкции в целом, определяем, если это необходимо, неизвестные реакции опор (отметим, что для консольной балки реакции в заделке можно и не находить, если рассматривать балку со свободного конца); 2) на втором этапе выделяем характерные участки балки, принимая за границы участков точки приложения сил, точки изменения формы или размеров балки, точки закрепления балки; 3) на третьем этапе определяем внутренние усилия в сечениях балки, рассматривая условия равновесия элементов балки на каждом из участков.
10.3. Дифференциальные зависимости при изгибе
Установим некоторые взаимосвязи между внутренними усилиями и внешними нагрузками при изгибе, а также характерные особенности эпюр Q и M, знание которых облегчит построение эпюр и позволит контролировать их правильность. Для удобства записи будем обозначать: M≡Mz, Q≡Qy.
Выделим на участке балки с произвольной нагрузкой в месте, где нет сосредоточенных сил и моментов, малый элемент dx. Так как вся балка находится в равновесии, то и элемент dx будет находиться в равновесии под действием приложенных к нему поперечных сил, изгибающих моментов и внешней нагрузки. Поскольку Q и M в общем случае меняются вдоль
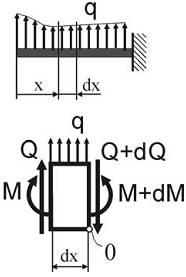оси балки, то в сечениях элемента dx будут возникать поперечные силы Q и Q+dQ, а также изгибающие моменты M и M+dM. Из условия равновесия выделенного элемента получим
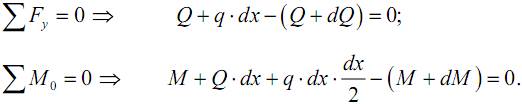
Первое из двух записанных уравнений дает условие
Из второго уравнения, пренебрегая слагаемым q·dx·(dx/2) как бесконечно малой величиной второго порядка, найдем
Рассматривая выражения (10.1) и (10.2) совместно можем получить
Соотношения (10.1), (10.2) и (10.3) называют дифференциальными зависимостями Д. И. Журавского при изгибе.
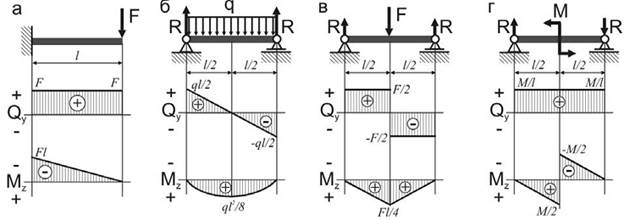
Анализ приведенных выше дифференциальных зависимостей при изгибе позволяет установить некоторые особенности (правила) построения эпюр изгибающих моментов и поперечных сил: а – на участках, где нет распределенной нагрузки q, эпюры Q ограничены прямыми, параллельными базе, а эпюры M – наклонными прямыми; б – на участках, где к балке приложена распределенная нагрузка q, эпюры Q ограничены наклонными прямыми, а эпюры M – квадратичными параболами.
При этом, если эпюру М строим «на растянутом волокне», то выпуклость параболы будет направлена по направлению действия q, а экстремум будет расположен в сечении, где эпюра Q пересекает базовую линию; в – в сечениях, где к балке прикладывается сосредоточенная сила на эпюре Q будут скачки на величину и в направлении данной силы, а на эпюре М – перегибы, острием направленные в направлении действия этой силы; г – в сечениях, где к балке прикладывается сосредоточенный момент на эпюре Q изменений не будет, а на эпюре М – скачки на величину этого момента; д – на участках, где Q>0, момент М возрастает, а на участках, где Q<0, момент М убывает (см. рисунки а–г).
10.4. Нормальные напряжения при чистом изгибе прямого бруса
Рассмотрим случай чистого плоского изгиба балки и выведем формулу для определения нормальных напряжений для данного случая.
Отметим, что в теории упругости можно получить точную зависи-мость для нормальных напряжений при чистом изгибе, если же решать эту задачу методами сопротивления материалов необходимо ввести некоторые допущения.
Таких гипотез при изгибе три:
а – гипотеза плоских сечений (гипотеза Бернулли) – сечения плоские до деформации остаются плоскими и после деформации, а лишь поворачиваются относительно некоторой линии, которая называется нейтральной осью сечения балки. При этом волокна балки, лежащие с одной стороны от нейтральной оси будут растягиваться, а с другой – сжиматься; волокна, лежащие на нейтральной оси своей длины не изменяют;
б – гипотеза о постоянстве нормальных напряжений – напряжения, действующие на одинаковом расстоянии y от нейтральной оси, постоянны по ширине бруса;
в – гипотеза об отсутствии боковых давлений – соседние продольные волокна не давят друг на друга.
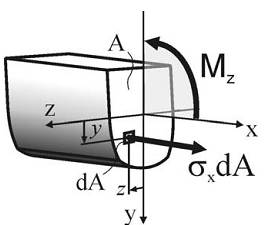Статическая сторона задачи
Чтобы определить напряжения в поперечных сечениях балки, рассмотрим, прежде всего, статическую сторон у задачи . Применяя метод мысленных сечений и составляя уравнения равновесия для отсеченной части балки, найдем внутренние усилия при изгибе. Как было показано ранее, единственным внутренним усилием, действующим в сечении бруса при чистом изгибе, является внутренний изгибающий момент, а значит здесь возникнут связанные с ним нормальные напряжения.
Связь между внутренними усилиями и нормальными напряжениями в сечении балки найдем из рассмотрения напряжений на элементарной площадке dA, выделенной в поперечном сечении A балки в точке с координатами y и z (ось y для удобства анализа направлена вниз):
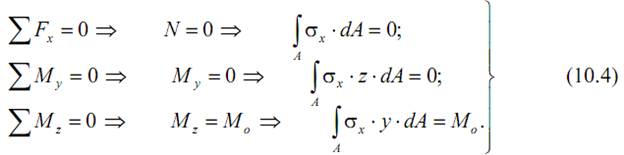
Как видим, задача является внутренне статически неопределимой, так как неизвестен характер распределения нормальных напряжений по сечению. Для решения задачи рассмотрим геометрическую картину деформаций.
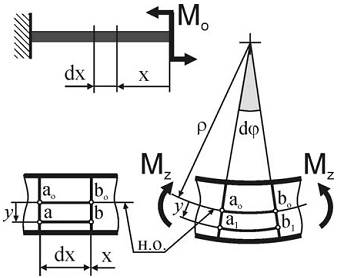Геометрическая сторона задачи
Рассмотрим деформацию элемента балки длиной dx, выделенного из изгибаемого стержня в произвольной точке с координатой x. Учитывая принятую ранее гипотезу плоских сечений, после изгиба сечения балки повернуться относительно нейтральной оси (н.о.) на угол dϕ, при этом волокно ab, отстоящее от нейтральной оси на расстояние y, превратится в дугу окружности a1b1, а его длина изменится на некоторую величину. Здесь напомним, что длина волокон, лежащих на нейтральной оси, не изменяется, а потому дуга a0b0 (радиус кривизны которой обозначим ρ) имеет ту же длину, что и отрезок a0b0 до деформации a0b0=dx.
Найдем относительную линейную деформацию εx волокна ab изогнутой балки:
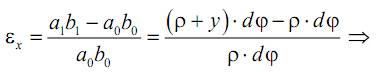
Дата добавления: 2015-02-07; просмотров: 2683;