Использование делегата для передачи метода в качестве параметра в другой метод
До сих пор в качестве параметров методов использовались простые переменные или массивы. Но параметром метода может быть также и другой метод. В качестве наглядного примера рассмотрим следующую задачу. Пусть требуется вычислить две суммы
S1 = 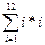
S2 = 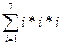
Вычисление суммы в методе оформим в общем виде, не конкретизируя зависимость члена суммы от его номера, т.е. оформим функцию для вычисления суммы
S = 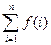 .
.
Функция f должна быть включена в список формальных параметров как переменная типа делегат, которая при каждом обращении должна быть заменена фактическим параметром, т.е. именем метода, описывающего вычисление конкретного члена суммы.
Делегат могут вызывать только такие методы, у которых тип возвращаемого значения и список параметров совпадают с соответствующими элементами объявления делегата.
Ключевое слово delegate используется для объявления ссылочного типа. Делегат это тип, который определяет подпись метода и его можно связать с любым методом с совместимой подписью.
Пример 5.5. В качестве примера приводится программа для решения рассмотренной выше задачи вычисления двух сумм.
using System;
class Program
{
delegate int fi(int i);
static int f1(int i)
{
return i * i;
}
static int f2(int i)
{
return i * i * i;
}
static int si(fi f, int n)
{
int s = 0;
for (int i = 0; i <= n; i++)
{
s = s + f(i);
}
return s;
}
static void Main()
{
int s1 = si(f1,12);
int s2 = si(f2,7);
Console.WriteLine("{0} {1}", s1, s2);
}
}

Следующие примеры демонстрируют использование метода в качестве параметра, а также использование перечисления для вычисления определенного интеграла двумя различными методами.
Пример 5.6. Оформить функцию для вычисления S = 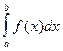 . Используя эту функцию, вычислить S1=
. Используя эту функцию, вычислить S1= 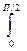 sin
sin  xdx и S2=
xdx и S2= 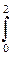 1/
1/ 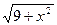 dx.
dx.  Для вычисления определенного интеграла использовать метод трапеций. Разделим отрезок [a,b] на n отрезков длиной h=(b–a)/n. Формула трапеций для вычисления интеграла в этом случае имеет вид
Для вычисления определенного интеграла использовать метод трапеций. Разделим отрезок [a,b] на n отрезков длиной h=(b–a)/n. Формула трапеций для вычисления интеграла в этом случае имеет вид
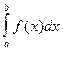
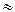 h/2(f(a)+f(b)+2
h/2(f(a)+f(b)+2 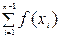 ),
),
где x1 = a+h, x2 = a+2h, ..., …
Выберем n =20 для вычисления S1 и n =30 для вычисления S2.
using System;
class Program
{
delegate double fx(double i);
static double f1(double x)
{
return Math.Sin(x)*Math.Sin(x);
}
static double f2(double x)
{
return 1/Math.Sqrt(9 + x * x);
}
static double sw(fx f, double a, double b, int n)
{
double c = 0, x = a, h = (b - a)/n;
for (int i = 1; i < n; i++)
{
x += h; c += f(x);
}
return (2 * c + f(a) + f(b)) * h / 2;
}
static void Main()
{
double s1 = sw(f1, 0.0, Math.PI/2, 20);
double s2 = sw(f2, 0.0, 2.0, 30);
Console.WriteLine("{0:f4} {1:f4}", s1, s2);
}
}

Пример 5.7. Оформить функцию для вычисления S = 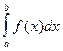 . Используя эту функцию, вычислить S1=
. Используя эту функцию, вычислить S1= 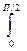 sin
sin  xdx и S2=
xdx и S2= 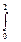 1/
1/ 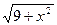 dx.
dx.  Для вычисления определенного интеграла использовать метод трапеций и метод Симпсона. Для выбора метода использовать перечисление (см. п. 1.6).
Для вычисления определенного интеграла использовать метод трапеций и метод Симпсона. Для выбора метода использовать перечисление (см. п. 1.6).
Разделим отрезок [a,b] на n отрезков (для метода Симпсона n должно быть четным) длиной h=(b–a)/n. Формула трапеций для вычисления интеграла приведена выше.
Формула Симпсона имеет вид
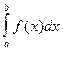
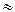 h/3(f(a)+f(b)+
h/3(f(a)+f(b)+ 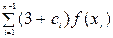
(ci=(-1)i+1, вычисляется как c = -c).
Выберем n =20 для вычисления S1 и n =30 для вычисления S2.
using System;
class Program
{
enum Method { method1, method2 };//объявление перечисления
delegate double fx(double i);
static double f1(double x)
{
return Math.Sin(x) * Math.Sin(x);
}
static double f2(double x)
{
return 1 / Math.Sqrt(9 + x * x);
}
static double sw(fx f, double a, double b, int n, Method met)
{
double s = f(a) + f(b), x = a, h = (b - a) / n;
if (met == Method.method1)
{
for (int i = 1; i < n; i++)
{
x += h; s += 2 * f(x);
}
s = s * h / 2;
}
if (met == Method.method2)
{
double c = 1.0;
for (int i = 1; i < n; i++)
{
x += h; s += (3 + c) * f(x); c = -c;
}
s = s * h / 3;
}
return s;
}
static void Main()
{
double s1 = sw(f1, 0.0, Math.PI / 2, 20, Method.method1);
double s11 = sw(f1, 0.0, Math.PI / 2, 20, Method.method2);
double s2 = sw(f2, 0.0, 2.0, 30, Method.method1);
double s22 = sw(f2, 0.0, 2.0, 30, Method.method2);
Console.WriteLine("{0:f4} {1:f4} {2:f4} {3:f4}", s1, s11, s2, s22);
Console.ReadKey();
}
}
Замечание.Среди параметров метода sw для вычисления интеграла имеется параметр met типа Method. При вызове метода в качестве аргумента указывается конкретный элемент списка перечисления, объявленного в начале кода, в соответствии с чем и выбирается способ вычисления интеграла в методе sw.

Вопросы для самопроверки.
1. Что такое метод. Разновидности методов: метод, возвращающий значение и метод, не возвращающий значения. Особенности их оформления.
2. Что такое подпись метода.
3. Вызов метода. Способы передачи параметров: по значению, по ссылке. Правила согласования типов параметров метода и аргументов при обращении к нему.
4. Различные возможности взаимного расположения вызываемого и вызывающего методов: в одном классе, в разных классах.
5. Особенности вызова нестатического метода из статического метода.
6. Использование массивов в качестве параметров.
7. Методы как параметры: Использование делегата для передачи метода как параметра другого метода.
Дата добавления: 2015-02-07; просмотров: 1495;
