Задание для самостоятельного выполнения.

1. Определить, сколькими способами можно отобрать команду в составе пяти человек из восьми кандидатов; из 10 кандидатов; из 11 кандидатов. Использовать метод для подсчёта количества способов отбора по формуле .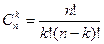

2. Два треугольника заданы длинами своих сторон a, b и с. Определить треугольник с большей площадью, вычисляя площади треугольников по формуле Герона 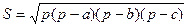, где p = (a + b + c)/2.

3. .Два велосипедиста одновременно начинают движение из одной точки. Первый начинает движение со скоростью 10 км/ч и равномерно увеличивает скорость на 1 км/ч. Второй начинает движение со скоростью 9 км/ч и равномерно увеличивает скорость на 1.6 км/ч. Определить:

a. какой спортсмен преодолеет большее расстояние через 1 ч; через 4 ч;

b. когда второй спортсмен догонит первого.

Использовать метод для вычисление пути в зависимости от времени по формуле S = vt + at²/2, где v - начальная скорость, а - ускорение.

4. Поменять местами максимальные элементы матриц А размером 5*6 и В размером 3*5. Поиск максимального элемента матрицы осуществить в методе.

5. В массивах А размером 9 и В размером 7 заменить максимальные элементы на среднее арифметическое значение элементов, расположенных после максимального, в том массиве, для которого максимальный элемент расположен дальше от конца массива. Поиск максимального элемента осуществить в методе.

6. В матрицах В размером 5*5 и С размером 6*6 удалить строку, содержащую максимальный элемент на диагонали. Поиск максимального элемента диагонали осуществить в методе.

7. Поменять местами строку матрицы А размером 5*5 и столбец матрицы В размером 5*5, содержащие максимальные элементы на диагоналях. Поиск максимального элемента на диагонали осуществить в методе.

8. Поменять местами строки матриц А размером 4*6 и В размером 6*6, содержащие максимальные элементы в 1-м столбце. Поиск максимального элемента в заданном столбце матрицы осуществить в методе.

9. Объединить массивы А размером 7 и В размером 8, предварительно удалив максимальные элементы этих массивов. Результат получить в массиве А. Удаление элемента массива с заданным индексом осуществить в методе.

10. В массив В размером 4*5 вставить после строки, содержащей максимальное количество положительных элементов, столбец массива С размером 5*6, содержащий максимальное количество положительных элементов. Определение количества положительных элементов в заданной строке (или столбце) матрицы осуществить в методе.

11. Упорядочить по возрастанию элементы массивов А размером 9 и В размером 11, расположенные после максимального элемента. Упорядочение части массива, начинающейся элементом с заданным индексом, осуществить в методе.

12. Даны матрицы А размером 6*5 и С размером 7*4. Объединить массивы, сформированные из сумм положительных элементов столбцов матриц А и С. Суммирование положительных элементов столбцов с получением результата в виде массива осуществить в методе.

13. Вычислить суммы 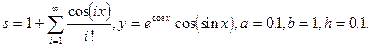и .

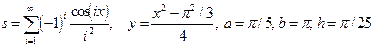Вычисление суммы осуществлять в методе. Для вычисления члена суммы использовать делегата.

14. Японская радиокомпания провела опрос 250 радиослушателей по трем вопросам:

1. 1). Какое животное Вы связываете с Японией и японцами?
2. 2). Какая черта характера присуща японцам больше всего?
3. 3). Какай неодушевленный предмет или понятие Вы связываете с Японией?

Большинство опрошенных прислали ответы на все или часть вопросов. Составить программу получения первых пяти наиболее часто встречающихся ответов по каждому вопросу и доли (в %) каждого такого ответа. Предусмотреть необходимость сжатия столбца ответов в случае отсутствия ответов на некоторые вопросы. Обработку информации по каждому вопросу осуществлять в методе.

15. В двух заданных матрицах одинакового размера поменять строки, содержащие максимальное количество отрицательных элементов. Нахождение количества отрицательных элементов заданной строки матрицы осуществлять в методе. Определение номера строки, содержащей максимальное количество отрицательных элементов, осуществлять в методе.

Указание. К методу, возвращающему значение количества отрицательных элементов заданной строки матрицы, следует обращаться для каждой матрицы столько раз, сколько строк в матрице (в цикле по строкам). В результате должены быть сформированы одномерные массивы, содержащие количества отрицательных элементов в строках матриц. Обращение ко второму методу для каждого одномерного массива позволит определить индексы максимальных элементов этих массивов, т.е. номера строк матриц, которые и следует далее поменять местами.