ФОРМЫ ПРЕДСТАВЛЕНИЯ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ

В разд. 2.5 уже отмечалось, что форма представления из­мерительной информации о физической величине постоянно­го размера зависит от характера ее дальнейшего использова­ния. Если результат измерения является окончательным, то форма представления измерительной информации должна быть удобной для восприятия человеком, например,

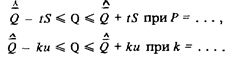
Если результат измерения предназначен для точных вычис­лений, то он должен быть представлен эмпирическим зако­ном распределения вероятности. Если же результат измере­ния предполагается использовать для приближенных вы­числений, то он выражается через числовые характеристи­ки математической модели закона распределения вероятнос­ти, или их точечные оценки: 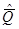; и или Q; S. Такая форма представления измерительной информации называется циф­ровой.

При измерении физической величины, зависящей от вре­мени (или от пространственной координаты после прост­ранственно-временного преобразования), полезный сигнал на выходе средства измерения будет непрерывной (см. рис. 162, а) или дискретной (рис. 162, б) функцией времени. Форма представления измерительной информации, показан­ная на рис. 162, а, называется аналоговой, а на рис. 162, б— дискретной. Так как измерительная информация не должна зависеть от формы ее представления, возникает задача выяс­нения условий, при которых переход от одной формы пред­ставления информации к другой не сопровождается ее поте­рями.

Эта задача в 1933 г. решена В.А. Котельниковым для сиг­налов с ограниченным спектром.

Подобно тому, как сигнал длительностью Т может быть представлен на этом интервале времени рядом Фурье

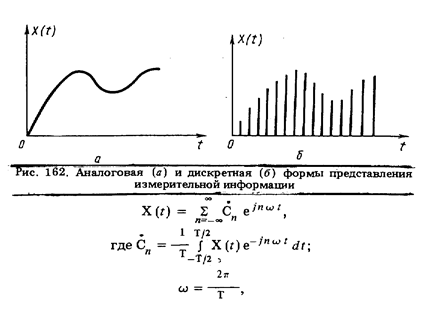
комплексный спектр сигнала с верхней частотой w_в в занима­емой им полосе частот от — w_в до + w_в может быть представ­лен рядом

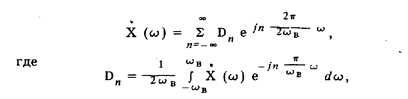
а 2w_в играет роль интервала Т. Для сигнала с ограниченным спектром обратное преобразование Фурье

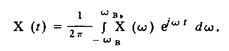
Сравнивая это выражение с формулой для Dn, можно заме­тить что, коэффициенты Dn, представляют собой умноженные на 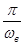значения сигнала Х (t) в моменты времени

t = -n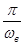

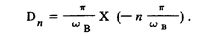
Указанные моменты разделены равными промежутками вре­мени

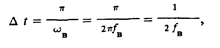
как это показано на рис. 163.

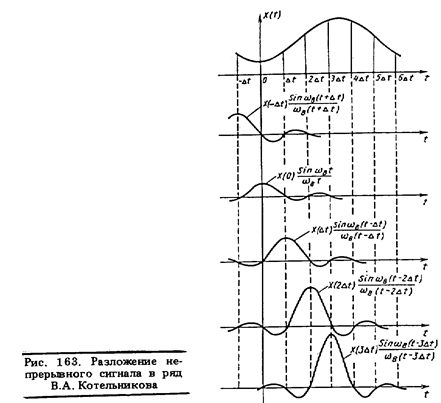
Подставляя в выражение для Х(t) значения Х (w) и D_n,получим

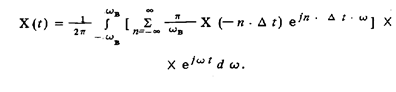
Изменим порядок суммирования и интегрирования:

Результат суммирования не изменится, если у всех п, прини­мающих значения от — ¥ до + ¥, изменить знак на противо­положный. Тогда окончательно

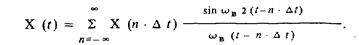
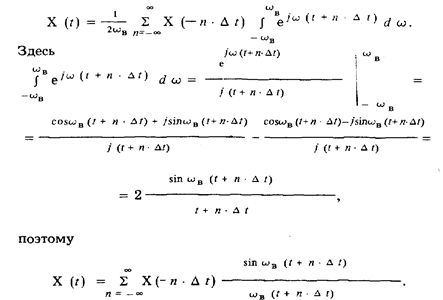
Полученный результат является аналитическим выраже­нием теоремы В.А. Котельникова. Теорема гласит, чтонепре­рывный сигнал с ограниченным спектром может быть пред­ставлен с помощью его мгновенных значений, взятых через промежутки времени

.

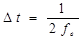Такое представление явля­ется точным. Однако ограниченный спектр имеют сигналы не­ограниченной длительности. На практике же у всех сигналов есть начало и конец, т.е. они являются ограниченными во вре­мени и имеют неограниченный спектр. Для них теорема В.А. Котельникова выполняется приближенно. Так как энер­гия реальных сигналов в основном сосредоточена все-таки в конечной полосе частот, за f_в принимается верхняя частота энергосодержащей части спектра. Общее число дискретных значений получается тогда равным

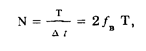
где Т — длительность сигнала.

На рис.163 дана графическая интерпретация разложения непрерывного сигнала в ряд В.А. Котельникова. Члены ряда являются ортогональными функциями на бесконечно боль­шом интервале времени. Они равны мгновенному значению сигнала в один из фиксированных моментов времени n D t, а во все остальные моменты k ·Dt равны нулю. Таким обра­зом, в каждый из моментов времени п · Dt ряд вырождает­ся в одно слагаемое. В промежутках между этими момента­ми члены ряда суммируются.

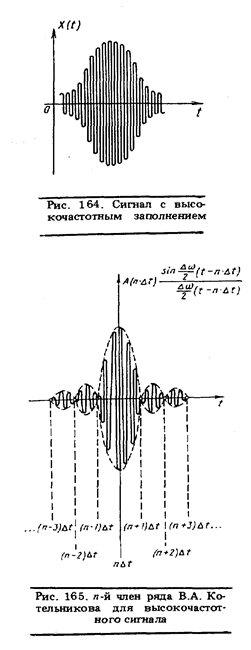
Если сигнал имеет высокочастотное заполнение (см., например, рис. 164), то спектр его не содержит низкочас­тотных составляющих. С хорошим приближением его можно считать ограниченным в полосе частот от f _н до f _в. Теорема В.А. Котельникова в этом случае утверждает, что такой сиг­нал может быть представлен с помощью мгновенных зна­чений его амплитуды и фазы, взятых через промежутки времени

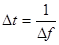, где Df = f_в – f_н

При длительности сигнала, равной Т, количество дискретных значений амплитуды и фа­зы

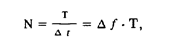
а общее их количество, соответственно, в два раза больше. Доказательство теоремы
В.А. Котельникова в рассмат­риваемом случае аналогично приведенному выше. Ряд
В.А. Котельникова для высокочастотного сигнала имеет вид:

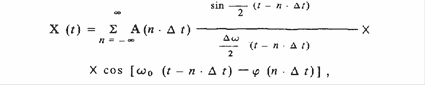
где А (п · Dt) — значение амплитуды (огибающей) высоко частотного сигнала в фиксированный момент времени;

j(n Dt)— значение фазы высокочастотного сигнала в тот же момент времени;

w₀=2p 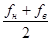— середина полосы час­тот, занимаемой спектром сигнала.

Отдельный член ряда представлен графически на рис. 165. Применение теоремы В.А.Котельникова позволяет без по­тери измерительной информации перейти к цифровой форме ее представления в определенные моменты времени. Переход от текущего времени к дискретному называется квантовани­ем по времени. Наряду с квантованием по времени в техни­ческих системах применяется квантование по уровню, тесно связанное с кодированием.