КОДИРОВАНИЕ
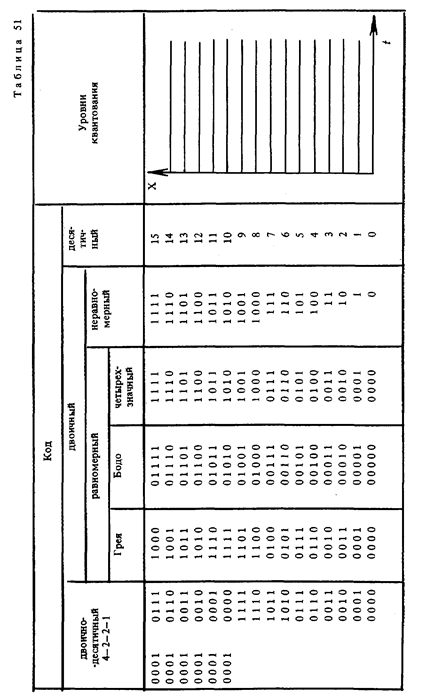
В табл. 51 показаны уровни, которые может превысить сигнал на выходе средства измерений. При этом не существенно, является ли он постоянным, меняющимся во времени или его значение выбрано в фиксированный момент времени п · Δ t. Измерительная информация заключается в том, какой уровень превышен сигналом. Таким образом, информация о значении сигнала оказывается дискретной. Переход к ней называется квантованием, а сами уровни — уровнями квантования сигнала. При равных промежутках между уровнями квантование называется равномерным, при неравных — неравномерным. Наибольшее распространение в технике получило равномерное квантование по уровню.
|
Если будет зафиксировано, что сигнал превысил i-и уровень (но не достиг i + 1-го), то его значение
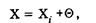
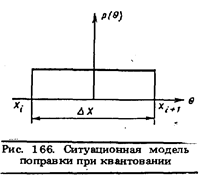
где значение поправки Q может быть любым в пределах от 0 до ΔХ = Х+1 — X,. Ситуационная модель поправки показана на рис. 166. Величина ΔХ называется шагом квантования. Дефицит информации о значении поправки приводит к потере точности. С учетом поправки
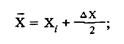
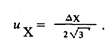
При заданных их и диапазоне изменения сигнала от 0 до Хmax число уровней или ступеней квантования определяется по формуле
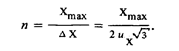
Уровни квантования могут быть обозначены какими-либо символами или пронумерованы, как показано в табл. 51, в десятичной или любой другой системе счисления. Такая операция называется кодированием. Символы или цифры представляют собой кодовые элементы. В десятичном коде это 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; в двоичном — 0 и 1. Двоичный код проще десятичного и легче реализуется в технических системах. Поэтому он получил преимущественное распространение.
Любое число в двоичной системе счисления записывается в виде суммы
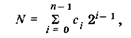
где с, — цифры двоичной системы счисления (0 или 1), стоящие в соответствующих разрядах; п — число разрядов. Правила суммирования в двоичной системе чрезвычайно просты:
0+0=0; 0+1=1; 1+0=1; 1+1= 10. Примеры приведены в табл. 51. Так, в частности, число 13 в двоичной системе записывается 1101, что соответствует сумме 1·23 + 1·22 +0·21 +1·20.
Из приведенных в табл. 51 примеров видно, что кодовые комбинации (совокупность кодовых элементов) могут иметь одинаковую или неодинаковую длину. Соответственно различаются равномерные и неравномерные коды. Число знаков в кодовой комбинации, равное числу разрядов, определяет значность равномерного кода. Например, пятизначный код Бодо, предназначенный для кодирования букв алфавита, позволяет образовать не 16, как четырехзначный (см. табл. 51), а 32 кодовых комбинации одинаковой длины. Вообще же, максимальное число, кодируемое n- разрядным двоичным кодом,
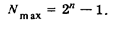
Уровни квантования совсем не обязательно должны кодироваться посредством их нумерации в двоичной системе счисления. В этом случае при переходе сигнала на соседний уровень возможно изменение двоичных кодовых элементов сразу в нескольких разрядах. Это повышает вероятность ошибок, называемых ошибками считывания. Во избежание этих ошибок применяются правила образования кодовых комбинаций, при которых соседние комбинации могут отличаться цифрой только в одном разряде. Такие коды получили название отраженных. Наиболее распространенным из них является код Грея (см. табл. 51), который легко преобразуется в двоичный код по следующему правилу: первая единица со стороны старших разрядов остается без изменения; последующие цифры остаются без изменения, если число единиц слева четно, и инвертируются — если нечетно.
Очень широкое распространение получило двоичное кодирование каждой цифры десятичного числа в отдельности. Так как цифр всего 10, то для этого необходимы 10 кодовых комбинаций, 3-х значный двоичный код позволяет образовать их 8, а 4-х значный — 16. Таким образом, первый не годится, а второй дает 6 лишних комбинаций. Так как в качестве лишних могут рассматриваться любые 6 из 16 возможных 4-х значных комбинаций, то открывается возможность построения большого числа самых разнообразных кодов. Они называются двоично-десятичными, причем в названии указываются коэффициенты, на которые нужно умножать соответствующие кодовые элементы для того, чтобы в сумме получалась кодируемая цифра. Так, при использовании кода 4—2—2—1 число 138 будет закодировано в виде 0001 0011 1110, что означает
4·0+2·0+2·0+1·1= 1;
4·0+2·0+2·1+1·1=3;
4·1+2·1+2·1+1·0=8.
Пример использования этого кода приведен в табл. 51. Как можно заметить, такое кодирование является неоднозначным. Цифра 3 может быть закодирована в виде 0101, цифра 4 — в виде 1000, 5 — в виде 1001 и т.д. Необходимая однозначность достигается только соответствующим построением устройств кодирования и декодирования. Единственным однозначным двоично-десятичным кодом является код 8 - 4 -2-1.
Общее число кодовых комбинаций, которое можно образовать с помощью п-разрядного двоичного кода, составляет
Nкк=2n
Если все они используются для кодирования измерительной информации, то код называется простым (примитивным). В простых равномерных кодах непреднамеренное изменение одного из кодовых элементов на противоположный приводит к возникновению новой комбинации, т.е. к ошибке. Коды, позволяющие обнаруживать и исправлять ошибки, называются корректирующими.
В корректирующих кодах в кодовые комбинации вводят дополнительные (избыточные) кодовые элементы. Длина кодовых комбинаций (число разрядов) увеличивается, но не все разряды используются для кодирования информации. Число информационных разрядов k определяет мощность
| и избыточность |
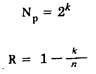
кода. Дополнительные разряды (их называют проверочными) служат для обнаружения и исключения ошибок.
Пример 79. Считая многократные ошибки (в нескольких разрядах) маловероятными, построить корректирующий код на базе кода Бодо.
Решение. Введем в код Бодо шестой (проверочный) разряд и будем заполнять его кодовыми элементами так, чтобы число единиц в каждой кодовой комбинации было четным. Тогда при появлении в результате помех или сбоев в аппаратуре кодовых комбинаций с нечетным числом единиц можно будет утверждать, что в них вкралась ошибка.
В рассмотренном примере корректирующий код позволяет обнаружить кодовые комбинации, в которых содержатся однократные или нечетной кратности ошибки, но не позволяет указать, в каком именно разряде. Для решения этой более сложной задачи требуется введение большего числа проверочных разрядов. Рассмотрим эту процедуру на примере построения кода Хэмминга, реализующего идею многократных проверок на четность различных вариантов сумм кодовых элементов в определенных разрядах кодовой комбинации. В результате таких проверок удается получить номер искаженного разряда в двоичной системе счисления.
Порядок построения кода Хэмминга следующий.
1. Определяется необходимое количество информационных k и проверочных т разрядов. Число проверок в дальнейшем будет равняться числу проверочных разрядов r , а результат каждой проверки будет обозначаться символом 0 или 1. Записанные справа налево символы образуют число в двоичной системе счисления, соответствующее номеру искаженного разряда. Так как это число не может быть меньше k, а число разрядов в нем равно r, то должно выполняться условие
R—1≥ k.
2. Все проверки заключаются в вычислении суммы по модулю 2 кодовых элементов в соответствующих разрядах кодовой комбинации. При первой проверке выбираются те разряды, двоичный номер которых содержит единицу в первом разряде, т.е. 1, 3, 5, 7, 9-й ... . При второй проверке выбираются разряды, двоичный номер которых содержит 1 во втором разряде, т.е. 2, 3, 6, 7, 10-й ... . При третьей проверке выбираются 4, 5, 6, 7,12,13-й . . . разряды и т.д.
3. Место расположения проверочных разрядов в кодовой комбинации в принципе может быть выбрано произвольным, однако при выбранном правиле проверок проверочные символы (0 или 1) удобнее размещать в разрядах, номера которых равны целой степени числа 2, т.е. в 1, 2, 4, 8-м и т.д.
4. Способ заполнения проверочных разрядов определяется правилом проверки корректирующего кода.
Пример 80. Построить код Хэмминга для чисел от 0 до 15 и воспользоваться им для коррекции кодовой комбинации.
Решение. 1. Так как Np = 16, то необходимое число информационных разрядов k = 4.
2. Исходя из условия 2r— 1 ≥k, необходимое число проверочных разрядов r = 3. Ход Хэмминга, следовательно, должен иметь п = k + r = 7 разрядов.
3. В соответствии с рекомендацией 3 в качестве проверочных удобно выбрать 1, 2 и 4-й разряды. Остальные (информационные) должны использоваться для размещения в них чисел от 0 до 15 в двоичной системе счисления.
4. После заполнения кодовыми элементами информационных и проверочных разрядов получим следующую кодовую таблицу:
Десятичное Кодовая
число комбинация
0 0000000
1 1101001
2 0101010
3 1000011
4 1001100
5 0100101
6 1100110
7 0001111
8 1110000
9 0011001
10 1011010
11 0110011
12 0111100
13 1010101
14 0010110
15 1111111
5. Рассмотрим кодовую комбинацию 0111110. В кодовой таблице ее нет, так что в одном из разрядов допущена ошибка (возможностью многократных ошибок по-прежнему будем пренебрегать). Первая проверка дает 0Å1Å1Å0=0; вторая —1Å1Å1Å0= 1; третья — 1Å1Å1Å0=1. Записывая результаты проверок, справа налево, устанавливаем, что искажен кодовый элемент в 110 (шестом) разряде. Таким образом, правильной является кодовая комбинация 0111100, соответствующая числу 12.
Использование избыточности и применение корректирующих кодов лежит в основе помехоустойчивого кодирования и обеспечения достоверности измерительной информации при передаче ее по дискретным каналам связи.
Во многих случаях, кроме того, большое значение имеет скорость передачи измерительной информации. Для ее повышения можно отказаться от избыточных кодовых элементов (нулей слева от первой единицы) в каждой кодовой комбинации. Код будет тогда неравномерным. Самыми короткими кодовыми комбинациями нужно закодировать наиболее вероятные значения сигнала, т.е. кодирование должно основываться на учете его статистических закономерностей. Критерием эффективности кода является средняя длина кодовой комбинации
lcp= åkPklk ,
где суммирование производится по всем кодируемым значениям сигнала; Pk — вероятность k-гo значения, a lk¾длина (число разрядов) соответствующей ему кодовой комбинации. Наиболее экономичным (эффективным) является код, средняя длина кодовой комбинации у которого минимальна. Такой код, синтезированный по критерию
åkPklk = min,
называется оптимальным. Он обеспечивается максимальную скорость передачи измерительной информации.
Первые методики построения оптимальных кодов были предложены К. Шенноном и Р.Фэно. Они существенно не отличаются, и соответствующий код получил, поэтому название кода Шеннона-Фэно. Порядок построения этого кода рассмотрим на примере.
Пример 81. В дискретный канал связи измерительной системы поступает сигнал от промежуточного измерительного преобразователя, подчиняющийся нормированному нормальному закону распределения вероятности. Измерительная информация содержится в корреляционной функции сигнала. Построить код Шеннона-Фэно для передачи значений сигнала после его дискретизации.
Решение. 1. Сигнал Х (t) в каждый момент времени характеризуется уровнем квантования, который может быть положительным или отрицательным. Разобьем сначала весь диапазон изменения сигнала на 10 равных поддиапазонов, ограниченных пятью положительными и пятью отрицательными уровнями. После этого поддиапазоны, прилегающие к нулевому уровню, дополнительно разобьем пополам. Получим всего 12 поддиапазонов. Вероятность того, что сигнал Х (t) окажется в одном из поддиапазонов, равна разности значений функции Лапласа на границах поддиапазона. Например, вероятность того, что сигнал Х (t) окажется в поддиапазоне между 4-м и 5-м уровнями, равна L (5) — L (4) ≈ 0,001, между 1-м и 2-м -L (2) -L (1) ≈ 0,136,между уровнями 0 и 1/2 - L (-1/2)-L (0) ≈0,192, между уровнями -1 и -1/2 - L (-1/2) -L (-1) ≈0,149 и т.д. Все сформированные под
диапазоны и вероятности того, что сигнал Х (t) окажется в каждом из них, приведены в порядке убывания в табл.52.
2. При построении кода Шеннона-Фэно все возможные варианты сначала делятся на две группы так, чтобы суммы вероятностей в каждой изних были по возможности одинаковы (см. табл. 52). Всем вариантам I группы в качестве первого символа в кодовой комбинации приписывается 0 а вариантам II группы - I. Затем каждая группа в свою очередь разбивается на две подгруппы с примерно одинаковыми суммарными вероятностями, процедура присвоения символов повторяется и т.д.
Кодовая таблица для рассматриваемого примера представлена первой и последней графами в табл. 52.
Таблица 52
| Поддиапазон между уровнями | Вероятность попадания сигнала в поддиапазон | Деления на группы | Кодовая комбинация | ||||||||||||||||||||||||||||||||||||||||||||||
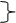 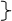                     0 . . . 0,5 0 . . . 0,5
0 . . . – 0,5
0,5 . . . 1
- 0,5 . . . - 1
1 . . . 2
- 1 . . . - 2
2 . . . 3
-2 . . . - 3
3 . . . 4
- 3 . . . - 4
4 . . . 5
- 4 . . . - 5 | 0,192 0,192 0,149 0,149 0,136 0,136 0,021 0,021 0,001 0,001 0,001 0,001 |
Дата добавления: 2015-02-05; просмотров: 2760;
