Спектр одиночного прямоугольного импульса
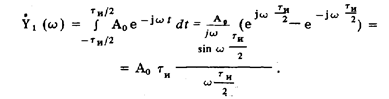
Графическое изображение его представлено на рис. 92b Спектр является бесконечным и имеет нули при частотах 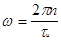 . Под реальной шириной спектра понимают полосу частот, ограниченную первым лепестком. Эта полоса частот тем больше, чем меньше длительность импульса.
. Под реальной шириной спектра понимают полосу частот, ограниченную первым лепестком. Эта полоса частот тем больше, чем меньше длительность импульса.
Спектральный состав последовательности прямоугольных импульсов можно получить, разложив функцию Y0{t), показанную на рис. 172, в ряд Фурье: 
Спектр амплитуд, соответствующий этому выражению, приведен на рис. 94. Он линейчатый (дискретный) с расстояниями между линиями 1/Т. Рассмотрев дискретные значения частоты w = п w1, можно заметить, что амплитуды соответствующих спектральных составляющих определяются выра жением
çsinw(tИ /2)ê
————————,
w(tИ /2)
которое описывает спектр амплитуд одиночного прямоугольного импульса. Поэтому график спектра амплитуд одиночного импульса является огибающей спектра амплитуд периодической последовательности импульсов, а реальная ширина спектра периодической последовательности определяется длительностью импульсов. Она тем больше, чем меньше длительность импульса.
Влияние модуляции на спектральный состав последовательности прямоугольных импульсов рассмотрим на примере АИМ. Пусть, по-прежнему,
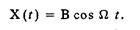
Амплитуда импульсов в этом случае меняется по закону
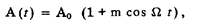
где m = 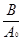 £1 — глубина модуляции. Амплитудно-модулированная последовательность прямоугольных импульсов
£1 — глубина модуляции. Амплитудно-модулированная последовательность прямоугольных импульсов
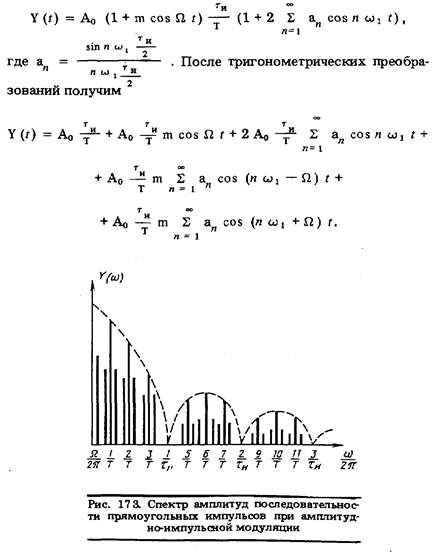
Соответствующий спектр амплитуд при скважности, равной 4, изображен на рис. 173. Кроме основных линий, содержащихся в спектре немодулированной последовательности прямоугольных импульсов, имеются боковые линии, распо-ложенные по обе стороны от основных на расстоянии 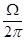 .
.
Амплитуды этих боковых линий в 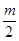 раз меньше амплитуд основных линий спектра.
раз меньше амплитуд основных линий спектра.
При ЧИМ, ШИМ и ФИМ даже при простейшей гармонической модуляции (как в рассмотренном примере) вокруг каждой основной линии спектра располагается бесконечное множество боковых линий, однако их амплитуды быстро убывают. Таким образом, любая импульсная модуляция усложняет спектр периодической последовательности прямоугольных импульсов, но ширина его при этом остается такой же, как у одиночного импульса.
Кодово - импульсная модуляция. При передаче закодированной измерительной информации по дискретным каналамсвязи применяется кодово-импульсная модуляция. Иногда ее называют манипуляцией, а соответствующие устройства (модуляторы или манипуляторы) — модемами.
Как и в предыдущем случае, кодово-импульсная модуляция может быть амплитудной (AM), частотной (ЧМ), и фазовой (ФМ).
На рис. 174 приведены временные диаграммы, иллюстрирующие различные виды манипуляции. При AM кодовому элементу 1 соответствует передача несущего колебания в течение времени Т (посылка), кодовому элементу 0 — отсутствие колебания (пауза). При ЧМ передача несущего колебания с частотой w1 соответствует кодовому элементу 1, а передача колебания с частотой w0 — элементу 0. При двоичной ФМ меняется фаза несущей на т при каждом переходе от 1 к 0 и от 0 к 1.
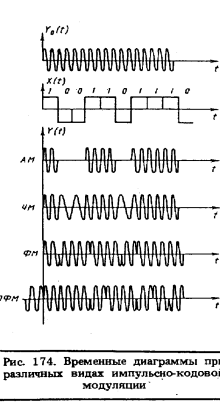 Наконец, на практике нашла применение относительная фазовая модуляция (ОФМ). В отличие от ФМ, при ОФМ фаза несущего колебания отсчитывается не от начальной фазы, а от фазы предыдущего элемента сигнала. В двоичном случае символ 0 передается отрезком синусоиды с начальной фазой предшествующего элемента сигнала, а символ 1 — таким же отрезком с начальной фазой, отличающейся на p от фазы предыдущего элемента сигнала. Начинается передача при ОФМ с посылки одного, не несущего информации элемента, фаза которого является опорной для сравнения с ней фазы последующего элемента.
Наконец, на практике нашла применение относительная фазовая модуляция (ОФМ). В отличие от ФМ, при ОФМ фаза несущего колебания отсчитывается не от начальной фазы, а от фазы предыдущего элемента сигнала. В двоичном случае символ 0 передается отрезком синусоиды с начальной фазой предшествующего элемента сигнала, а символ 1 — таким же отрезком с начальной фазой, отличающейся на p от фазы предыдущего элемента сигнала. Начинается передача при ОФМ с посылки одного, не несущего информации элемента, фаза которого является опорной для сравнения с ней фазы последующего элемента.
В более общем случае кодово-импульсную модуляцию следует рассматривать, как преобразование кодовых элементов в определенные отрезки несущей причем вид последней может быть произвольным. В том числе это может быть и периодическая последовательность импульсов прямоугольной или любой другой формы. На практике Yo (t) выбирают таким образом, чтобы удовлетворить требованиям, предъявляемым к системе связи (в частности, по скорости передачи и по занимаемой полосе частот), и чтобы сигналы хорошо раз- личались на фоне помех.
Длительность посылки при кодово-импульсной модуляции определяет скорость передачи измерительной информации. Эта скорость выражается числом посылок в единицу времени и измеряется в бодах. Один бод равен скорости передачи, при которой за 1с передается одна посылка.
Если длительность посылки выражена в секундах, то скорость телеграфирования с = 1/Т бод. Частота манипуляции не превышает Fм = 1/2 Т = с/2 Гц. Если полосу частот Х (t) ограничить третьей гармоникой, то с шириной спектра модулирующего сигнала Fc скорость передачи будет связана соотношением
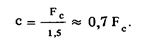
Дата добавления: 2015-02-05; просмотров: 4798;
