Декодерами в измерительных системах являются преоб­разователи код—код.

Приведение измерительной информа­ции к виду, удобному для дальнейшей переработки, рассмотрим на примере преобразования кода Грея, непригодного для вычислительных операций, в дво­ичный код.

Преобразователь состоит из генератора тактовых импуль­сов ГИ (см. рис. 181) и триггера Тг, который управляется

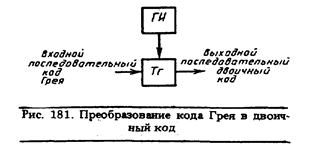
импульсами кода Грея. Для преобразования используется совпадение знаков старшего разряда у кода Грея и у обыч­ного двоичного кода. Последовательность работы преобра­зователя поясняется на примере преобразования числа 8 в коде Грея 1100 в число 8 в двоичном коде 1000:

Тактовые импульсы Импульсы кода Грея, управляющие нор­мально закрытым триггером Состояние триггера Импульсы двоичного кода на выходе схемы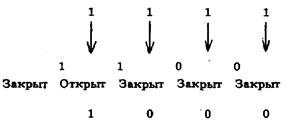

Первый импульс кода Грея старшего разряда открывает закрытый триггер, и первый тактовый импульс проходит на выход, образуя импульс старшего разряда двоичного ко­да. Второй импульс кода Грея закрывает триггер, который остается в дальнейшем закрытым, т.к. в остальных двух младших разрядах числа 8 по коду Грея импульсов нет. Поэтому все остальные тактовые импульсы через .закрытый триггер не проходят, и на выходе получается двоичный после­довательный код числа 8.

Приведение измерительной, информа­ции к виду, удобному для восприятия че­ловеком в цифровой форме, рассмотрим на примере преобразования семиразрядного кода Хэмминга (см. пример 80) в десятичный код.

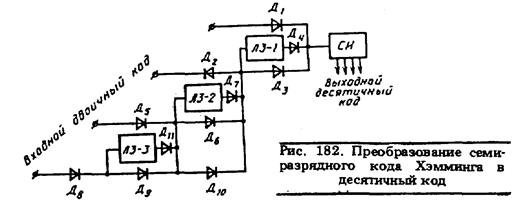
Схема, поясняющая принцип действия преобразователя, приведена на рис. 182. Работа устройства основана на преоб­разовании импульсов, поступающих по каналам, соответст­вующим информационным разрядам кода Хэмминга, в пачки импульсов. Число импульсов в пачке равно числу двоичных единиц в разряде. Пачки импульсов поступают в счетчик им­пульсов СИ, в котором импульсы подсчитываются и резуль­тат выдается в десятичной системе счисления.

Рассмотрим преобразование кодовой комбинации 0110011 в семиразрядном коде Хэмминга, построенном в примере 80; в десятичный код.

Импульс, соответствующий 1 в младшем информацион­ном разряде, через диод Д₁ поступает в счетчик импульсов СИ. Импульс, соответствующий 1 в следующем разряде, прев­ращается в пачку из двух импульсов. Первый изних через диоды Д₂ и Д₃ проходит в счетчик непосредственно, а второй, образующийся на выходе линии задержки ЛЗ-1, следует за ним через диод Д₄ с запаздыванием по времени на Dt. В следующем информационном разряде стоит 0, поэтому через диод Д₅ импульс в схему не поступает. Затем следует прове­рочный разряд, не подключенный к преобразователю. В стар­шем информационном разряде стоит 1. Соответствующий импульс превращается в пачку из 8 импульсов следующим об­разом. Через диоды Д₈, Д₉, Д₁₀ и Д₃ он проходит в счетчик непосредственно. Заним через диод Д₄ следует импульс, за­держанный на Dt. Сформировавшийся на выходе линии за­держки ЛЗ-2 импульс запаздывает на 2Dt .Он опять-таки превращается в два импульса, первый из которых через диоды Д₇ и Д₃ поступает в счетчик непосредственно, а второй, обра­зующийся на выходе линии задержки ЛЗ-1, следует за ним через диод Д₄ с запаздыванием по времени на Dt. По отно­шению к самому первому импульсу он запаздывает, следова­тельно, уже на 3Dt. Импульс, сформировавшийся на выходе линии задержки ЛЗ-3, запаздывает по отношению к первому на 4 Dt. Он превращается в 4 импульса, первыйиз которых поступает в счетчик непосредственно через диоды Д₁₁,Д₆ и Дз, второй — с выхода линии задержки ЛЗ-1 через диод Д₄ третий — с выхода линии задержки ЛЗ-2 через диоды Д₇ и Д₃ и четвертый, с формировавшийся из предыдущего после задержки на время Dt в линии задержки ЛЗ-1, — через диод Д4 . Таким образом, показание счетчика в десятичной сис­теме счисления будет равно 11, что соответствует кодовой таблице, приведенной в примере 80.

Если измерительная информация дол­жна быть представлена в аналоговой форме, то возникает задача восстановления непрерыв­ного сигнала (см. рис. 162, а) по ряду его дискретных зна­чений (рис. 162, б). Если дискретизация была выполнена в соответствии с теоремой В.А. Котельникова, то наиболее просто эта задача решается с помощью низкочастотного фильтра. Функция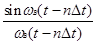

является откликом идеальногонизкочастотного фильтра на единичный импульс. Для восста­новления сигнала Х(t) (см. рис. 163) необходимо подавать на вход фильтра с верхней граничной частотой w_B последо­вательность коротких импульсов с амплитудами, равным мгновенным значениям сигнала в соответствующие моменты времени. Тогда на нагрузке будут суммироваться члены ряда В.А. Котельникова (см. рис. 163), обеспечивая тем самым восстановление сигнала. Качество восстановления естест­венно, будет зависеть от соблюдения множества условий, таких как правильный выбор шага квантования по времени Dt, точность воспроизведения в импульсном режиме мгно­венных значений сигнала, близость амплитудно-частотной характеристики фильтра к прямоугольной, а фазочастотной — к линейной и мн. др.

Если условия теоремы В.А. Котельникова не выполняются (например, квантование по времени выполнено с неравномер­ным шагом), то в качестве воспроизводящих используются другие функции. С одной стороны они должны обеспечи­вать необходимую точность воспроизведения сигнала при минимальном числе членов разложения, а с другой — допус­кать возможность простой технической реализации. Послед­нему требованию удовлетворяют прежде всего степенные полиномы.

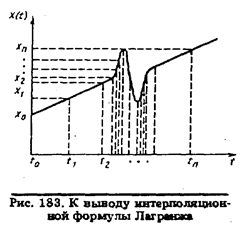Задача - восстановления сигнала с помощью поли­нома n-й степени ставится следующим образом. Пусть известны значения сигнала C₀, X₁, Х₂ , . .. Х_n в момен­ты времени t₀ ,t₁ ,t₂ , ... , t_n (см. рис. 183). Требуется найти такой непрерывный сигнал Х(t), который в моменты времени t_j прини­мал бы значения X_J .

Найдем прежде всего непрерывную функцию, принимающую значение 1 в момент времени t₀, и рав­ную нулю во все остальные моменты времени t_i. Легко проверить, что такой функцией будет дробь

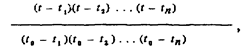
в которой при t = t₀ числитель и знаменатель оказываются совершенно идентичными, а в любой другой момент време­ни t_i, один из сомножителей в числителе обращается в ноль. Домножив эту функцию на Х₀, получим непрерывный сиг­нал

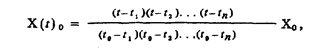
принимающий значение Х₀ в момент времени t₀ , и равный нулю во все остальные моменты времени t_i .

Поступая по аналогии, можно сформировать сигналы

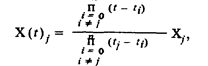
принимающиезначения X_j в моменты времени t_j, и равные нулю во все остальные дискретные моменты времени t_i ≠ t_j . Искомый сигнал Х(t) будет равен сумме этих сиг­налов

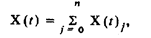
так как в каждый из моментов времени t_j принимает значе­ние X_j.

Формула

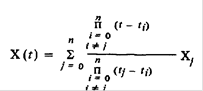
называется интерполяционной формулой Лагранжа и пред­ставляет собой полином n-й степени. На практике обычно интерполируют сигнал между двумя соседними дискретными значениями. В этом случае п = 1, и интерполяционный поли­номимеет вид

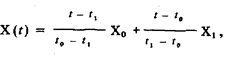
или, после преобразований,

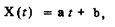
где а = 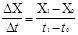; b= . Это уравнение прямой,

проходящей через точки с координатами (t₀,Xо) и (t₁,Xi). Такая интерполяция называется линейной. Пример восста­новления сигнала методом линейной интерполяции показан на рис. 184.

При степени полинома п = 0 интерполяция фактически превращается в экстраполяцию, так как в этом случае

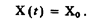
Пример восстановления сигнала таким способом в каждый дискретный момент времени t_j .показан на рис. 185. В изме­рительной технике этот способ восстановления реализует­ся с помощью разнообразных преобразователей код—аналог.