Погрешности измерений. Всякое измерение, как бы тщательно оно ни проводилось, дает лишь приближенный результат и не может не содержать ошибок (погрешностей измерения).
Всякое измерение, как бы тщательно оно ни проводилось, дает лишь приближенный результат и не может не содержать ошибок (погрешностей измерения).
Пусть произведено n измерений некоторой физической величины х, в результате которых получен ряд значений этой величины: х1, х2, …, хn. Выполнив измерения, необходимо привести не только полученный результат, но и дать информацию о его точности. В подавляющем большинстве случаев наилучшей оценкой величины х, основанной на измерениях значений х1, х2, …, хn, является среднее арифметическое результатов измерений <x>. При этом необходимо указывать интервал значений измеряемой величины +Dх, в пределах которого с определенной вероятностью может оказаться истинное значение измеряемой величины: <х> + Dх есть наибольшее вероятное значение измеряемой величины, <х>-Dх – наименьшее.
Величина Dх называется погрешностью или ошибкой результата, интервал от <х>+Dх до <х>-Dх – доверительным интервалом. Вероятность того, что среднее значение <х> отличается от истинного не более, чем на Dх – называется доверительной вероятностью Р.
Она равна доле результатов однотипных серий измерений, попадающих в пределы доверительного интервала, т.е. отличающихся от истинного значения не более, чем на Dх. Обычно ошибки измерения находятся для определенной вероятности Р0. Для обеспечения более надежного совпадения измеренного результата с истинным значением величины может быть введена большая вероятность Р. В этом случае устанавливается доверительный интервал с границами +e = kDх, где коэффициент k определяется отношением Р/Р0. Доверительные границы e определяются по заданной вероятности Р того, что на числовой оси отрезок 2e с центром в точке <х> включает значение измеряемой величины х.
Если в результаты измерений введены все известные поправки к показаниям приборов и устранены грубые ошибки или промахи, то среднее арифметическое исправленных результатов измерений вычисляется по формуле:
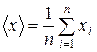
Обычно в качестве общепринятой стандартной погрешности измерения принимается среднеквадратичная ошибка. Она равна дисперсии распределения Гаусса для случайных величин, которое считается хорошим приближением к распределению ошибок измерения.
Среднее квадратичное отклонение среднего арифметического результата измерения
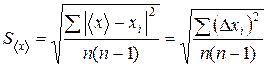
Среднее квадратичное отклонение S<x> характеризует погрешность среднеарифметического <x>. Запись в виде х = + S<x> означает, что в 68 % случаев результаты любых последующих измерений <x>, выполненных с такой же тщательностью, попадут в интервал (<x>-S<x> , <x>+S<x>). Другими словами, полученный результат будет находится в пределах ±S<x> от правильного результата с доверительной вероятностью Р=68 %. Вероятность того, что результат измерения окажется в пределах +2S<x> равна 95,4%; в пределах +3S<x> - 99,7%.
Распределение ошибок измерения совпадает с распределением Гаусса только при бесконечно большом числе измерений. При конечном числе измерений вычислить доверительные границы случайной погрешности результата измерения можно при помощи так называемого распределения Стьюдента
e = + tp,n S<x>
где +tp,n – коэффициент Стьюдента для числа наблюдений n и доверительной вероятности Р, определяемый по таблице коэффициентов Стьюдента.
Таблица коэффициентов Стьюдента
Р – доверительная вероятность, n – число измерений
| n\P | 0,5 | 0,6 | 0,7 | 0,8 | 0,09 | 0,95 | 0,0989 | 0,999 |
| 0,82 0,77 0,74 0,73 0,72 0,71 0,71 0,70 0,69 0,69 0,68 0,68 0,68 0,67 | 1,38 1,06 0,98 0,94 0,92 0,90 0,90 0,90 0,88 0,87 0,86 0,85 0,85 0,85 0,84 | 2,0 1,3 1,3 1,2 1,2 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,0 1,0 1,00 | 3,1 1,9 1,6 1,5 1,5 1,4 1,4 1,4 1,4 1,3 1,3 1,2 1,3 1,3 1,3 | 6,3 2,9 2,4 2,1 2,0 1,9 1,9 1,9 1,8 1,8 1,7 1,7 1,7 1,7 1,6 | 12,7 4,3 3,2 2,8 2,6 2,4 2,4 2,3 2,3 2,1 2,1 2,0 2,0 2,0 2,0 | 31,8 7,0 4,5 3,7 3,4 3,1 3,00 2,9 2,8 2,6 2,5 2,4 2,4 2,4 2,3 | 636,6 31,6 12,9 8,6 6,9 6,0 5,4 5,0 4,8 4,1 3,9 3,6 3,5 3,4 3,3 |
Как видно из таблицы уже при числе измерений 5-10 можно пользоваться среднеквадратичной ошибкой как и при бесконечно большом числе измерений. При автоматизированных измерениях число измерений может быть очень большим, однако увеличение числа измерений приводит лишь к уменьшению среднеквадратичной ошибки и не изменяет доверительной вероятности в пределах интервала этих ошибок.
Ошибки можно разделить на два типа: систематические и случайные. Основное различие между ними заключается в том, что систематические погрешности остаются постоянными по величине и знаку; случайные погрешности, наоборот, непредсказуемым образом изменяют свою величину и знак. Случайные погрешности можно уменьшить с помощью многократных измерений. Систематические ошибки таким способом уменьшить нельзя. Случайные погрешности можно обрабатывать статистическими методами, к систематическим погрешностям эти методы неприменимы.
Систематические ошибки возникают вследствие погрешностей измерительной аппаратуры (отстающий секундомер, вытянутая линейка, стрелочный прибор, у которого стрелка до начала измерений не была установлена на нуль). А также отличием условий эксперимента от предполагаемых теорией, несовершенства методики эксперимента. Общих правил для определения систематических ошибок не существует; в каждом конкретном случае их выявление требует специальных исследований. Полностью исключить систематические ошибки нельзя, можно лишь перевести их в разряд случайных.
Случайные ошибки всегда присутствуют в эксперименте и являются результатом суммарного действия большого количества факторов, влияние каждого из которых в отдельности учесть практически невозможно. Типичные источники случайных погрешностей: небольшие ошибки наблюдателя, небольшие помехи, воздействующие на аппаратуру и другие. Случайные погрешности нельзя исключить, но их влияние можно учесть с помощью многократных измерений с последующей математической обработкой результатов измерений.
Разновидность случайных ошибок - грубые ошибки или промахи. Они возникают вследствие невнимательности экспериментатора (например, неправильные отсчеты по прибору, неправильная запись отсчета и т.п.). В большинстве случаев при многократных измерениях промахи хорошо заметны, так как соответствующие им отсчеты сильно отличаются от других. При обработке результатов такие отсчеты следует отбрасывать.
Доверительные границы общей погрешности результата измерения с учетом систематической погрешности
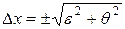
где q - систематическая погрешность, которая в условиях учебной лаборатории оценивается по цене деления шкалы или указывается на приборе. В некоторых случаях доверительные границы общей погрешности рассчитывается по формуле.
Dx=± 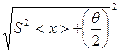
Окончательный результат измерения записывается в виде
х=<x>±Dx;
Например, ρ = (7,70±0,72)*103кг/м3, Р=0,95.
Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и первая значащая цифра доверительных границ Dx. Доверительные границы записываются с двумя значащими цифрами.
Относительная погрешность результата измерения, характеризующая точность измерений.
s= 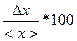 %
%
Дата добавления: 2015-02-03; просмотров: 933;
